Chapter 3.9, Problem 93E

Logistic growth Scientists often use the logistic growth function $P(t)=\frac{P_{0}K}{P_0+(K-P_0)e^{-r_{0}t}}$to model population growth, where P₀ is the initial population at time t = 0, K is the carrying capacity, and r₀ is the base growth rate. The carrying capacity is a theoretical upper bound on the total population that the surrounding environment can support. The figure shows the sigmoid (S-shaped) curve associated with a typical logistic model.

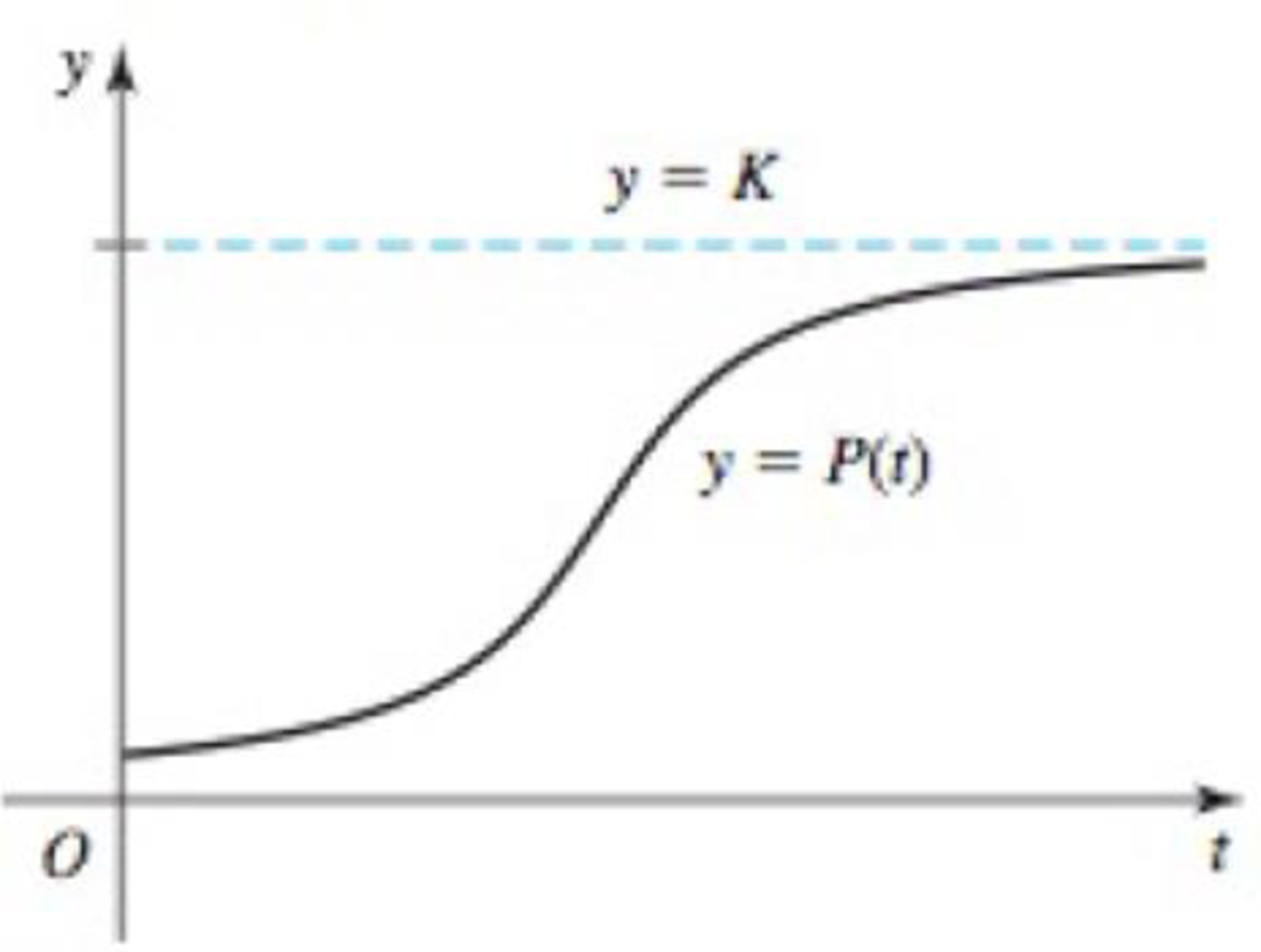
93. Gone fishing When a reservoir is created by a new dam, 50 fish are introduced into the reservoir, which has an estimated carrying capacity of 8000 fish. A logistic model of the fish population is $P(t)=\frac{400,000}{50+7950e^{-0.5t}}$, where t is measured in years.

1. a. Graph P using a graphing utility. Experiment with different windows until you produce an S-shaped curve characteristic of the logistic model. What window works well for this function?
2. b. How long does it take the population to reach 5000 fish? How long does it take the population to reach 90% of the carrying capacity?
3. c. How fast (in fish per year) is the population growing at t = 0? At t = 5?
4. d. Graph P’ and use the graph to estimate the year in which the population is growing fastest.