
Laplace Transforms
In the last few chapters, we have looked at several ways to use
The Laplace transform is defined in terms of an integral as
7
e""
ft
Note that the input to a Laplace transform is a function of time, /(/), and the output is a function of frequency, F(j), Although many real-world examples require the use of
Let's stan with a simple example. Here we calculate the Laplace transform of /(f) = t. We have
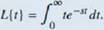
This is an improper integral, so we express it in terms of a limit, which gives
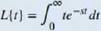
Now we use integration by pans to evaluate the integral. Note that we are integrating with respect to t, so we treat the variable s as a constant. We have
u—t dv — dt
du=dt v
— — ye_ir.
Then we obtain
= + +
= ~K + °1 -
= JinL[[-i,-]-±[e--lj]
- c + c
= 0-0 + -L
s“
_x
2* s
1. Calculate the Laplace transform of /(/) = 1.
3.Calculate the Laplace transform of /(/) = : (Note, you will have to integrate by parts twice.)
Laplace transforms are often used to solve differential equations. Differential equations are not covered in detail until later in this book; but, for now, let’s look at the relationship between the Laplace transform of a function and the Laplace transform of its derivative.
Let’s start with the definition of the Laplace transform. We have
WW! = r™ r'
= lim / e~st fifth.
4.Use integration by parts to evaluate Jjm^ e~sl fifth. (Let « = /{/) and dv — e '!dt.) After integrating by parts and evaluating the limit, you should see that
Then,
Thus, differentiation in the time domain simplifies to multiplication by s in the frequency domain.
The final thing we look at in this project is how the Laplace transforms of fit] and its antiderivative are
related. Let g(r) — f(u}dii. Then,
¦'o
lim /
;-* caj" 5.Use integration by parts to evaluate hrn^y e ’ g(t)dl. (Let u = gif) and dv = e dt. Note, by the way,
that we have defined gif, du — fifth.)
As you might expect, you should see that
L|^(r)| = |-L[/(/)i.
Integration in the time domain simplifies to division by s in ±e frequency domain.
Want to see the full answer?
Check out a sample textbook solution
Chapter 3 Solutions
Calculus Volume 2
Additional Math Textbook Solutions
Thinking Mathematically (6th Edition)
Elementary Statistics (13th Edition)
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
A First Course in Probability (10th Edition)
Elementary Statistics: Picturing the World (7th Edition)
- 5) For each function represented by an equation, make a table and plot the corresponding points to sketch the graph of the function. (a) y = 75 ()* 220 X y 200- -2 180 160 -1 140 0 120 100 1 60 80 2 3 4 x (b) y = 20 ()* 1 60 40 20 20 0 2 3 65- -1 X y 60 -2 55- 50 45 44 40 0 35- 30 1 25 2 20 20 15 3 10 5 LO 4 3-2 T -1 0 5- 4- -3- 2-arrow_forward5. Find the solution to each of the following by using an appropriate formula developed in the lecture slides: (a) + 3y = 2, y(0) = 4; (b) dy - 7y = 7, y(0) = 7; (c) 3d+6y= 5, y(0) = 0arrow_forward1. Evaluate the following improper integrals: (a) fe-rt dt; (b) fert dt; (c) fi da dxarrow_forward
- 8. Given the rate of net investment I(t) = 9t¹/2, find the level of capital formation in (i) 16 years and (ii) between the 4th and the 8th years.arrow_forward9. If the marginal revenue function of a firm in the production of output is MR = 40 - 10q² where q is the level of output, and total revenue is 120 at 3 units of output, find the total revenue function. [Hints: TR = √ MRdq]arrow_forward6. Solve the following first-order linear differential equations; if an initial condition is given, definitize the arbitrary constant: (a) 2 + 12y + 2et = 0, y(0) = /; (b) dy+y=tarrow_forward
- 4. Let A = {a, b, c, d, e, f}, B = {e, f, g, h} and C = {a, e, h,i}. Let U = {a, b, c, d, e, f, g, h, i, j, k}. • Draw a Venn Diagram to describe the relationships between these sets Find (AB) NC • Find (AC) UB Find AUBUC • Find (BC) N (A - C)arrow_forward7. A consumer lives on an island where she produces two goods x and y according to the production possibility frontier x² + y² < 200 and she consumes all the goods. Her utility function is U(x, y) = x y³. She faces an environmental constraint on her total output of both goods. The environmental constraint is given by x + y ≤20. • (a) Write down the consumer's optimization problem. (b) Write out the Kuhn-Tucker first order conditions. (c) Find the consumer's optimal consumption bundle (x*, y*).arrow_forward3. Answer the following questions: (a) Given the marginal propensity to import M'(Y) = 0.1 and the information that M = 20 when Y = 0, find the import function M(Y). (b) Given a continuous income stream at the constant rate of $1,000 per year, what will be the present value II if the income stream terminates after exactly 3 years and the discount rate is 0.04? (c) What is the present value of a perpetual cash flow of $2,460 per year, discounted at r = 8%?arrow_forward
- 5. Let A and B be arbitrary sets. Prove AnB = AUB.arrow_forward2. Answer the following questions: (a) Given the marginal-revenue function R'(Q) = 28Q - €0.3Q, find the total-revenue function R(Q). What initial condition can you introduce to definitize the constant of integration? = (b) Given the marginal propensity to consume C'(Y) 0.80.1Y-1/2 and the information that C = Y when Y = 100, find the consumption function C(Y).arrow_forwardX GG G + C td.bksblive2.com.au/bksblive2/Play... E R New Chrome available CANVAS gmetrix N notion Six big immigratio... >>> All Bookmarks 1.1 ACSF L5 SC Geometry and Measure: Vectors Vectors State the vector quantities shown on the image below. AB = CD' = A B D < C 80 esc F1 F2 F3 F4 ? Help 7arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
