Linear Algebra: A Modern Introduction
4th Edition
ISBN: 9781285463247
Author: David Poole
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 3.7, Problem 54EQ
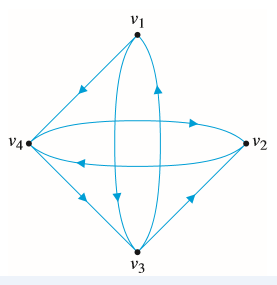
In Exercises 53-56, determine the adjacency matrix of the demand given digraph.
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
A research study in the year 2009 found that there were 2760 coyotes
in a given region. The coyote population declined at a rate of 5.8%
each year.
How many fewer coyotes were there in 2024 than in 2015?
Explain in at least one sentence how you solved the problem. Show
your work. Round your answer to the nearest whole number.
Answer the following questions related to the following matrix
A =
3
³).
Explain the following terms
Chapter 3 Solutions
Linear Algebra: A Modern Introduction
Ch. 3.1 - Let...Ch. 3.1 - Let
In Exercises 1-16, compute the indicated...Ch. 3.1 - Let...Ch. 3.1 - Let
In Exercises 1-16, compute the indicated...Ch. 3.1 - Let...Ch. 3.1 - Let
In Exercises 1-16, compute the indicated...Ch. 3.1 - Let
In Exercises 1-16, compute the indicated...Ch. 3.1 - Let...Ch. 3.1 - Let...Ch. 3.1 - Let...
Ch. 3.1 - Let
In Exercises 1-16, compute the indicated...Ch. 3.1 - Let
In Exercises 1-16, compute the indicated...Ch. 3.1 - Let...Ch. 3.1 - Let...Ch. 3.1 - Let...Ch. 3.1 - Let...Ch. 3.1 - Give an example of a nonzero 22 matrix A such that...Ch. 3.1 - Let A=[2613]. Find 22 matrices B and C such that...Ch. 3.1 - A factory manufactures three products (doohickies,...Ch. 3.1 - Referring to Exercise 19, suppose that the unit...Ch. 3.1 - In Exercises 21-22, write the given system of...Ch. 3.1 - In Exercises 21-22, write the given system of...Ch. 3.1 - In Exercises 23-28, let A=[102311201] and...Ch. 3.1 - In Exercises 23-28, let
and
24. Use the...Ch. 3.1 - In Exercises 23-28, let
and
25. Compute the...Ch. 3.1 - In Exercises 23-28, let A=[102311201] and...Ch. 3.1 - In Exercises 23-28, let
and
27. Use the...Ch. 3.1 - Prob. 28EQCh. 3.1 - In Exercises 29 and 30, assume that the product AB...Ch. 3.1 - Prob. 30EQCh. 3.1 -
In Exercises 31-34, compute AB by block...Ch. 3.1 - In Exercises 31-34, compute AB by block...Ch. 3.1 - In Exercises 31-34, compute AB by block...Ch. 3.1 - In Exercises 31-34, compute AB by block...Ch. 3.1 - Prob. 35EQCh. 3.1 - Let B=[12121212]. Find, with justification, B2015.Ch. 3.1 - Let A=[1101]. Find a formula for An(n1) and verify...Ch. 3.1 - 38. Let
(a) Show that
(b) Prove, by mathematical...Ch. 3.1 - In each of the following, find the 66matrixA=[aij]...Ch. 3.2 - In Exercises 1-4, solve the equation for X, given...Ch. 3.2 - In Exercises 1-4, solve the equation for X, given...Ch. 3.2 - In Exercises 1-4, solve the equation for X, given...Ch. 3.2 - In Exercises 1-4, solve the equation for X, given...Ch. 3.2 - In Exercises 5-8, write B as a linear combination...Ch. 3.2 - In Exercises 5-8, write B as a linear combination...Ch. 3.2 - In Exercises 5-8, write B as a linear combination...Ch. 3.2 - In Exercises 5-8, write B as a linear combination...Ch. 3.2 - In Exercises 9-12, find the general form of the...Ch. 3.2 - In Exercises 9-12, find the general form of the...Ch. 3.2 - In Exercises 9-12, find the general form of the...Ch. 3.2 - In Exercises 9-12, find the general form of the...Ch. 3.2 - In Exercises 13-16, determine whether the given...Ch. 3.2 - In Exercises 13-16, determine whether the given...Ch. 3.2 - In Exercises 13-16, determine whether the given...Ch. 3.2 - In Exercises 13-16, determine whether the given...Ch. 3.2 - 17. Prove Theorem 3.2(a) -(d).Ch. 3.2 - Prove Theorem 3.2 (e) (h).Ch. 3.2 - Prove Theorem 3.3(c).Ch. 3.2 - Prove Theorem 3.3(d).Ch. 3.2 - Prove the half of Theorem 3.3 (e) that was not...Ch. 3.2 - 22. Prove that, for square matrices A and B, AB =...Ch. 3.2 - In Exercises 23-25, if , find conditions on a, b,...Ch. 3.2 - In Exercises 23-25, if B=[abcd], find conditions...Ch. 3.2 - In Exercises 23-25, B=[abcd], find conditions on...Ch. 3.2 - 26. Find conditions on a, b, c, and d such that ...Ch. 3.2 - 27. Find conditions on a, b, c, and d such that ...Ch. 3.2 - Prove that if AB and BA are both defined, then AB...Ch. 3.2 - A square matrix is called upper triangular if all...Ch. 3.2 - 33. Using induction, prove that for all
.
Ch. 3.3 - In Exercises 1-10, find the inverse of the given...Ch. 3.3 - In Exercises 1-10, find the inverse of the given...Ch. 3.3 - In Exercises 1-10, find the inverse of the given...Ch. 3.3 - In Exercises 1-10, find the inverse of the given...Ch. 3.3 - In Exercises 5-8, write B as a linear combination...Ch. 3.3 - Prob. 6EQCh. 3.3 - In Exercises 1-10, find the inverse of the given...Ch. 3.3 - In Exercises 1-10, find the inverse of the given...Ch. 3.3 - In Exercises 1-10, find the inverse of the given...Ch. 3.3 - In Exercises 1-10, find the inverse of the given...Ch. 3.3 - In Exercises 11 and 12, solve the given system...Ch. 3.3 - In Exercises 11 and 12, solve the given system...Ch. 3.3 - Let A=[1226],b1=[35],b2=[12],andb3=[20]. Find A-1...Ch. 3.3 - In Exercises 20-23, solve the given matrix...Ch. 3.3 - In Exercises 20-23, solve the given matrix...Ch. 3.3 - In Exercises 20-23, solve the given matrix...Ch. 3.3 - In Exercises 20-23, solve the given matrix...Ch. 3.3 - In Exercises let
In each case, find an...Ch. 3.3 - Prob. 25EQCh. 3.3 - Prob. 26EQCh. 3.3 - Prob. 27EQCh. 3.3 - Prob. 28EQCh. 3.3 - Prob. 29EQCh. 3.3 - Prob. 30EQCh. 3.3 - Prob. 31EQCh. 3.3 - Prob. 32EQCh. 3.3 - In Exercises 31-38, find the inverse of the given...Ch. 3.3 - In Exercises 31-38, find the inverse of the given...Ch. 3.3 - In Exercises 31-38, find the inverse of the given...Ch. 3.3 - In Exercises 31-38, find the inverse of the given...Ch. 3.3 - Prob. 48EQCh. 3.3 - Prob. 49EQCh. 3.3 - In Exercises 48-63, use the Gauss-Jordan method to...Ch. 3.3 - Prob. 51EQCh. 3.3 - In Exercises 48-63, use the Gauss-Jordan method to...Ch. 3.3 - In Exercises 48-63, use the Gauss-Jordan method to...Ch. 3.3 - Prob. 54EQCh. 3.3 - Prob. 55EQCh. 3.3 - In Exercises 48-63, use the Gauss-Jordan method to...Ch. 3.3 - In Exercises 48-63, use the Gauss-Jordan method to...Ch. 3.3 - Prob. 60EQCh. 3.3 - Prob. 61EQCh. 3.3 - In Exercises 48-63, use the Gauss-Jordan method to...Ch. 3.3 - In Exercises 48-63, use the Gauss-Jordan method to...Ch. 3.4 - In Exercises 1 -6, solve the system Ax = b using...Ch. 3.4 - In Exercises 1 6, solve the system Ax = b using...Ch. 3.4 - In Exercises 1 -6, solve the system Ax = b using...Ch. 3.4 - In Exercises 1 -6, solve the system Ax = b using...Ch. 3.4 - In Exercises 1-6, solve the system Ax = b using...Ch. 3.4 - Prob. 6EQCh. 3.4 - In Exercises 7-12, find an LU factorization of the...Ch. 3.4 - In Exercises 7-12,find an LU factorization of the...Ch. 3.4 - In Exercises 7-12, find an LU factorization of the...Ch. 3.4 - In Exercises 7-12,find an LU factorization of the...Ch. 3.4 - In Exercises 7-12,find an LU factorization of the...Ch. 3.4 - Prob. 12EQCh. 3.4 - Generalize the definition of LU factorization to...Ch. 3.4 - Prob. 14EQCh. 3.5 - In Exercises 1-4, let S be the collection of...Ch. 3.5 - In Exercises 5-8, let S be the collection of...Ch. 3.5 - In Exercises 11 and 12, determine whether b is in...Ch. 3.5 - If A is the matrix in Exercise 12, is v=[712] in...Ch. 3.6 - 1. Let Ta : ℝ2 → ℝ2 be the matrix transformation...Ch. 3.6 - Let TA: 23 be the matrix transformation...Ch. 3.6 - In Exercises 3-6, prove that the given...Ch. 3.6 - In Exercises 3-6, prove that the given...Ch. 3.6 - Prob. 5EQCh. 3.6 - In Exercises 3-6, prove that the given...Ch. 3.6 - In Exercises 7-10, give a counterexample to show...Ch. 3.6 - In Exercises 7-10, give a counterexample to show...Ch. 3.6 - In Exercises 7-10, give a counterexample to show...Ch. 3.6 - In Exercises 7-10, give a counterexample to show...Ch. 3.6 - In Exercises 11-14, find the standard matrix of...Ch. 3.6 - In Exercises 11-14, find the standard matrix of...Ch. 3.6 - In Exercises 11-14, find the standard matrix of...Ch. 3.6 - In Exercises 11-14, find the standard matrix of...Ch. 3.6 - In Exercises 15-18, show that the given...Ch. 3.6 - In Exercises 15-18, show that the given...Ch. 3.6 - Prob. 17EQCh. 3.6 - Prob. 18EQCh. 3.6 - In Exercises 20-25, find the standard matrix of...Ch. 3.6 - In Exercises 20-25, find the standard matrix of...Ch. 3.6 - In Exercises 20-25, find the standard matrix of...Ch. 3.6 - In Exercises 20-25, find the standard matrix of...Ch. 3.6 - In Exercises 20-25, find the standard matrix of...Ch. 3.6 - In Exercises 20-25, find the standard matrix of...Ch. 3.6 - In Exercises30-35, verify Theorem 3.32 by finding...Ch. 3.6 - In Exercises 30-35, verify Theorem 3.32 by finding...Ch. 3.6 - In Exercises 30-35, verify Theorem 3.32 by finding...Ch. 3.6 - In Exercises 30-35, verify Theorem 3.32 by finding...Ch. 3.6 - In Exercises30-35, verify Theorem 3.32 by finding...Ch. 3.6 - Prob. 35EQCh. 3.7 - In Exercises 1-4, let be the transition matrix...Ch. 3.7 - Prob. 2EQCh. 3.7 - In Exercises 1-4, let P=[0.50.30.50.7] be the...Ch. 3.7 - In Exercises 1-4, let be the transition matrix for...Ch. 3.7 - Prob. 5EQCh. 3.7 - Prob. 6EQCh. 3.7 - Prob. 7EQCh. 3.7 - Prob. 8EQCh. 3.7 -
12. Robots have been programmed to traverse the...Ch. 3.7 - Prob. 31EQCh. 3.7 - Prob. 32EQCh. 3.7 - Prob. 33EQCh. 3.7 - Prob. 34EQCh. 3.7 - Prob. 35EQCh. 3.7 - Prob. 36EQCh. 3.7 - Prob. 37EQCh. 3.7 - Prob. 38EQCh. 3.7 - Prob. 39EQCh. 3.7 - Prob. 40EQCh. 3.7 - In Exercises 45-48, determine the adjacency matrix...Ch. 3.7 - Prob. 46EQCh. 3.7 - In Exercises 45-48, determine the adjacency matrix...Ch. 3.7 - In Exercises 45-48, determine the adjacency matrix...Ch. 3.7 - Prob. 53EQCh. 3.7 - In Exercises 53-56, determine the adjacency matrix...Ch. 3.7 - In Exercises 53-56, determine the adjacency matrix...Ch. 3.7 - In Exercises 53-56, determine the adjacency matrix...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Solve questions by Course Name (Ordinary Differential Equations II 2)arrow_forwardplease Solve questions by Course Name( Ordinary Differential Equations II 2)arrow_forwardInThe Northern Lights are bright flashes of colored light between 50 and 200 miles above Earth. Suppose a flash occurs 150 miles above Earth. What is the measure of arc BD, the portion of Earth from which the flash is visible? (Earth’s radius is approximately 4000 miles.)arrow_forward
- e). n! (n - 1)!arrow_forwardSuppose you flip a fair two-sided coin four times and record the result. a). List the sample space of this experiment. That is, list all possible outcomes that could occur when flipping a fair two-sided coin four total times. Assume the two sides of the coin are Heads (H) and Tails (T).arrow_forwarde). n! (n - 1)!arrow_forward
- Evaluate the following expression and show your work to support your calculations. a). 6! b). 4! 3!0! 7! c). 5!2! d). 5!2! e). n! (n - 1)!arrow_forwardAmy and Samiha have a hat that contains two playing cards, one ace and one king. They are playing a game where they randomly pick a card out of the hat four times, with replacement. Amy thinks that the probability of getting exactly two aces in four picks is equal to the probability of not getting exactly two aces in four picks. Samiha disagrees. She thinks that the probability of not getting exactly two aces is greater. The sample space of possible outcomes is listed below. A represents an ace, and K represents a king. Who is correct?arrow_forwardConsider the exponential function f(x) = 12x. Complete the sentences about the key features of the graph. The domain is all real numbers. The range is y> 0. The equation of the asymptote is y = 0 The y-intercept is 1arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY