
Concept explainers
(a)
The value of
(a)
Answer to Problem 50P
The value of
Explanation of Solution
Write the expression for the relation between the object distance, image distance and focal length.
Here,
Write the expression for magnification.
Here,
Write the expression for the relation between height and magnification.
Here,
Substitute
Conclusion:
Substitute
Substitute
Substitute
Substitute
Therefore, the value of
(b)
The sketch of the image.
(b)
Answer to Problem 50P
The sketch of the image is given in figure 1.
Explanation of Solution
The following figure gives the diagrammatic representation of the image formed by the thin lens.
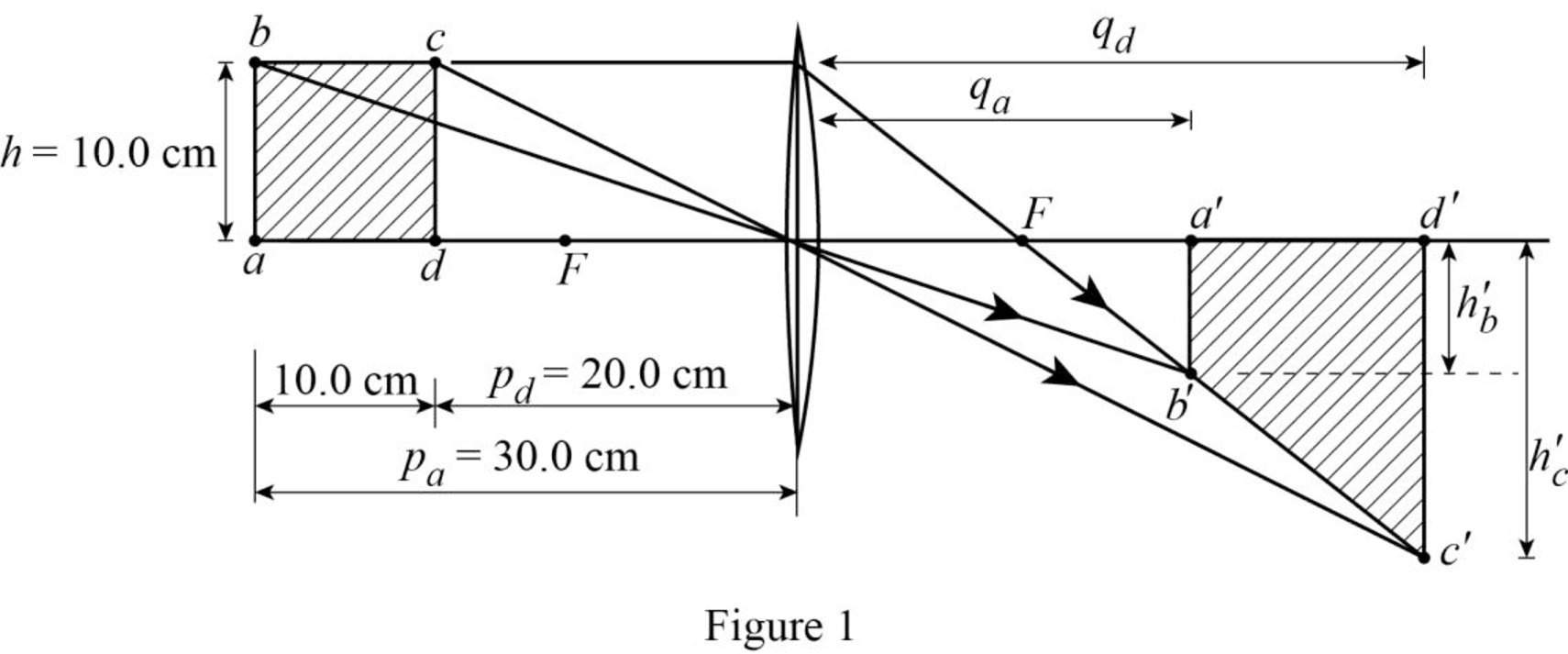
Conclusion:
Therefore, the sketch of the image is given in figure 1.
(c)
To demonstrate that the area is
(c)
Answer to Problem 50P
It is demonstrated that the area is
Explanation of Solution
Substitute
Conclusion:
Substitute
Write the expression for the modulus of the above equation.
Therefore, it is demonstrated that the area is
(d)
The reason for the area to be
(d)
Answer to Problem 50P
The integral will add up the area of the whole image.
Explanation of Solution
The vertical dimension of the image is given by
Therefore, the integral will add up the area of the whole image.
(e)
The area of the image.
(e)
Answer to Problem 50P
The area of the image is
Explanation of Solution
Write the expression for the area of the image.
Conclusion:
Substitute
Therefore, the area of the image is
Want to see more full solutions like this?
Chapter 36 Solutions
Physics for Scientists and Engineers with Modern Physics, Technology Update
- Pls help asaparrow_forward3. If the force of gravity stopped acting on the planets in our solar system, what would happen? a) They would spiral slowly towards the sun. b) They would continue in straight lines tangent to their orbits. c) They would continue to orbit the sun. d) They would fly straight away from the sun. e) They would spiral slowly away from the sun. 4. 1 The free-body diagram of a wagon being pulled along a horizontal surface is best represented by A F N B C 0 Ꭰ FN E a) A b) B c) C app app The app 10 app d) e) ס ח D E 10 apparrow_forwardPls help ASAParrow_forward
- Pls help asaparrow_forwardPls help asaparrow_forwardThe acceleration of an object sliding along a frictionless ramp is inclined at an angle 0 is 9. a) g tano b) g cose c) g sino 10. d) g e) zero A 1.5 kg cart is pulled with a force of 7.3 N at an angle of 40° above the horizontal. If a kinetic friction force of 3.2 N acts against the motion, the cart's acceleration along the horizontal surface will be a) 5.0 m/s² b) 1.6 m/s² c) 2.4 m/s² 11. d) 1.0 m/s² e) 2.7 m/s² What is the net force acting on an object with a mass of 10 kg moving at a constant velocity of 10 m/s [North]? a) 100 N [North] b) 100 N [South] 10 N [North} d) 10 N [South] e) None of these.arrow_forward
- Modified True/False - indicate whether the sentence or statement is true or false. If the statement is false, correct the statement to make it true. 12. An object in uniform circular motion has a constant velocity while experiencing centripetal acceleration. 13. An object travelling in uniform circular motion experiences an outward centrifugal force that tends to pull the object out of the circular path. 14. An object with less inertia can resist changes in motion more than an object with more inertia. 15. For an object sliding on a horizontal surface with a horizontal applied force, the frictional force will always increase as the applied force increases.arrow_forwardPls help asaparrow_forwardAnswer the given question showing step by step by and all necessary working out.arrow_forward
 Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax





