Chapter 3.4, Problem 71E

(a.)

To determine

An equation for this tangent line.

Answer to Problem 71E

It has been determined that an equation for the given tangent line is $y=\frac{1}{e}x$ .

Explanation of Solution

Given:

The line through the origin tangent to the graph of $y=\ln x$ has slope $\frac{1}{e}$ .

Concept used:

The equation of a line passing through the origin and having slope $m$ is $y=mx$ .

Calculation:

It is given that the line through the origin tangent to the graph of $y=\ln x$ has slope $\frac{1}{e}$ .

Then, this tangent line passes through the origin and has slope $\frac{1}{e}$ .

So, $m=\frac{1}{e}$ .

Put $m=\frac{1}{e}$ in $y=mx$ to get,

  $y=\frac{1}{e}x$

This is the required equation.

Conclusion:

It has been determined that an equation for the given tangent line is $y=\frac{1}{e}x$ .

(b.)

To determine

An argument based on the graphs of $y=\ln x$ and the tangent line to explain why $\ln x<\frac{x}{e}$ for all positive $x\ne e$ .

Answer to Problem 71E

It has been explained why $\ln x<\frac{x}{e}$ for all positive $x\ne e$ .

Explanation of Solution

Given:

The line through the origin tangent to the graph of $y=\ln x$ has slope $\frac{1}{e}$ .

Concept used:

The equation of a line passing through the origin and having slope $m$ is $y=mx$ .

Calculation:

As determined previously, the equation of the tangent is $y=\frac{1}{e}x$ .

The graphs of $y=\ln x$ and $y=\frac{1}{e}x$ are given as follows:

  

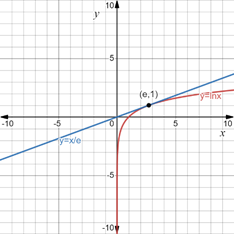
It can be seen that the graphs of $y=\ln x$ and $y=\frac{1}{e}x$ intersect when $x=e$ and other than this point, the graph of $y=\ln x$ always lies below the graph of $y=\frac{1}{e}x$ .

It should also be noted that the graph of $y=\ln x$ exists only for positive $x$ .

This implies that $\ln x<\frac{x}{e}$ for all positive $x\ne e$ .

This is the required proof.

Conclusion:

It has been explained why $\ln x<\frac{x}{e}$ for all positive $x\ne e$ .

(c.)

To determine

To Show: $\ln \left(x^e\right)<x$ for all positive $x\ne e$ .

Answer to Problem 71E

It has been shown that $\ln \left(x^e\right)<x$ for all positive $x\ne e$ .

Explanation of Solution

Given:

The line through the origin tangent to the graph of $y=\ln x$ has slope $\frac{1}{e}$ .

Concept used:

The equation of a line passing through the origin and having slope $m$ is $y=mx$ .

Calculation:

As shown previously, $\ln x<\frac{x}{e}$ for all positive $x\ne e$ .

Since $e>0$ , multiplying both sides of an inequality by $e$ does not change the inequality.

Now, $\ln x<\frac{x}{e}$ for all positive $x\ne e$ .

Multiplying both sides of the above inequality by $e$ ,

  $e\ln x<x$ for all positive $x\ne e$ .

Simplifying using property of logarithm,

  $\ln \left(x^e\right)<x$ for all positive $x\ne e$ .

This is the required proof.

Conclusion:

It has been shown that $\ln \left(x^e\right)<x$ for all positive $x\ne e$ .

(d.)

To determine

To Show: $x^e<e^x$ for all positive $x\ne e$ .

Answer to Problem 71E

It has been shown that $x^e<e^x$ for all positive $x\ne e$ .

Explanation of Solution

Given:

The line through the origin tangent to the graph of $y=\ln x$ has slope $\frac{1}{e}$ .

Concept used:

The equation of a line passing through the origin and having slope $m$ is $y=mx$ .

Calculation:

As shown previously, $\ln \left(x^e\right)<x$ for all positive $x\ne e$ .

Since the exponential function, $e^x$ is an increasing function, $a<b$ implies $e^a<e^b$ .

Now, $\ln \left(x^e\right)<x$ for all positive $x\ne e$ .

This implies that $e^{\ln \left(x^e\right)}<e^x$ for all positive $x\ne e$ .

Simplifying, $x^e<e^x$ for all positive $x\ne e$ .

This is the required proof.

Conclusion:

It has been shown that $x^e<e^x$ for all positive $x\ne e$ .

(e.)

To determine

Which is bigger; ${\pi }^e$ or $e^{\pi }$ .

Answer to Problem 71E

It has been determined that that $e^{\pi }$ is bigger than ${\pi }^e$ .

Explanation of Solution

Given:

The line through the origin tangent to the graph of $y=\ln x$ has slope $\frac{1}{e}$ .

Concept used:

The equation of a line passing through the origin and having slope $m$ is $y=mx$ .

Calculation:

As shown previously, $x^e<e^x$ for all positive $x\ne e$ .

Put $x=\pi$ in the above inequality to get,

  ${\pi }^e<e^{\pi }$

This implies that $e^{\pi }$ is bigger than ${\pi }^e$ .

Conclusion:

It has been determined that that $e^{\pi }$ is bigger than ${\pi }^e$ .