
(a)
To find: The graph of
(a)
Answer to Problem 69E
Graph is given.
Explanation of Solution
Given information:
Calculation:
The meaning of
Differentiate
To find the value of
Now given that
Draw the graph of
The graph will be the horizontal lines as
When
When
Similarly, for other values of
The graph for different values of
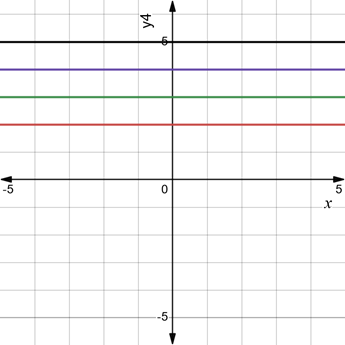
For equation
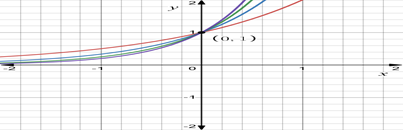
It can be seen that as the exponent increases, the curves get steeper and the rate of growth increases respectively. A function which grows faster than a polynomial function is
Thus, the exponential function having base greater than 1, i.e.,
It must be noted that the exponential function is increasing and the point
(b)
To find: The graph of
(b)
Answer to Problem 69E
The graph is given and values of
Explanation of Solution
Given information:
Calculation:
The meaning of
Differentiate
To find the value of
Draw the graph of
When
When
When
The graph of
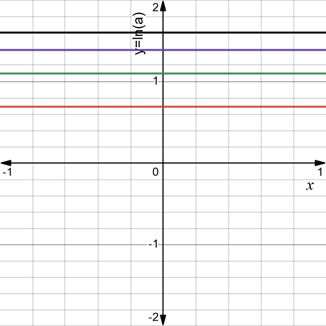
For
Therefore the values of
Basically the value found of
Here,
Table of values of
| 2 | 3 | 4 | 5 | |
| 0.69 | 1.098 | 1.386 | 1.60 |
(c)
To find: How part
(c)
Explanation of Solution
Given information:
Calculation:
The meaning of
Differentiate
To find the value of
In part (a) the value
If
Recall the fact that exponent and log functions are inverse to each other therefore
Hence
This proves that if
Hence proved.
(d)
To find: prove algebraically
(d)
Explanation of Solution
Given information:
Calculation:
The meaning of
Differentiate
If
Therefore it can be written as
Chapter 3 Solutions
Advanced Placement Calculus Graphical Numerical Algebraic Sixth Edition High School Binding Copyright 2020
- 3. We'd like to know the first time when the population reaches 7000 people. First, graph the function from part (a) on your calculator or Desmos. In the same window, graph the line y = 7000. Notice that you will need to adjust your window so that you can see values as big as 7000! Investigate the intersection of the two graphs. (This video shows you how to find the intersection on your calculator, or in Desmos just hover the cursor over the point.) At what value t> 0 does the line intersect with your exponential function? Round your answer to two decimal places. (You don't need to show work for this part.) (2 points)arrow_forwardSuppose the planet of Tattooine currently has a population of 6500 people and an annual growth rate of 0.35%. Use this information for all the problems below. 1. Find an exponential function f(t) that gives the population of Tattooine t years from now. (3 points)arrow_forwardA house was valued at $95,000 in the year 1988. The value appreciated to $170,000 by the year 2007. A) If the value is growing exponentially, what was the annual growth rate between 1988 and 2007? Round the growth rate to 4 decimal places. r = B) What is the correct answer to part A written in percentage form? r = 3 %.arrow_forward
- B G R + K Match each equation with a graph above - 3(0.9)* 1 a. green (G) 3(1.5)* b. black (K) 3(0.73)* c. blue (B) d. red (R) I ✪ 4(1.21)* - 3(1.21)* e. orange (O)arrow_forwardSuppose the planet of Tattooine currently has a population of 6500 people and an annual growth rate of 0.35%. Use this information for all the problems below.arrow_forwardTwo cables tied together at C are loaded as shown. Given: Q = 130 lb. 8 30° C B Q 3 4 Draw the free-body diagram needed to determine the range of values of P for which both cables remain taut.arrow_forward
- Cable AB is 103 ft long and the tension in the cable is 3900 lb. 56 ft A 50° 20° B x C Identify the angles 0.0, and 8, that define the direction of force. 1 By N 2 Match each of the options above to the items below. 142.1° 57.1° 73.3° 3 8.arrow_forwardIn the given figure, P = 51 lb . 65° C 25° 35° 75 lb P Determine the corresponding magnitude of the resultant. The corresponding magnitude of the resultant is| lb.arrow_forwardCable AB is 103 ft long and the tension in the cable is 3900 lb. 56 ft D y A B 20° 50° x C Identify the x, y, and z components of the force exerted by the cable on the anchor B. 1 F. FI 3 Fy 2 Match each of the options above to the items below. 2,120 lb 1,120 lb -3,076 lbarrow_forward
- In the given figure, P = 51 lb. 65° 25° 35° 75 lb P B Determine the required tension in cable AC, knowing that the resultant of the three forces exerted at point C of boom BC must be directed along BC. The required tension in cable AC is lb.arrow_forwardhelp on this question about Laplace transformation?arrow_forwardHelp me expand this fraction below.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





