
Use Theorem 3.9 or Algorithm 3.3 to construct an approximating polynomial for the following data.
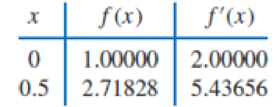
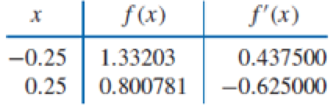

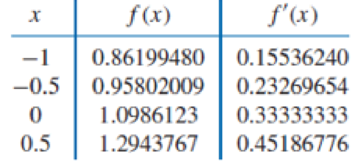
ALGORITHM 3.3
Hermite Interpolation
To obtain the coefficients of the Hermite interpolating polynomial H(x) on the (n + 1) distinct numbers x0, …, xn for the function f:
INPUT numbers x0, x1, …, xn; values f (x0), ... , f (xn) and f′ (x0), ... , f′ (xn).
OUTPUT the numbers Q0, 0, Q1, 1, … , Q2n + 1, 2n + 1 where
Step 1 For i = 0, 1, … , n do Steps 2 and 3.
Step 2
Step 3 If i ≠ 0 then set
Step 4 For i = 2, 3, … , 2n + 1
for j = 2, 3, ... , i set
Step 5 OUTPUT (Q0, 0, Q1, 1, … , Q2n + 1, 2n + 1);
STOP.
Theorem 3.9 If f ∈ C1 [a, b] and x0, …, xn ∈ [a, b] are distinct, the unique polynomial of least degree agreeing with f and f′ at x0, …, xn is the Hermite polynomial of degree at most 2n + 1 given by
where, for Ln, j (x) denoting the jth Lagrange coefficient polynomial of degree n, we have
Moreover, if f ∈ C2n + 2 [a, b], then
for some (generally unknown) ξ(x) in the interval (a, b).
Trending nowThis is a popular solution!

Chapter 3 Solutions
Numerical Analysis
Additional Math Textbook Solutions
Pathways To Math Literacy (looseleaf)
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Precalculus: A Unit Circle Approach (3rd Edition)
Precalculus
Elementary & Intermediate Algebra
- d((x, y), (z, w)) = |xz|+|yw|, show that whether d is a metric on R² or not?. Q3/Let R be a set of real number and d: R² x R² → R such that -> d((x, y), (z, w)) = max{\x - zl, ly - w} show that whether d is a metric on R² or not?. Q4/Let X be a nonempty set and d₁, d₂: XXR are metrics on X let d3,d4, d5: XX → R such that d3(x, y) = 4d2(x, y) d4(x, y) = 3d₁(x, y) +2d2(x, y) d5(x,y) = 2d₁ (x,y))/ 1+ 2d₂(x, y). Show that whether d3, d4 and d5 are metric on X or not?arrow_forwardplease Solve questions by Course Name( Ordinary Differential Equations II 2)arrow_forwardBusiness discussarrow_forward
- please do Q3arrow_forwardUse the properties of logarithms, given that In(2) = 0.6931 and In(3) = 1.0986, to approximate the logarithm. Use a calculator to confirm your approximations. (Round your answers to four decimal places.) (a) In(0.75) (b) In(24) (c) In(18) 1 (d) In ≈ 2 72arrow_forwardFind the indefinite integral. (Remember the constant of integration.) √tan(8x) tan(8x) sec²(8x) dxarrow_forward
- Find the indefinite integral by making a change of variables. (Remember the constant of integration.) √(x+4) 4)√6-x dxarrow_forwardInThe Northern Lights are bright flashes of colored light between 50 and 200 miles above Earth. Suppose a flash occurs 150 miles above Earth. What is the measure of arc BD, the portion of Earth from which the flash is visible? (Earth’s radius is approximately 4000 miles.)arrow_forwardJu at © Ju 370 = x (- пье zxp = c² (2² 4 ) dx² ахе 2 nze dyz t nzp Q/what type of partial differential equation (PDE) are the following-arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning  Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,
Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,



