Numerical Analysis
10th Edition
ISBN: 9781305253667
Author: Richard L. Burden, J. Douglas Faires, Annette M. Burden
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 3.3, Problem 12ES
The following data are given for a polynomial P(x) of unknown degree.
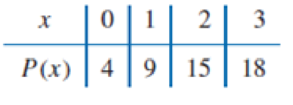
Determine the coefficient of x3 in P(x) if all fourth-order forward differences are 1.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Ju
at
© Ju
370
= x (-
пье
zxp
= c² (2² 4 )
dx²
ахе
2
nze
dyz
t
nzp
Q/what type of partial differential equation (PDE)
are the following-
Q
Calculate the Fourier series for
f(x) = x
on
the interval -16≤x≤ T
BUSINESS DISCUSS
Chapter 3 Solutions
Numerical Analysis
Ch. 3.1 - For the given functions f(x), let x0 = 0, x1 =...Ch. 3.1 - Use Theorem 3.3 to find an error bound for the...Ch. 3.1 - Prob. 4ESCh. 3.1 - The data for Exercise 6 were generated using the...Ch. 3.1 - Prob. 9ESCh. 3.1 - Prob. 10ESCh. 3.1 - Prob. 11ESCh. 3.1 - Prob. 12ESCh. 3.1 - Prob. 15ESCh. 3.1 - Prob. 17ES
Ch. 3.1 - It is suspected that the high amounts of tannin in...Ch. 3.1 - Prob. 21ESCh. 3.1 - Prove Taylors Theorem 1.14 by following the...Ch. 3.1 - Prob. 1DQCh. 3.1 - If we decide to increase the degree of the...Ch. 3.2 - Let P3(x) be the interpolating polynomial for the...Ch. 3.2 - Nevilles method is used to approximate f(0.4),...Ch. 3.2 - Nevilles method is used to approximate f(0.5),...Ch. 3.2 - Suppose xj = j, for j = 0, 1, 2, 3, and it is...Ch. 3.2 - Nevilles Algorithm is used to approximate f(0)...Ch. 3.2 - Prob. 11ESCh. 3.2 - Prob. 13ESCh. 3.2 - Can Nevilles method be used to obtain the...Ch. 3.3 - Use Eq. (3.10) or Algorithm 3.2 to construct...Ch. 3.3 - Use Eq. (3.10) or Algorithm 3.2 to construct...Ch. 3.3 - Use the Newton forward-difference formula to...Ch. 3.3 - Use the Newton forward-difference formula to...Ch. 3.3 - Use the Newton backward-difference formula to...Ch. 3.3 - Use the Newton backward-difference formula to...Ch. 3.3 - a. Use Algorithm 3.2 to construct the...Ch. 3.3 - a. Use Algorithm 3.2 to construct the...Ch. 3.3 - a. Approximate f(0.05) using the following data...Ch. 3.3 - The following data are given for a polynomial P(x)...Ch. 3.3 - The following data are given for a polynomial P(x)...Ch. 3.3 - The Newton forward-difference formula is used to...Ch. 3.3 - Prob. 14ESCh. 3.3 - Prob. 16ESCh. 3.3 - Prob. 17ESCh. 3.3 - Show that the polynomial interpolating the...Ch. 3.3 - Prob. 20ESCh. 3.3 - Prob. 21ESCh. 3.3 - Prob. 22ESCh. 3.3 - Prob. 23ESCh. 3.3 - Compare and contrast the various...Ch. 3.3 - Is it easier to add a new data pair using...Ch. 3.3 - Prob. 3DQCh. 3.4 - Use Theorem 3.9 or Algorithm 3.3 to construct an...Ch. 3.4 - Use Theorem 3.9 or Algorithm 3.3 to construct an...Ch. 3.4 - The data in Exercise 1 were generated using the...Ch. 3.4 - The data in Exercise 2 were generated using the...Ch. 3.4 - Let f (x) = 3xex e2x. a. Approximate f (1.03) by...Ch. 3.4 - The following table lists data for the function...Ch. 3.4 - a. Show that H2n + 1 (x) is the unique polynomial...Ch. 3.4 - Prob. 1DQCh. 3.4 - Prob. 2DQCh. 3.4 - Prob. 3DQCh. 3.5 - Determine the natural cubic spline S that...Ch. 3.5 - Determine the clamped cubic spline s that...Ch. 3.5 - Construct the natural cubic spline for the...Ch. 3.5 - Construct the natural cubic spline for the...Ch. 3.5 - The data in Exercise 3 were generated using the...Ch. 3.5 - Prob. 6ESCh. 3.5 - Prob. 8ESCh. 3.5 - Prob. 11ESCh. 3.5 - Prob. 12ESCh. 3.5 - Prob. 13ESCh. 3.5 - Prob. 14ESCh. 3.5 - Given the partition x0 = 0, x1 = 0.05, and x2 =...Ch. 3.5 - Prob. 16ESCh. 3.5 - Prob. 21ESCh. 3.5 - Prob. 22ESCh. 3.5 - Prob. 23ESCh. 3.5 - It is suspected that the high amounts of tannin in...Ch. 3.5 - Prob. 29ESCh. 3.5 - Prob. 30ESCh. 3.5 - Prob. 31ESCh. 3.5 - Prob. 32ESCh. 3.5 - Let f C2[a, b] and let the nodes a = x0 x1 xn...Ch. 3.5 - Prob. 34ESCh. 3.5 - Prob. 35ESCh. 3.6 - Let (x0, y0) = (0,0) and (x1, y1) = (5, 2) be the...Ch. 3.6 - Prob. 2ESCh. 3.6 - Prob. 5ESCh. 3.6 - Prob. 1DQ
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- a -> f(x) = f(x) = [x] show that whether f is continuous function or not(by using theorem) Muslim_mathsarrow_forwardUse Green's Theorem to evaluate F. dr, where F = (√+4y, 2x + √√) and C consists of the arc of the curve y = 4x - x² from (0,0) to (4,0) and the line segment from (4,0) to (0,0).arrow_forwardWhen a tennis player serves, he gets two chances to serve in bounds. If he fails to do so twice, he loses the point. If he attempts to serve an ace, he serves in bounds with probability 3/8.If he serves a lob, he serves in bounds with probability 7/8. If he serves an ace in bounds, he wins the point with probability 2/3. With an in-bounds lob, he wins the point with probability 1/3. If the cost is '+1' for each point lost and '-1' for each point won, the problem is to determine the optimal serving strategy to minimize the (long-run)expected average cost per point. (Hint: Let state 0 denote point over,two serves to go on next point; and let state 1 denote one serve left. (1). Formulate this problem as a Markov decision process by identifying the states and decisions and then finding the Cik. (2). Draw the corresponding state action diagram. (3). List all possible (stationary deterministic) policies. (4). For each policy, find the transition matrix and write an expression for the…arrow_forward
- During each time period, a potential customer arrives at a restaurant with probability 1/2. If there are already two people at the restaurant (including the one being served), the potential customer leaves the restaurant immediately and never returns. However, if there is one person or less, he enters the restaurant and becomes an actual customer. The manager has two types of service configurations available. At the beginning of each period, a decision must be made on which configuration to use. If she uses her "slow" configuration at a cost of $3 and any customers are present during the period, one customer will be served and leave with probability 3/5. If she uses her "fast" configuration at a cost of $9 and any customers are present during the period, one customer will be served and leave with probability 4/5. The probability of more than one customer arriving or more than one customer being served in a period is zero. A profit of $50 is earned when a customer is served. The manager…arrow_forwardEvery Saturday night a man plays poker at his home with the same group of friends. If he provides refreshments for the group (at an expected cost of $14) on any given Saturday night, the group will begin the following Saturday night in a good mood with probability 7/8 and in a bad mood with probability 1/8. However, if he fail to provide refreshments, the group will begin the following Saturday night in a good mood with probability 1/8 and in a bad mood with probability 7/8 regardless of their mood this Saturday. Furthermore, if the group begins the night in a bad mood and then he fails to provide refreshments, the group will gang up on him so that he incurs expected poker losses of $75. Under other circumstances he averages no gain or loss on his poker play. The man wishes to find the policy regarding when to provide refreshments that will minimize his (long-run) expected average cost per week. (1). Formulate this problem as a Markov decision process by identifying the states and…arrow_forwardThis year Amanda decides to invest in two different no-load mutual funds: the G Fund or the L Mutual Fund. At the end of each year, she liquidates her holdings, takes her profits, and then reinvests. The yearly profits of the mutual funds depend on where the market stood at the end of the preceding year. Recently the market has been oscillating around level 2 from one year end to the next, according to the probabilities given in the following transition matrix : L1 L2 L3 L1 0.2 0.4 0.4 L2 0.1 0.4 0.5 L3 0.3 0.3 0.4 Each year that the market moves up (down) 1 level, the G Fund has profits (losses) of $20k, while the L Fund has profits (losses) of $10k. If the market moves up (down) 2 level in a year, the G Fund has profits (losses) of $50k, while the L Fund has profits (losses) of only $20k. If the market does not change, there is no profit or loss for either fund. Amanda wishes to determine her optimal investment policy in order to maximize her (long-run) expected average profit per…arrow_forward
- A researcher wishes to estimate, with 90% confidence, the population proportion of adults who support labeling legislation for genetically modified organisms (GMOs). Her estimate must be accurate within 4% of the true proportion. (a) No preliminary estimate is available. Find the minimum sample size needed. (b) Find the minimum sample size needed, using a prior study that found that 65% of the respondents said they support labeling legislation for GMOs. (c) Compare the results from parts (a) and (b). ... (a) What is the minimum sample size needed assuming that no prior information is available? n = (Round up to the nearest whole number as needed.)arrow_forwardThe table available below shows the costs per mile (in cents) for a sample of automobiles. At a = 0.05, can you conclude that at least one mean cost per mile is different from the others? Click on the icon to view the data table. Let Hss, HMS, HLS, Hsuv and Hмy represent the mean costs per mile for small sedans, medium sedans, large sedans, SUV 4WDs, and minivans respectively. What are the hypotheses for this test? OA. Ho: Not all the means are equal. Ha Hss HMS HLS HSUV HMV B. Ho Hss HMS HLS HSUV = μMV Ha: Hss *HMS *HLS*HSUV * HMV C. Ho Hss HMS HLS HSUV =μMV = = H: Not all the means are equal. D. Ho Hss HMS HLS HSUV HMV Ha Hss HMS HLS =HSUV = HMVarrow_forwardQuestion: A company launches two different marketing campaigns to promote the same product in two different regions. After one month, the company collects the sales data (in units sold) from both regions to compare the effectiveness of the campaigns. The company wants to determine whether there is a significant difference in the mean sales between the two regions. Perform a two sample T-test You can provide your answer by inserting a text box and the answer must include: Null hypothesis, Alternative hypothesis, Show answer (output table/summary table), and Conclusion based on the P value. (2 points = 0.5 x 4 Answers) Each of these is worth 0.5 points. However, showing the calculation is must. If calculation is missing, the whole answer won't get any credit.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Finding Local Maxima and Minima by Differentiation; Author: Professor Dave Explains;https://www.youtube.com/watch?v=pvLj1s7SOtk;License: Standard YouTube License, CC-BY