
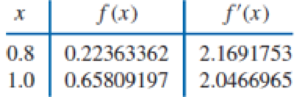
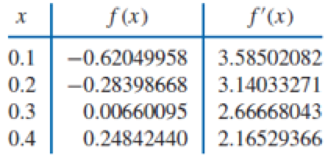
Use Theorem 3.9 or Algorithm 3.3 to construct an approximating polynomial for the following data.
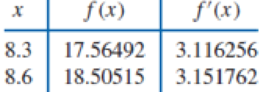

ALGORITHM 3.3
Hermite Interpolation
To obtain the coefficients of the Hermite interpolating polynomial H(x) on the (n + 1) distinct numbers x0, …, xn for the function f:
INPUT numbers x0, x1, …, xn; values f (x0), ... , f (xn) and f′ (x0), ... , f′ (xn).
OUTPUT the numbers Q0, 0, Q1, 1, … , Q2n + 1, 2n + 1 where
Step 1 For i = 0, 1, … , n do Steps 2 and 3.
Step 2
Step 3 If i ≠ 0 then set
Step 4 For i = 2, 3, … , 2n + 1
for j = 2, 3, ... , i set
Step 5 OUTPUT (Q0, 0, Q1, 1, … , Q2n + 1, 2n + 1);
STOP.
Theorem 3.9 If f ∈ C1 [a, b] and x0, …, xn ∈ [a, b] are distinct, the unique polynomial of least degree agreeing with f and f′ at x0, …, xn is the Hermite polynomial of degree at most 2n + 1 given by
where, for Ln, j (x) denoting the jth Lagrange coefficient polynomial of degree n, we have
Moreover, if f ∈ C2n + 2 [a, b], then
for some (generally unknown) ξ(x) in the interval (a, b).
Want to see the full answer?
Check out a sample textbook solution
Chapter 3 Solutions
Numerical Analysis
- What is the area of this figure? 3 mi 5 mi 6 mi 4 mi 2 mi 3 mi 6 mi Write your answer using decimals, if necessary. 5 miarrow_forwardμ=1 r = 30 mm 500 mm a 7000 mm b 7000 mm C 500 mmarrow_forwardPhil has systematically contributed $3000 to his RRSP at the beginning of every three months for the past 17 years.If the RRSP has earned 8.8% compounded quarterly, what is the value of Phil’s RRSP today? (Do not round intermediate calculations and round your final answer to 2 decimal places.)The value of the RRSP today $arrow_forward
- Answer all questions and show workarrow_forwardThe U.S. Bureau of Labor Statistics reports that 11.3% of U.S. workers belong to unions (BLS website, January 2014). Suppose a sample of 400 U.S. workers is collected in 2014 to determine whether union efforts to organize have increased union membership. a. Formulate the hypotheses that can be used to determine whether union membership increased in 2014.H 0: p H a: p b. If the sample results show that 52 of the workers belonged to unions, what is the p-value for your hypothesis test (to 4 decimals)?arrow_forwardFind a unit normal vector to the surface f(x, y, z) = 0 at the point P(-3,4, -32) for the function f(x, y, z) = In -4x -5y- Please write your answer as a vector (a, b, c) with a negative z component, and show your answer accurate to 4 decimal placesarrow_forward
- Answer this pleasearrow_forwardB1 The x distribution is a special case of Gamma distribution (not to be confused with gamma function; see below). The density function of the Gamma distribution with parameters and k is given by where -1 e -x/0 (x) = = г(k) Øk if x > 0, and otherwise, г(k) = √ ₁ k-1-x dx x' e is the gamma function. (a) For every k ≥ 1, 0 > 0, find the mode of the density. Hint: The algebra can be simplified by appropriate use of logarithms. ~ Now suppose that X1,..., Xn id Exp(\) and that we have a prior belief in A which is consistent with a prior distribution X. Gamma(a, b), for some a, ß, i.e. the prior density of is Baxa-1-BA T(a) e = so 01/ẞ and k = a. (b) Write down the likelihood, and show that the posterior distribution for \ is also a Gamma distribution, but with parameters a +n and B + Σ Xi. (c) Find the mode of the posterior distribution and examine the behaviour as n → ∞.arrow_forwardFind the differential of the function f(x, y) = 2x² - 2xy – 5y² at the point (-6, -5) using Ax = 0.3 and Ay = 0.05. dz = Now find Az and compare it to your answer above Ax= Hint: If entering a decimal, round to at least 5 placesarrow_forward
- Find the differential of the function f(x, y) = −8x√y at the point (1,3) using Ax = 0.25 and Ay = -0.15. dz Now find Az and compare it to your answer above Az = Hint: If entering a decimal, round to at least 5 placesarrow_forwardplease dont use chat gpt i need to underarrow_forwardChris Lynch plans to invest $200 into a money market account. Find the interest rate that is needed for the money to grow to $1,800 in 12 years if the interest is compounded quarterly. The rate is %. (Round to the nearest percent.)arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning  Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,
Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,



