Chapter 3.4, Problem 16E

Interpretation Introduction

Interpretation:

We are asked to plot the potentials of the non-linear differential equations of three different kinds of bifurcations.

a) Saddle node bifurcation

b) Transcritical bifurcation

c) Subcritical pitchfork bifurcation.

Concept Introduction:

Bifurcations and Bifurcation points - The qualitative structure of the flow can change as parameters are varied. In particular, fixed points can be created or destroyed, or their stability canchange. These qualitative changes in the dynamics are calledbifurcations, and the parameter values at which they occur are called bifurcation points.

Saddle node bifurcation is a mechanism by which the fixed points move toward each other and eventually annihilate.

Pitchfork bifurcation is the bifurcation mainly seen in symmetrical physical problems. Stable or unstable fixed points appear and disappear in pairs in such cases.

Problems in which pair of stable symmetric fixed points emerge are called subcritical pitchfork bifurcation.

Problems in which pair of unstable symmetric fixed points emerge are called supercritical pitchfork bifurcation.

In some physical systems, there exists a stable point irrespective of parameter values. (Either r < 0, r = 0 or r > 0) such cases are called transcritical bifurcation.

Answer to Problem 16E

Solution:

Plots for potentials of equations a, b and c with their different r values are plotted below.

Explanation of Solution

(a) We have,

${\dot{\text{x}}\text{ = r - x}}^{\text{2}}$

To find the potential $\text{V(x)}$

$\frac{\text{-dV}}{\text{dx}}{\text{= r - x}}^{\text{2}}$

${\text{dV= (- r + x}}^{\text{2}}\text{)dx}$

By integrating the above equation,

${\displaystyle \int \text{dV}=}{\displaystyle \int {\text{(- r + x}}^{\text{2}}\text{)dx}}$

$\text{V= -rx +}\frac{{\text{x}}^{\text{3}}}{\text{3}}+C$

Let’s take, $\text{C = 0}$ for convenience

$\text{V= -rx +}\frac{{\text{x}}^{\text{3}}}{\text{3}}$

To find the critical points, substitute $\text{0}$ for $\frac{\text{dV}}{\text{dx}}$,

${\text{r - x}}^{\text{2}}=0$

$\begin{array}{l}{\text{x}}^{\text{2}}\text{= r}\\ \text{x*= ±}\sqrt{\text{r}}\end{array}$

These are the fixed point of the potential function.

If r > 0, there are two fixed points, one stable and another unstable as the value of r decreases further, both points approach towards each other. At r = 0, both fixed points collide and annihilate after r <0 thus r = 0 issaddle-node bifurcationpoint.

Potential V(x) for different values of r is plotted below.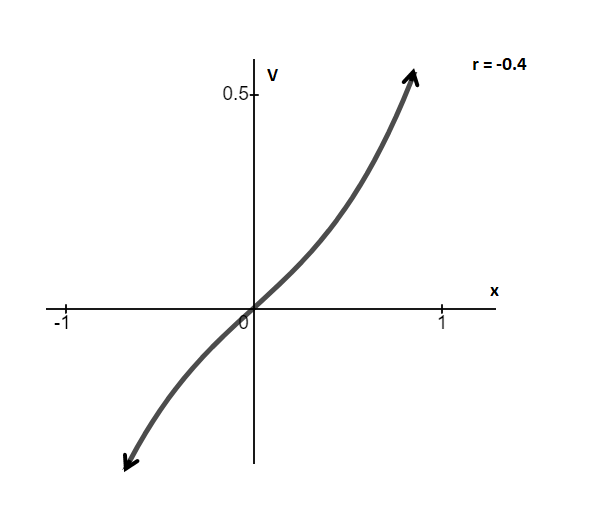

V vs. x for r = 0

V vs. x for r > 0

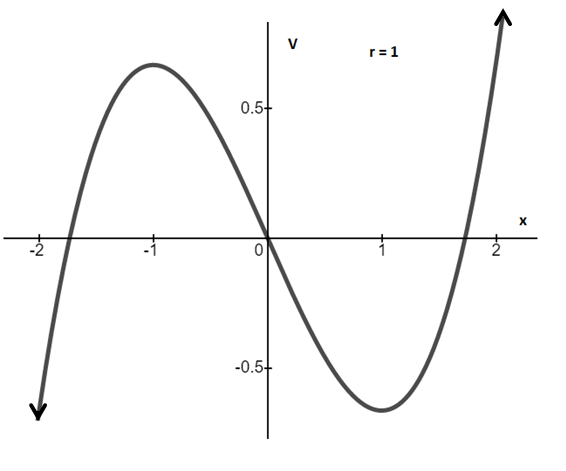
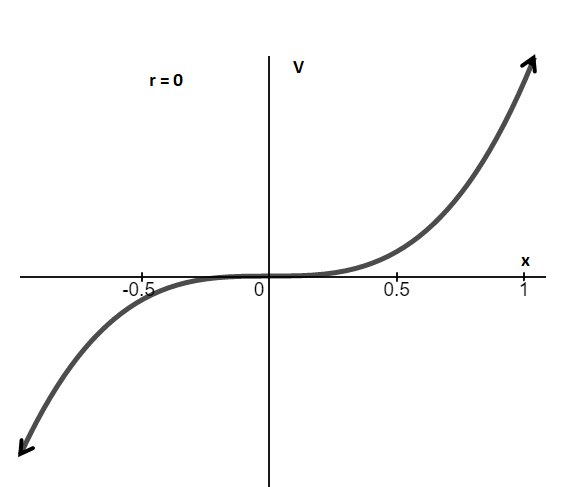
(b) The first-order system equation is

$\stackrel{\text{.}}{\text{x}}{\text{=rx-x}}^{\text{2}}$

To calculate the potential V(x) for the system let us use,

$\text{-}\frac{\text{dV}}{\text{dx}}{\text{=rx-x}}^{\text{2}}$

$\text{dv=}\left({\text{-rx+x}}^{\text{2}}\right)\text{dx}$

Integrating,

${\displaystyle \int \text{dv=}{\displaystyle \int \left({\text{-rx+x}}^{\text{2}}\right)\text{dx}}}$

$\text{v=-r}\frac{{\text{x}}^{\text{2}}}{\text{2}}\text{+}\frac{{\text{x}}^{\text{3}}}{\text{3}}$

To find the critical points, substitute 0 for $\frac{\text{dv}}{\text{dx}}$

${\text{rx-x}}^{\text{2}}\text{=0}$

$\text{x}\left(\text{r-x}\right)\text{=0}$

$\stackrel{\text{.}}{\text{x}}\text{= 0 and }\stackrel{\text{.}}{\text{x}}\text{ = r}$

As we can see, out of two fixed points, one point always lies on the origin and as parameter changes its value, fixed points change their stability.

Therefore, at r = 0, transcritical bifurcation occurs.

Potentials for different r valued are plotted below.

Graph between V and x for r < 0 (r = -1)

Graph between V and x for r = 0

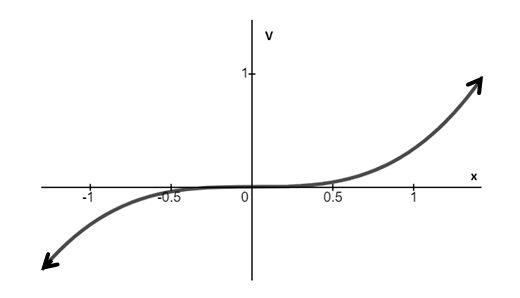
The graph between V and x for r>0

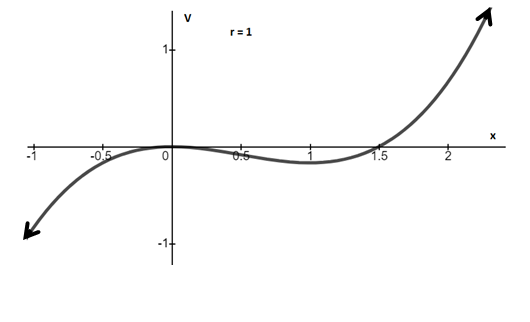
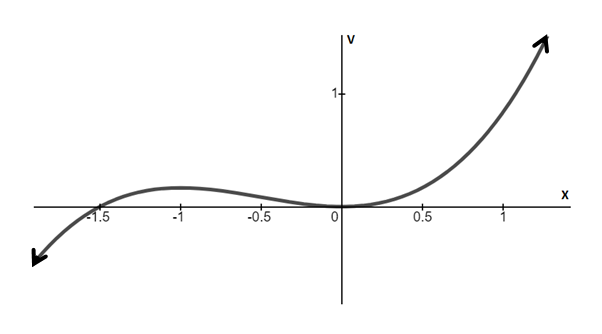
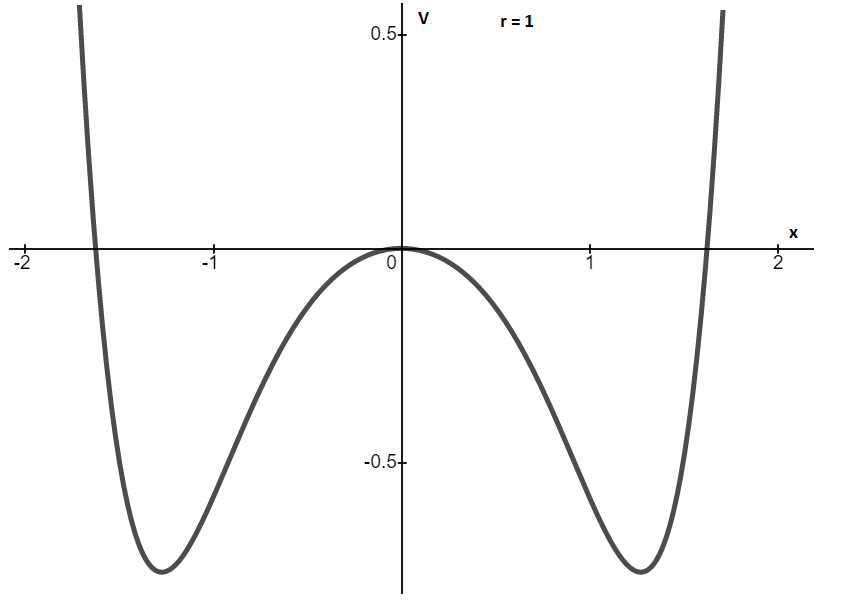
(c)

We have the equation of the system,

${\dot{\text{x}}\text{ = rx + x}}^{\text{3}}{\text{ - x}}^{\text{5}}$

To calculate the potential $\text{V(x)}$ for the system as:

$\begin{array}{l}\text{-}\frac{\text{dV}}{\text{dx}}{\text{ = rx + x}}^{\text{3}}{\text{ - x}}^{\text{5}}\\ {\text{dV = (- rx - x}}^{\text{3}}{\text{ + x}}^{\text{5}}\text{)dx}\end{array}$

Integrating,

$\begin{array}{l}{\displaystyle \int \text{dV = }{\displaystyle \int {\text{(- rx - x}}^{\text{3}}{\text{ + x}}^{\text{5}}\text{)}}}\\ \text{V = }\frac{\text{- rx}}{\text{2}}\text{ - }\frac{{\text{x}}^{\text{4}}}{\text{4}}\text{ + }\frac{{\text{x}}^{\text{6}}}{\text{6}}\text{ + C}\end{array}$

To find the critical points, substitute $\text{0}$ for $\frac{\text{dV}}{\text{dx}}$,

$\begin{array}{l}{\text{rx + x}}^{\text{3}}{\text{ - x}}^{\text{5}}\text{ = 0}\\ {\text{x(r + x}}^{\text{2}}{\text{ - x}}^{\text{4}}\text{) = 0}\end{array}$

${\text{x}}_{\text{1}}\text{ = 0}$

And

${\text{x}}^{\text{2}}\text{ = }\frac{\text{-1 ± }\sqrt{\text{1 + 4r}}}{\text{2}}$

Others fixed points are:

${\text{x}}_{\text{2}}\text{ = }\sqrt{\frac{\text{1 + }\sqrt{\text{1 + 4r}}}{\text{2}}}$

${\text{x}}_{\text{3}}\text{ = }\sqrt{\frac{\text{1 - }\sqrt{\text{1 + 4r}}}{\text{2}}}$

${\text{x}}_{\text{4}}\text{ = - }\sqrt{\frac{\text{1 + }\sqrt{\text{1 + 4r}}}{\text{2}}}$

${\text{x}}_{\text{5}}\text{ = - }\sqrt{\frac{\text{1 - }\sqrt{\text{1 + 4r}}}{\text{2}}}$

Obtain the second differentiation of the potential function,

$\frac{{\text{d}}^{\text{2}}\text{v}}{{\text{dx}}^{\text{2}}}{\text{ = - r + 3x}}^{\text{2}}{\text{ - 5x}}^{\text{4}}$

Local minima occur when,

$\frac{{\text{d}}^{\text{2}}\text{v}}{{\text{dx}}^{\text{2}}}\text{ > 0}$

Check out at differential points for the local minima as,

$\frac{{\text{d}}^{\text{2}}\text{v}}{{\text{dx}}^{\text{2}}}\text{ = - r > 0 if r < 0}$

${\left(\frac{{\text{d}}^{\text{2}}\text{v}}{{\text{dx}}^{\text{2}}}\right)}_{{\text{x}}_{\text{2}}}\text{= }{\left(\frac{{\text{d}}^{\text{2}}\text{v}}{{\text{dx}}^{\text{2}}}\right)}_{{\text{x}}_{\text{4}}}$

$$ $\text{= 4r + }\sqrt{\text{4r + 1}}\text{ + 1 > 0 if r > }\frac{\text{-1}}{\text{4}}$

Similarly,

${\left(\frac{{\text{d}}^{\text{2}}\text{v}}{{\text{dx}}^{\text{2}}}\right)}_{{\text{x}}_{\text{3}}}\text{= }{\left(\frac{{\text{d}}^{\text{2}}\text{v}}{{\text{dx}}^{\text{2}}}\right)}_{{\text{x}}_{\text{5}}}$

$\text{= 4r - }\sqrt{\text{4r + 1}}\text{ + 1 > 0 if r > 0}$

Therefore, three critical points wells occur at ${\text{x}}_{\text{1}}{\text{, x}}_{\text{2}}{\text{ and x}}_{\text{4}}\text{ with }\frac{\text{-1}}{\text{4}}\text{ < r < 0}\text{.}$

${\text{V(x}}_{\text{0}}\text{) = C}$

For simplicity, take $\text{C = 0}$, which gives,

$\begin{array}{l}{\text{V(x}}_{\text{2}}{\text{) = V(x}}_{\text{4}}\text{)}\\ {\text{ = V(x}}_{\text{0}}\text{)}\\ \end{array}$

Substitute $\sqrt{\frac{\text{1 + }\sqrt{\text{1 + 4r}}}{\text{2}}}$ for ${\text{x}}_{\text{2}}\text{ and 0 for C}$ in the potential equation.

$\frac{\text{1}}{\text{24}}\left({\text{- (4r + 1)}}^{\frac{\text{3}}{\text{2}}}\text{ - 6r - 1}\right)\text{ = 0}$

Further, solve for r,

$\begin{array}{l}\text{r = }\frac{\text{- 3}}{\text{16}}\\ {\text{ = r}}_{\text{c}}\end{array}$

Here, $r_c$ is the value of $\text{V}$ at the three local minima are equal.

Hence, ${\text{r}}_{\text{c}}\text{ = }\frac{\text{-3}}{\text{16}}$ and three minima ${\text{x}}_{\text{1}}{\text{, x}}_{\text{2}}{\text{ and x}}_{\text{4}}$ occur at the value of the integrating $\text{C}$.

Graphs of potential vs. position x are plotted below.

Graph between V and x for r<0

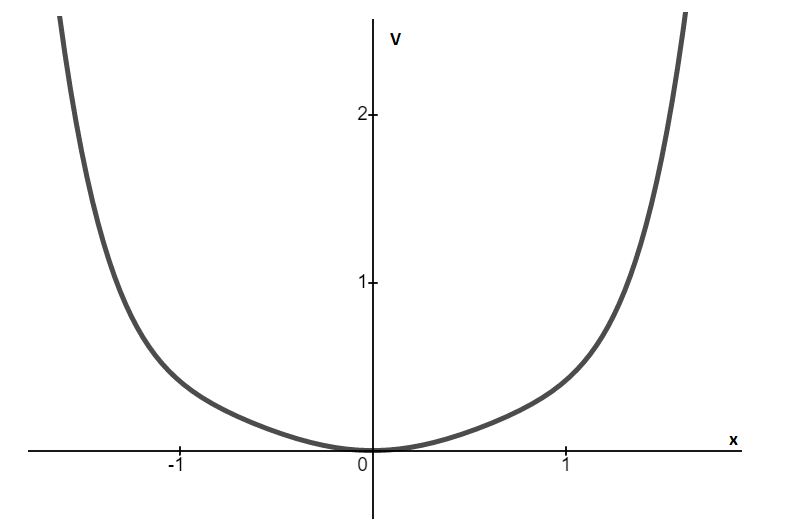
Graph between V and x for r=0

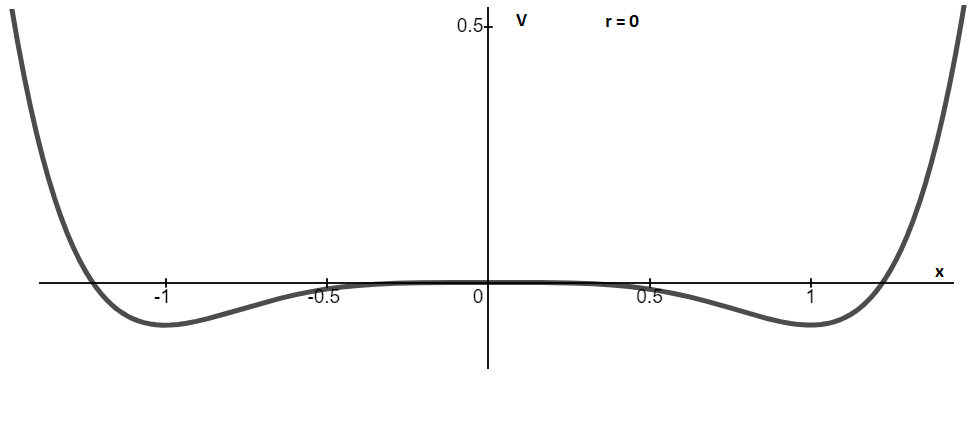
Graph between V and x for r>0