Chapter 33, Problem 72AP

(a)

To determine

The current in the circuit as a function of time.

Answer to Problem 72AP

The current in the circuit as a function of time is $\frac{\Delta V_{\max }\sin \omega t}{R}$.

Explanation of Solution

The circuit in which capacitor and inductor are short circuited and both the switch are closed is as shown below.

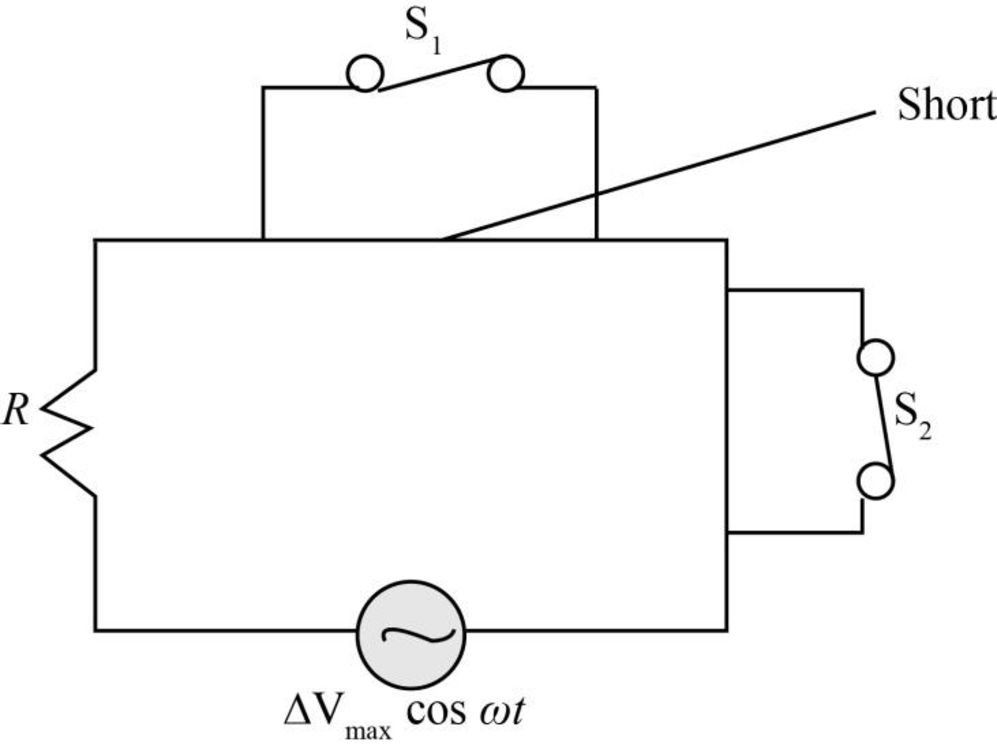
Figure-(1)

Write the expression to obtain the time varying voltage source.

    $\Delta v(t)=\Delta V_{\max }\cos \omega t$

Here, $\Delta v(t)$ is the time varying voltage source, $\Delta V_{\max }$ is the maximum voltage, $\omega$ is the angular frequency and $t$ is the time interval.

Write the expression to obtain the current in the circuit as a function of time.

    $i\left(t\right)=\frac{\Delta v\left(t\right)}{R}$

Here, $i\left(t\right)$ is the current in the circuit as a function of time, $\Delta v\left(t\right)$ is the time varying voltage source and $R$ is the resistance in the circuit.

Substitute $\Delta V_{\max }\cos \omega t$ for $\Delta v\left(t\right)$ in the above equation.

    $i\left(t\right)=\frac{\Delta V_{\max }\cos \omega t}{R}$

Conclusion:

Therefore, the current in the circuit as a function of time is $\frac{\Delta V_{\max }\cos \omega t}{R}$.

(b)

To determine

The power delivered to the circuit.

Answer to Problem 72AP

The power delivered to the circuit is $\frac{1}{2}\frac{\Delta V_{\max }^2}{R}$.

Explanation of Solution

Write the expression to obtain the power delivered to the circuit.

    $P=\frac{1}{2}\Delta V_{\max }{I}_{\max }$

Here, $P$ is the power delivered to the circuit, $\Delta V_{\max }$ is the maximum voltage across the circuit and $I_{\max }$ is the maximum current across the circuit.

Substitute $\frac{\Delta V_{\max }}{R}$ for $I_{\max }$ in the above equation.

    $\begin{array}{c}P=\frac{1}{2}\Delta V_{\max }\left(\frac{\Delta V_{\max }}{R}\right)\\ =\frac{1}{2}\frac{\Delta V_{\max }^2}{R}\end{array}$

Conclusion:

Therefore, the power delivered to the circuit is $\frac{1}{2}\frac{\Delta V_{\max }^2}{R}$.

(c)

To determine

The current in the circuit as function of time if only switch $1$ is open.

Answer to Problem 72AP

The current in the circuit as function of time if only switch $1$ is open is

Explanation of Solution

The circuit in which switch $1$ is open and capacitor act as a short circuited is as shown in the figure below.

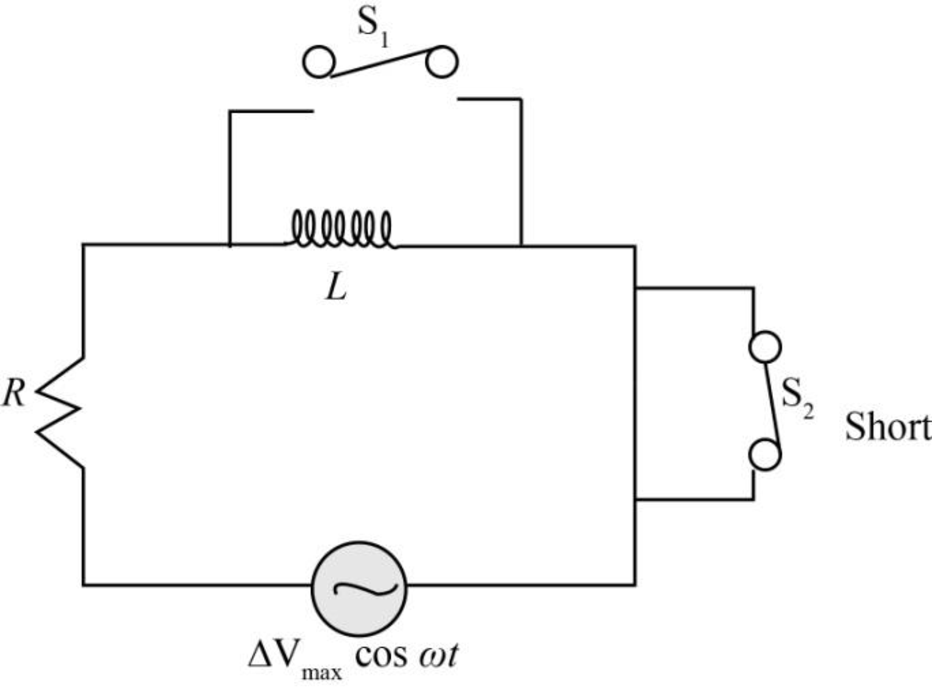
Figure-(2)

In case of inductor circuit, the phase difference between the current and voltage is $90°$.

Write the expression to obtain the time varying voltage source in case $RL$ circuit.

    $\Delta v(t)=\Delta V_{\max }\cos \left(\omega t-\frac{\pi }{2}\right)$

Here, $\Delta v(t)$ is the time varying voltage source, $\Delta V_{\max }$ is the maximum voltage, $\omega$ is the angular frequency and $t$ is the time interval.

Write the expression to obtain the impedance in the circuit.

    $Z=\sqrt{R^2+{\left(\omega L\right)}^2}$

Here, $Z$ is the impedance in the circuit, $R$ is the resistance of the resistor, $L$ is the inductance of the inductor and $\omega$ is the angular frequency.

Write the expression to obtain the current in the circuit as a function of time.

    $i\left(t\right)=\frac{\Delta v\left(t\right)}{Z}$

Here, $i\left(t\right)$ is the current in the circuit as a function of time, $\Delta v\left(t\right)$ is the time varying voltage source and $Z$ is the impedance in the circuit.

Substitute $\Delta V_{\max }\cos \left(\omega t-\frac{\pi }{2}\right)$ for $\Delta v(t)$ and $\sqrt{R^2+{\left(\omega L\right)}^2}$ for $Z$ in the above equation.

    $i\left(t\right)=\frac{\Delta V_{\max }\cos \left(\omega t-\frac{\pi }{2}\right)}{\sqrt{R^2+{\left(\omega L\right)}^2}}$

Conclusion:

Therefore, the current in the circuit as function of time if only switch $1$ is open is $\frac{\Delta V_{\max }\cos \left(\omega t-\frac{\pi }{2}\right)}{\sqrt{R^2+{\left(\omega L\right)}^2}}$.

(d)

To determine

The capacitance of the capacitor when both the switches are closed and the current and voltage are in phase.

Answer to Problem 72AP

The capacitance of the capacitor when both the switches are open and the current and voltage are in phase is $\frac{1}{{\omega }^{2}L}$.

Explanation of Solution

The circuit in which both the switches are open as shown in the figure below.

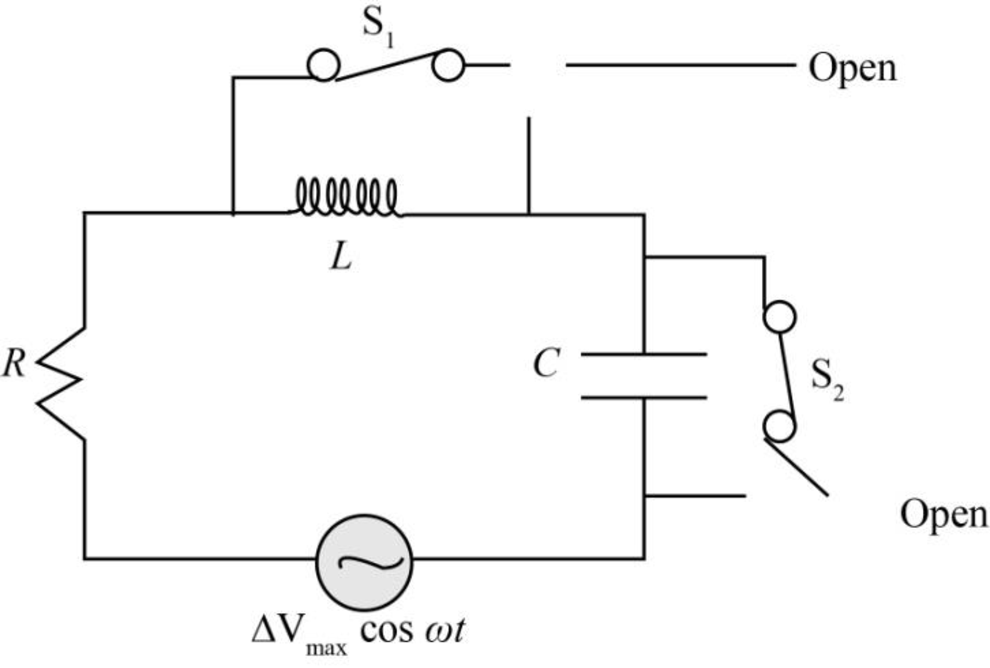
Figure-(3)

Write the expression obtain the impendence of the inductor.

    $X_{\text{L}}=\omega L$

Here, $X_{\text{L}}$ is the impendence of the inductor, $\omega$ is the angular frequency and $L$ is the inductance of the inductor.

Write the expression obtain the impendence of the capacitor.

    $X_{\text{C}}=\frac{1}{\omega C}$

Here, $X_{\text{C}}$ is the impendence of the capacitor, $\omega$ is the angular frequency and $C$ is the capacitance of the capacitor.

When the current and voltage in the circuit are in phase, than the impendence of the inductor and the capacitor are equal.

Write the expression to obtain the relation the capacitance of the capacitor.

    $X_{\text{L}}=X_{\text{C}}$

Here, $X_{\text{L}}$ is the impendence of the inductor and $X_{\text{C}}$ is the impendence of the capacitor.

Substitute $\omega L$ for $X_{\text{L}}$ and $\frac{1}{\omega C}$ for $X_{\text{C}}$ in the above equation.

    $\begin{array}{l}\omega L=\frac{1}{\omega C}\\ C=\frac{1}{{\omega }^{2}L}\end{array}$

Conclusion:

Therefore, the capacitance of the capacitor when both the switches are open and the current and voltage are in phase is $\frac{1}{{\omega }^{2}L}$.

(e)

To determine

The impendence of the circuit when both the switches are open.

Answer to Problem 72AP

The impendence of the circuit when both the switches are open is $R$.

Explanation of Solution

Write the expression when both the switches are open.

    $X_{\text{L}}=X_{\text{C}}$

Here, $X_{\text{L}}$ is the impendence of the inductor and $X_{\text{C}}$ is the impendence of the capacitor.

Write the expression to obtain the impendence of the circuit.

    $Z=\sqrt{R^2+{\left(X_{\text{L}}-X_{\text{C}}\right)}^2}$

Here, $Z$ is the impendence of the circuit, $R$ is the resistance of the resistor, $X_{\text{L}}$ is the impendence of the inductor and $X_{\text{C}}$ is the impendence of the capacitor.

Substitute $X_{\text{L}}$ for $X_{\text{C}}$ in the above equation.

    $\begin{array}{c}Z=\sqrt{R^2+{\left(X_{\text{L}}-X_{\text{L}}\right)}^2}\\ =\sqrt{R^2}\\ =R\end{array}$

Conclusion:

Therefore, the impendence of the circuit when both the switches are open is $R$.

(f)

To determine

The maximum energy stored in the capacitor during the oscillations.

Answer to Problem 72AP

The maximum energy stored in the capacitor during the oscillations is $\frac{1}{2}\frac{\Delta V_{\max }^2}{R^2{\omega }^2{C}^2}$.

Explanation of Solution

Write the expression to obtain the voltage across the capacitor.

    $\Delta V=I_{\max }{X}_{\text{C}}$

Here, $\Delta V$ is the voltage across the capacitor, $I_{\max }$ is the maximum current in the circuit and $X_{\text{C}}$ is the impendence of the capacitor.

Substitute $\frac{1}{\omega C}$ for $X_{\text{C}}$ and $\frac{\Delta V_{\max }}{R}$ for $I_{\max }$ in the above equation.

    $\begin{array}{c}\Delta V=\left(\frac{\Delta V_{\max }}{R}\right)\left(\frac{1}{\omega C}\right)\\ =\frac{\Delta V_{\max }}{R\omega C}\end{array}$

Write the expression to obtain the maximum energy stored in the capacitor.

    $U_{\text{C}}=\frac{1}{2}C{\left(\Delta V\right)}^2$

Here, $U_{\text{C}}$ is the maximum energy stored in the capacitor, $C$ is the capacitance of the capacitor and $\Delta V$ is the voltage across the capacitor.

Substitute $\frac{\Delta V_{\max }}{R\omega C}$ for $\Delta V$ in the above equation.

    $\begin{array}{c}{U}_{\text{C}}=\frac{1}{2}C{\left(\frac{\Delta V_{\max }}{R\omega C}\right)}^2\\ =\frac{1}{2}\frac{\Delta V_{\max }^2}{R^2{\omega }^2{C}^2}\end{array}$

Conclusion:

Therefore, the maximum energy stored in the capacitor during the oscillations is $\frac{1}{2}\frac{\Delta V_{\max }^2}{R^2{\omega }^2{C}^2}$.

(g)

To determine

The maximum energy stored in the inductor during the oscillations.

Answer to Problem 72AP

The maximum energy stored in the inductor during the oscillations is $\frac{1}{2}\frac{L\Delta V_{\max }^2}{R^2}$.

Explanation of Solution

Write the expression to obtain the maximum energy stored in the inductor.

    $U_{\text{L}}=\frac{1}{2}L{\left(I_{\max }\right)}^2$

Here, $U_{\text{L}}$ is the maximum energy stored in the inductor, $L$ is the inductance of the inductor and $I_{\max }$ is the maximum current across the circuit.

Substitute $\frac{\Delta V_{\max }}{R}$ for $I_{\max }$ in the above equation.

    $\begin{array}{c}{U}_{\text{C}}=\frac{1}{2}L{\left(\frac{\Delta V_{\max }}{R}\right)}^2\\ =\frac{1}{2}\frac{L\Delta V_{\max }^2}{R^2}\end{array}$

Conclusion:

Therefore, the maximum energy stored in the inductor during the oscillations is $\frac{1}{2}\frac{L\Delta V_{\max }^2}{R^2}$.

(h)

To determine

The phase difference between the current and the voltage when frequency of the voltage source is doubled.

Answer to Problem 72AP

The phase difference between the current and the voltage when frequency of the voltage source is doubled is ${\tan }^{-1}\left(\frac{2\omega L-\frac{1}{2\omega C}}{R}\right)$.

Explanation of Solution

Write the expression to obtain the phase difference between the current and voltage.

    $\varphi ={\tan }^{-1}\left(\frac{X_{\text{L}}-X_{\text{C}}}{R}\right)$

Here, $\varphi$ is the phase difference between the current and voltage, $X_{\text{L}}$ is the impendence of the inductor, $X_{\text{C}}$ is the impendence of the capacitor and $R$ is the resistance of the resistor.

Substitute $\omega L$ for $X_{\text{L}}$ and $\frac{1}{\omega C}$ for $X_{\text{C}}$ in the above equation.

    $\varphi ={\tan }^{-1}\left(\frac{\omega L-\frac{1}{\omega C}}{R}\right)$

As the frequency of the voltage source is doubled.

Substitute $2\omega$ for $\omega$ in the above equation.

    $\varphi ={\tan }^{-1}\left(\frac{2\omega L-\frac{1}{2\omega C}}{R}\right)$

Conclusion:

Therefore, the phase difference between the current and the voltage when frequency of the voltage source is doubled is ${\tan }^{-1}\left(\frac{2\omega L-\frac{1}{2\omega C}}{R}\right)$.

(i)

To determine

The frequency that makes the inductance reactance one-half the capacitive reactance.

Answer to Problem 72AP

The frequency that makes the inductance reactance one-half the capacitive reactance is $\frac{1}{2\pi }\frac{1}{\sqrt{2LC}}$.

Explanation of Solution

Write the expression to obtain the frequency that makes the inductance reactance one-half the capacitive reactance.

    $X_{\text{L}}=\frac{1}{2}{X}_{\text{C}}$

Here, $X_{\text{L}}$ is the inductive reactance and $X_{\text{C}}$ is the capacitive reactance.

Substitute $2\pi fL$ for $X_{\text{L}}$ and $\frac{1}{2\pi fC}$ for $X_{\text{C}}$ in the above equation.

    $\begin{array}{c}2\pi fL=\frac{1}{2}\left(\frac{1}{2\pi fC}\right)\\ f^2=\frac{1}{8\pi }\frac{1}{LC}\\ f=\frac{1}{2\pi }\frac{1}{\sqrt{2LC}}\end{array}$

Conclusion:

Therefore, the frequency that makes the inductance reactance one-half the capacitive reactance is $\frac{1}{2\pi }\frac{1}{\sqrt{2LC}}$.