DISCRETE MATHEMATICS+ITS APPL. (LL)-W/A
8th Edition
ISBN: 9781260521337
Author: ROSEN
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 3.3, Problem 41E
rcises 41 and 42 deal with the problem of scheduling the most talks possible given the start and end times ofntalks.
- Find the complexity of a brute-force algorithm for scheduling the talks by examining all possible subsets of the talks. [Hint: Use the fact that a set withnelements has
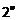subsets.]
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
65% of all violent felons in the prison system are repeat offenders. If 43 violent felons are randomly selected, find the probability that
a. Exactly 28 of them are repeat offenders.
b. At most 28 of them are repeat offenders. c. At least 28 of them are repeat offenders. d. Between 22 and 26 (including 22 and 26) of them are repeat offenders.
(b) Find the (instantaneous) rate of change of y at x = 5.
In the previous part, we found the average rate of change for several intervals of decreasing size starting at x = 5. The instantaneous rate of
change of fat x = 5 is the limit of the average rate of change over the interval [x, x + h] as h approaches 0. This is given by the derivative in the
following limit.
lim
h→0
-
f(x + h) − f(x)
h
The first step to find this limit is to compute f(x + h). Recall that this means replacing the input variable x with the expression x + h in the rule
defining f.
f(x + h) = (x + h)² - 5(x+ h)
=
2xh+h2_
x² + 2xh + h² 5✔
-
5
)x - 5h
Step 4
-
The second step for finding the derivative of fat x is to find the difference f(x + h) − f(x).
-
f(x + h) f(x) =
= (x²
x² + 2xh + h² -
])-
=
2x
+ h² - 5h
])x-5h) - (x² - 5x)
=
]) (2x + h - 5)
Macbook Pro
Evaluate the integral using integration by parts.
Sx² cos
(9x) dx
Chapter 3 Solutions
DISCRETE MATHEMATICS+ITS APPL. (LL)-W/A
Ch. 3.1 - List all the steps used by Algorithm 1 to find the...Ch. 3.1 - Determine which characteristics of an algorithm...Ch. 3.1 - Devise an algorithm that finds the sum of all the...Ch. 3.1 - Describe an algorithm that takes as input a list...Ch. 3.1 - Describe an algorithm that takes as input a list...Ch. 3.1 - Describe an algorithm that takes as input a list...Ch. 3.1 - Describe an algorithm that takes as input a list...Ch. 3.1 - Describe an algorithm that takes as input a list...Ch. 3.1 - Apalindromeis a string that reads the same forward...Ch. 3.1 - Devise an algorithm to computexn, wherexis a real...
Ch. 3.1 - Describe an algorithm that interchanges the values...Ch. 3.1 - cribe an algorithm that uses only assignment...Ch. 3.1 - List all the steps used to search for 9 in the...Ch. 3.1 - List all the steps used to search for 7 in the...Ch. 3.1 - cribe an algorithm that inserts an integerxin the...Ch. 3.1 - Describe an algorithm for finding the smallest...Ch. 3.1 - Describe an algorithm that locates the first...Ch. 3.1 - Describe an algorithm that locates the last...Ch. 3.1 - Describe an algorithm that produces the maximum,...Ch. 3.1 - Describe an algorithm for finding both the largest...Ch. 3.1 - Describe an algorithm that puts the first three...Ch. 3.1 - Prob. 22ECh. 3.1 - Prob. 23ECh. 3.1 - Describe an algorithm that determines whether a...Ch. 3.1 - Describe an algorithm that will count the number...Ch. 3.1 - nge Algorithm 3 so that the binary search...Ch. 3.1 - Theternary search algorithmlocates an element in a...Ch. 3.1 - Specify the steps of an algorithm that locates an...Ch. 3.1 - Devise an algorithm that finds a mode in a list of...Ch. 3.1 - Devise an algorithm that finds all modes. (Recall...Ch. 3.1 - Two strings areanagramsif each can be formed from...Ch. 3.1 - ennreal numbersx1,x2,...,xn , find the two that...Ch. 3.1 - Devise an algorithm that finds the first term of a...Ch. 3.1 - Prob. 34ECh. 3.1 - Prob. 35ECh. 3.1 - Use the bubble sort to sort 6, 2, 3, 1, 5, 4,...Ch. 3.1 - Use the bubble sort to sort 3, 1, 5, 7, 4, showing...Ch. 3.1 - Use the bubble sort to sortd,f,k,m,a,b, showing...Ch. 3.1 - Adapt the bubble sort algorithm so that it stops...Ch. 3.1 - Use the insertion sort to sort the list in...Ch. 3.1 - Use the insertion sort to sort the list in...Ch. 3.1 - Use the insertion sort to sort the list in...Ch. 3.1 - Sort these lists using the selection sort....Ch. 3.1 - Write the selection sort algorithm in pseudocode.Ch. 3.1 - Describe an algorithm based on the linear search...Ch. 3.1 - Describe an algorithm based on the binary search...Ch. 3.1 - How many comparisons does the insertion sort use...Ch. 3.1 - How many comparisons does the insertion sort use...Ch. 3.1 - Show all the steps used by the binary insertion...Ch. 3.1 - Compare the number of comparisons used by the...Ch. 3.1 - Prob. 51ECh. 3.1 - Devise a variation of the insertion sort that uses...Ch. 3.1 - Prob. 53ECh. 3.1 - List all the steps the naive string matcher uses...Ch. 3.1 - List all the steps the naive string matcher uses...Ch. 3.1 - Use the cashier’s algorithm to make change using...Ch. 3.1 - Use the cashier’s algorithm to make change using...Ch. 3.1 - Use the cashier’s algorithm to make change using...Ch. 3.1 - Prob. 59ECh. 3.1 - Show that if there were a coin worth 12 cents, the...Ch. 3.1 - Prob. 61ECh. 3.1 - Prob. 62ECh. 3.1 - Devise a greedy algorithm that determines the...Ch. 3.1 - Suppose we have three menm1,m2, andm3and three...Ch. 3.1 - Write the deferred acceptance algorithm in...Ch. 3.1 - Prob. 66ECh. 3.1 - Prob. 67ECh. 3.1 - Prob. 68ECh. 3.1 - Prove that the Boyer-Moore majority vote algorithm...Ch. 3.1 - Show that the problem of determining whether a...Ch. 3.1 - Prob. 71ECh. 3.1 - Show that the problem of deciding whether a...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Prob. 11ECh. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - ermine whetherx3isO(g(x))for each of these...Ch. 3.2 - Explain what it means for a function to be 0(1)Ch. 3.2 - w that iff(x)isO(x)thenf(x)isO(x2).Ch. 3.2 - Suppose thatf(x),g(x), andh(x)are functions such...Ch. 3.2 - kbe a positive integer. Show...Ch. 3.2 - Prob. 19ECh. 3.2 - To simplify:(3a5)3 27a15 Given information:(3a5)3....Ch. 3.2 - ange the functionsn, 1000 logn,nlogn,2n!,2n,3n,...Ch. 3.2 - Arrange the...Ch. 3.2 - Suppose that you have two different algorithms for...Ch. 3.2 - Suppose that you have two different algorithms for...Ch. 3.2 - Give as good a big-Oestimate as possible for each...Ch. 3.2 - e a big-Oestimate for each of these functions. For...Ch. 3.2 - Give a big-Oestimate for each of these functions....Ch. 3.2 - each function in Exercise 1, determine whether...Ch. 3.2 - Prob. 29ECh. 3.2 - Show that each of these pairs of functions are of...Ch. 3.2 - Prob. 31ECh. 3.2 - w thatf(x)andg(x)are functions from the set of...Ch. 3.2 - Prob. 33ECh. 3.2 - Show that3x2+x+1is(3x2)by directly finding the...Ch. 3.2 - Prob. 35ECh. 3.2 - lain what it means for a function to be(1).Ch. 3.2 - Prob. 37ECh. 3.2 - Give a big-Oestimate of the product of the...Ch. 3.2 - Prob. 39ECh. 3.2 - Prob. 40ECh. 3.2 - Prob. 41ECh. 3.2 - pose thatf(x)isO(g(x)). Does it follow...Ch. 3.2 - Prob. 43ECh. 3.2 - pose thatf(x),g(x), andh(x)are functions such...Ch. 3.2 - Prob. 45ECh. 3.2 - Prob. 46ECh. 3.2 - Prob. 47ECh. 3.2 - ress the relationshipf(x)is(g(x))using a picture....Ch. 3.2 - Prob. 49ECh. 3.2 - w that iff(x)=anxn+an1xn1++a1x+a0,...Ch. 3.2 - Prob. 51ECh. 3.2 - Prob. 52ECh. 3.2 - Prob. 53ECh. 3.2 - w thatx5y3+x4y4+x3y5is(x3y3).Ch. 3.2 - w thatxyisO(xy).Ch. 3.2 - w thatxyis(xy).Ch. 3.2 - Prob. 57ECh. 3.2 - Prob. 58ECh. 3.2 - Prob. 59ECh. 3.2 - Prob. 60ECh. 3.2 - Prob. 61ECh. 3.2 - (Requires calculus) Prove or disprove that (2n)!...Ch. 3.2 - Prob. 63ECh. 3.2 - Prob. 64ECh. 3.2 - Prob. 65ECh. 3.2 - Prob. 66ECh. 3.2 - Prob. 67ECh. 3.2 - Prob. 68ECh. 3.2 - Prob. 69ECh. 3.2 - Prob. 70ECh. 3.2 - Prob. 71ECh. 3.2 - Prob. 72ECh. 3.2 - Show thatnlognisO(logn!).Ch. 3.2 - Prob. 74ECh. 3.2 - Prob. 75ECh. 3.2 - Prob. 76ECh. 3.2 - (Requires calculus) For each of these pairs of...Ch. 3.3 - Give a big-Oestimate for the number of operations...Ch. 3.3 - Give a big-Oestimate for the number additions used...Ch. 3.3 - Give a big-Oestimate for the number of operations,...Ch. 3.3 - Give a big-Oestimate for the number of operations,...Ch. 3.3 - Prob. 5ECh. 3.3 - Use pseudocode to describe the algorithm that puts...Ch. 3.3 - Suppose that an element is known to be among the...Ch. 3.3 - Prob. 8ECh. 3.3 - Give a big-Oestimate for the number of comparisons...Ch. 3.3 - Show that this algorithm determines the number of...Ch. 3.3 - pose we havensubsetsS1,S2, ...,Snof the set {1, 2,...Ch. 3.3 - Consider the following algorithm, which takes as...Ch. 3.3 - The conventional algorithm for evaluating a...Ch. 3.3 - re is a more efficient algorithm (in terms of the...Ch. 3.3 - t is the largestnfor which one can solve within...Ch. 3.3 - What is the largestnfor which one can solve within...Ch. 3.3 - What is the largestnfor which one can solve within...Ch. 3.3 - How much time does an algorithm take to solve a...Ch. 3.3 - Prob. 19ECh. 3.3 - What is the effect in the time required to solve a...Ch. 3.3 - Prob. 21ECh. 3.3 - Determine the least number of comparisons, or...Ch. 3.3 - Analyze the average-case performance of the linear...Ch. 3.3 - An algorithm is calledoptimalfor the solution of a...Ch. 3.3 - Describe the worst-case time complexity, measured...Ch. 3.3 - Prob. 26ECh. 3.3 - Prob. 27ECh. 3.3 - Prob. 28ECh. 3.3 - Analyze the worst-case time complexity of the...Ch. 3.3 - Analyze the worst-case time complexity of the...Ch. 3.3 - Analyze the worst-case time complexity of the...Ch. 3.3 - Prob. 32ECh. 3.3 - Prob. 33ECh. 3.3 - Prob. 34ECh. 3.3 - Determine a big-O estimate for the worst-case...Ch. 3.3 - Determine the number of character comparisons used...Ch. 3.3 - Determine a big-Oestimate of the number of...Ch. 3.3 - Prob. 38ECh. 3.3 - Prob. 39ECh. 3.3 - Show that the greedy algorithm for making change...Ch. 3.3 - rcises 41 and 42 deal with the problem of...Ch. 3.3 - rcises 41 and 42 deal with the problem of...Ch. 3.3 - Prob. 43ECh. 3.3 - Prob. 44ECh. 3.3 - Prob. 45ECh. 3.3 - Prob. 46ECh. 3.3 - Prob. 47ECh. 3.3 - Prob. 48ECh. 3.3 - Prob. 49ECh. 3 - Define the termalgorithm. What are the different...Ch. 3 - Describe, using English, an algorithm for finding...Ch. 3 - Prob. 3RQCh. 3 - Prob. 4RQCh. 3 - Prob. 5RQCh. 3 - Define what the worst-case time complexity,...Ch. 3 - Prob. 7RQCh. 3 - Describe the bubble sort algorithm. Use the bubble...Ch. 3 - Describe the insertion sort algorithm. Use the...Ch. 3 - Explain the concept of a greedy algorithm. Provide...Ch. 3 - Prob. 11RQCh. 3 - Describe an algorithm for locating the last...Ch. 3 - Prob. 2SECh. 3 - Give an algorithm to determine whether a bit...Ch. 3 - Suppose that a list contains integers that are in...Ch. 3 - Prob. 5SECh. 3 - Prob. 6SECh. 3 - Prob. 7SECh. 3 - Prob. 8SECh. 3 - Prob. 9SECh. 3 - Prob. 10SECh. 3 - Show the steps used by the shaker sort to sort the...Ch. 3 - Express the shaker sort in pseudocode.Ch. 3 - Prob. 13SECh. 3 - Prob. 14SECh. 3 - Prob. 15SECh. 3 - w that8x3+12x+100logxisO(x3).Ch. 3 - Prob. 17SECh. 3 - Prob. 18SECh. 3 - Prob. 19SECh. 3 - w thatnnis notO(n!).Ch. 3 - Prob. 21SECh. 3 - Prob. 22SECh. 3 - Prob. 23SECh. 3 - Prob. 24SECh. 3 - Arrange the...Ch. 3 - Prob. 26SECh. 3 - Prob. 27SECh. 3 - Show that if the denominations of coins arec0,c1,...Ch. 3 - Prob. 29SECh. 3 - Prob. 30SECh. 3 - Prob. 31SECh. 3 - Show that the deferred acceptance algorithm given...Ch. 3 - Prob. 33SECh. 3 - Show that when woman do the proposing in the...Ch. 3 - Prob. 35SECh. 3 - Prob. 36SECh. 3 - Prob. 37SECh. 3 - Prob. 38SECh. 3 - Prob. 39SECh. 3 - Prob. 40SECh. 3 - Prob. 41SECh. 3 - Exercises 4246 we will study the problem of load...Ch. 3 - Prob. 43SECh. 3 - Prob. 44SECh. 3 - Prob. 45SECh. 3 - Prove that the algorithm from Exercise 44 is a...Ch. 3 - Prob. 1CPCh. 3 - Prob. 2CPCh. 3 - Prob. 3CPCh. 3 - Prob. 4CPCh. 3 - Prob. 5CPCh. 3 - Prob. 6CPCh. 3 - Prob. 7CPCh. 3 - Given an integern, use the cashier’s algorithm to...Ch. 3 - Prob. 9CPCh. 3 - Prob. 10CPCh. 3 - Prob. 11CPCh. 3 - Prob. 1CAECh. 3 - Prob. 2CAECh. 3 - Using a generator of random orderings of the...Ch. 3 - Prob. 4CAECh. 3 - Write a program that animates the progress of all...Ch. 3 - Examine the history of the wordalgorithmand...Ch. 3 - Prob. 2WPCh. 3 - Explain how sorting algorithms can be classified...Ch. 3 - Prob. 4WPCh. 3 - Prob. 5WPCh. 3 - Prob. 6WPCh. 3 - Describe the historic trends in how quickly...Ch. 3 - Develop a detailed list of algorithmic paradigms...Ch. 3 - Explain what the Turing Award is and describe the...Ch. 3 - Prob. 10WPCh. 3 - Prob. 11WPCh. 3 - Describe six different NP-complete problems.Ch. 3 - Prob. 13WP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Let f be defined as follows. y = f(x) = x² - 5x (a) Find the average rate of change of y with respect to x in the following intervals. from x = 4 to x = 5 from x = 4 to x = 4.5 from x = 4 to x = 4.1 (b) Find the (instantaneous) rate of change of y at x = 4. Need Help? Read It Master Itarrow_forwardDetermine whether the inverse of f(x)=x^4+2 is a function. Then, find the inverse.arrow_forwardVelocity of a Ball Thrown into the Air The position function of an object moving along a straight line is given by s = f(t). The average velocity of the object over the time interval [a, b] is the average rate of change of f over [a, b]; its (instantaneous) velocity at t = a is the rate of change of f at a. A ball is thrown straight up with an initial velocity of 128 ft/sec, so that its height (in feet) after t sec is given by s = f(t) = 128t - 16t². (a) What is the average velocity of the ball over the following time intervals? [3,4] [3, 3.5] [3, 3.1] ft/sec ft/sec ft/sec (b) What is the instantaneous velocity at time t = 3? ft/sec (c) What is the instantaneous velocity at time t = 7? ft/sec Is the ball rising or falling at this time? O rising falling (d) When will the ball hit the ground? t = sec Need Help? Read It Watch Itarrow_forward
- Find the slope of the tangent line to the graph of the function at the given point. f(x) = -4x + 5 at (-1, 9) m Determine an equation of the tangent line. y = Need Help? Read It Watch It SUBMIT ANSWERarrow_forwardFind the slope of the tangent line to the graph of the function at the given point. f(x) = 5x-4x² at (-1, -9) m Determine an equation of the tangent line. y = Need Help? Read It Master It SUBMIT ANSWERarrow_forwardy = log 5 – x2 - 4 00arrow_forward
- For what value of A and B the function f(x) will be continuous everywhere for the given definition?..arrow_forwardPlease fill in the rest of the steps of the proof of Thm 2.5. Show how "Repeating this step with n-1,n-2,...,2 in place of n" gives us the desired result.arrow_forward2. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.4.006.MI. Use the Table of Integrals to evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) 7y2 y² 11 dy Need Help? Read It Master It SUBMIT ANSWER 3. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.4.009. Use the Table of Integrals to evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) tan³(12/z) dz Need Help? Read It Watch It SUBMIT ANSWER 4. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.4.014. Use the Table of Integrals to evaluate the integral. (Use C for the constant of integration.) 5 sinб12x dx Need Help? Read Itarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebraic Complexity with Less Relations; Author: The University of Chicago;https://www.youtube.com/watch?v=ZOKM1JPz650;License: Standard Youtube License
Strassen's Matrix Multiplication - Divide and Conquer - Analysis of Algorithm; Author: Ekeeda;https://www.youtube.com/watch?v=UnpySHwAJsQ;License: Standard YouTube License, CC-BY
Trigonometric Equations with Complex Numbers | Complex Analysis #6; Author: TheMathCoach;https://www.youtube.com/watch?v=zdD8Dab1T2Y;License: Standard YouTube License, CC-BY