Pearson eText for Finite Mathematics & Its Applications -- Instant Access (Pearson+)
12th Edition
ISBN: 9780137442966
Author: Larry Goldstein, David Schneider
Publisher: PEARSON+
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 3.3, Problem 16E
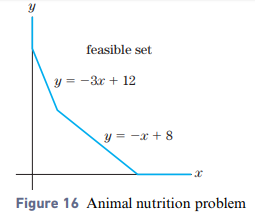
Nutrition—-Animal Refer to Exercises 3.2, Problem 8. How many cans of each dog food should he give to his dog each day to provide the minimum requirements with the least amount of sodium? What is the least amount of sodium? (See the graph of the feasible set in Fig. 16.)
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Answers
What is a solution to a differential equation? We said that a differential equation is an equation that
describes the derivative, or derivatives, of a function that is unknown to us. By a solution to a differential
equation, we mean simply a function that satisfies this description.
2. Here is a differential equation which describes an unknown position function s(t):
ds
dt
318
4t+1,
ds
(a) To check that s(t) = 2t2 + t is a solution to this differential equation, calculate
you really do get 4t +1.
and check that
dt'
(b) Is s(t) = 2t2 +++ 4 also a solution to this differential equation?
(c) Is s(t)=2t2 + 3t also a solution to this differential equation?
ds
1
dt
(d) To find all possible solutions, start with the differential equation = 4t + 1, then move dt to the
right side of the equation by multiplying, and then integrate both sides. What do you get?
(e) Does this differential equation have a unique solution, or an infinite family of solutions?
these are solutions to a tutorial that was done and im a little lost. can someone please explain to me how these iterations function, for example i Do not know how each set of matrices produces a number if someine could explain how its done and provide steps it would be greatly appreciated thanks.
Chapter 3 Solutions
Pearson eText for Finite Mathematics & Its Applications -- Instant Access (Pearson+)
Ch. 3.1 - Graph the inequality 3xy3.Ch. 3.1 - Graph the feasible set for the system of...Ch. 3.1 - In Exercises 1-4, state whether the inequality is...Ch. 3.1 - In Exercises 1-4, state whether the inequality is...Ch. 3.1 - In Exercises 1-4, state whether the inequality is...Ch. 3.1 - In Exercises 1-4, state whether the inequality is...Ch. 3.1 - In Exercises 5-7, solve for x, 2x53Ch. 3.1 - Prob. 6ECh. 3.1 - In Exercises 5-7, solve for x,
7.
Ch. 3.1 - Which of the following results from solving x+13...
Ch. 3.1 - Prob. 9ECh. 3.1 - In Exercises 9-14, write the linear inequality in...Ch. 3.1 - In Exercises 9-14, write the linear inequality in...Ch. 3.1 - In Exercises 9-14, write the linear inequality in...Ch. 3.1 - In Exercises 9-14, write the linear inequality in...Ch. 3.1 - In Exercises 9-14, write the linear inequality in...Ch. 3.1 - In Exercises 15-22, determine whether or not the...Ch. 3.1 - In Exercises 15-22, determine whether or not the...Ch. 3.1 - In Exercises 15-22, determine whether or not the...Ch. 3.1 - In Exercises 15-22, determine whether or not the...Ch. 3.1 - In Exercises 15-22, determine whether or not the...Ch. 3.1 - In Exercises 15-22, determine whether or not the...Ch. 3.1 - Prob. 21ECh. 3.1 - Prob. 22ECh. 3.1 - In Exercises 23-26, graph the given inequality by...Ch. 3.1 - In Exercises 23-26, graph the given inequality by...Ch. 3.1 - Prob. 25ECh. 3.1 - In Exercises 23-26, graph the given inequality by...Ch. 3.1 - In Exercises 27-30, give the linear inequality...Ch. 3.1 - In Exercises 27-30, give the linear inequality...Ch. 3.1 - In Exercises 27-30, give the linear inequality...Ch. 3.1 - In Exercises 27-30, give the linear inequality...Ch. 3.1 - In Exercises 31-42, graph the given inequality....Ch. 3.1 - In Exercises 31-42, graph the given...Ch. 3.1 - In Exercises 31-42, graph the given inequality. x2Ch. 3.1 - In Exercises 31-42, graph the given inequality. x0Ch. 3.1 - In Exercises 31-42, graph the given...Ch. 3.1 - In Exercises 31-42, graph the given inequality....Ch. 3.1 - In Exercises 31-42, graph the given inequality....Ch. 3.1 - In Exercises 31-42, graph the given...Ch. 3.1 - In Exercises 31-42, graph the given inequality....Ch. 3.1 - In Exercises 31-42, graph the given...Ch. 3.1 - In Exercises 31-42, graph the given inequality....Ch. 3.1 - In Exercises 31-42, graph the given inequality....Ch. 3.1 - In Exercises 43-48, graph the feasible set for the...Ch. 3.1 - In Exercises 43-48, graph the feasible set for the...Ch. 3.1 - In Exercises 43-48, graph the feasible set for the...Ch. 3.1 - In Exercises 43-48, graph the feasible set for the...Ch. 3.1 - In Exercises 43-48, graph the feasible set for the...Ch. 3.1 - In Exercises 43-48, graph the feasible set for the...Ch. 3.1 - In Exercises 49-52, determine whether the given...Ch. 3.1 - In Exercises 49-52, determine whether the given...Ch. 3.1 - In Exercises 49-52, determine whether the given...Ch. 3.1 - In Exercises 49-52, determine whether the given...Ch. 3.1 - In Exercises 52-56, determine whether the given...Ch. 3.1 - In Exercises 52-56, determine whether the given...Ch. 3.1 - In Exercises 52-56, determine whether the given...Ch. 3.1 - In Exercises 52-56, determine whether the given...Ch. 3.1 - Give a system of inequalities for which the graph...Ch. 3.1 - The shaded region in Fig. 9 is bounded by four...Ch. 3.1 - The shaded region in Fig. 10 is bounded by four...Ch. 3.1 - Which quadrant if Fig. 11 contains no points that...Ch. 3.1 - Graph the line 4x2y=7. (a) Locate the point on the...Ch. 3.1 - 62. Graph the line
(a) Locate the point on the...Ch. 3.1 - Display the feasible set in Exercise 47.Ch. 3.1 - Display the feasible set in Exercise 48.Ch. 3.2 - 1. Determine whether the following points are in...Ch. 3.2 - A physical fitness enthusiast decides to devote...Ch. 3.2 - Prob. 1ECh. 3.2 - Prob. 2ECh. 3.2 - In Exercises 14, determine whether the given point...Ch. 3.2 - Prob. 4ECh. 3.2 - Manufacturing Consider the furniture manufacturing...Ch. 3.2 - 6. Manufacturing Consider the furniture...Ch. 3.2 - Packaging Joes Confectionary puts together two...Ch. 3.2 - Nutrition-Animal Mr. Holloway decides to feed his...Ch. 3.2 - Shipping A truck traveling from New York to...Ch. 3.2 - 10. Mining A coal company owns mines in two...Ch. 3.2 - 11. Exam Strategy A student is taking an exam...Ch. 3.2 - 12. Political Campaign—Resource Allocation A local...Ch. 3.2 - Nutrition-Dairy Cows A dairy farmer concludes that...Ch. 3.2 - Manufacturing-Resource Allocation A clothing...Ch. 3.3 - The feasible set for the nutrition problem of...Ch. 3.3 - 2. Rework the nutrition problem, assuming that...Ch. 3.3 - For each of the feasible sets in Exercises 1–4,...Ch. 3.3 - For each of the feasible sets in Exercises 14,...Ch. 3.3 - For each of the feasible sets in Exercises 14,...Ch. 3.3 - Prob. 4ECh. 3.3 - In Exercises 58, find the values of x and y that...Ch. 3.3 - In Exercises 58, find the values of x and y that...Ch. 3.3 - In Exercises 58, find the values of x and y that...Ch. 3.3 - In Exercises 5–8, find the values of x and y that...Ch. 3.3 - In Exercises 9–12, find the values of x and y that...Ch. 3.3 - In Exercises 9–12, find the values of x and y that...Ch. 3.3 - In Exercises 9–12, find the values of x and y that...Ch. 3.3 - In Exercises 9–12, find the values of x and y that...Ch. 3.3 - 13. Nutrition—People Consider the nutrition...Ch. 3.3 - 14. Nutrition—People Consider the nutrition...Ch. 3.3 - 15. Packaging Refer to Exercises 3.2, Problem 7....Ch. 3.3 - Nutrition-Animal Refer to Exercises 3.2, Problem...Ch. 3.3 - 17. Shipping Refer to Exercises 3.2, Problem 9....Ch. 3.3 - 18. Mining Refer to Exercises 3.2, Problem 10....Ch. 3.3 - Exam Strategy Refer to Exercises 3.2, Problem 11....Ch. 3.3 - Political Campaign-Resource Allocation Refer to...Ch. 3.3 - 21. Nutrition—Dairy Cows Refer to Exercises 3.2,...Ch. 3.3 - Manufacturing-Resource Allocation Refer to...Ch. 3.3 - Prob. 23ECh. 3.3 - Prob. 24ECh. 3.3 - In Exercises 25–32, find the optimal value for the...Ch. 3.3 - In Exercises 25–32, find the optimal value for the...Ch. 3.3 - In Exercises 2532, find the optimal value for the...Ch. 3.3 - In Exercises 25–32, find the optimal value for the...Ch. 3.3 - In Exercises 25–32, find the optimal value for the...Ch. 3.3 - In Exercises 25–32, find the optimal value for the...Ch. 3.3 - In Exercises 2532, find the optimal value for the...Ch. 3.3 - In Exercises 25–32, find the optimal value for the...Ch. 3.3 - 33. Manufacturing—Resource Allocation Infotron,...Ch. 3.3 - 34. Manufacturing—Production Planning An...Ch. 3.3 - Agriculture-Crop Planning A farmer has 100 acres...Ch. 3.3 - 36. Manufacturing—Resource Allocation A company...Ch. 3.3 - 37. Manufacturing The E-JEM Company produces two...Ch. 3.3 - Refining A refinery has two smelters that extract...Ch. 3.3 - 39. Nutrition—People A nutritionist, working for...Ch. 3.3 - 40. Construction—Resource Allocation A contractor...Ch. 3.3 - 41. Packaging—Product Mix The Beautiful Day Fruit...Ch. 3.3 - 42. Manufacturing—Resource Allocation The Bluejay...Ch. 3.3 - Agriculture-Crop Planning Suppose that the farmer...Ch. 3.3 - 44. Nutrition Pavan wants to add a sliced carrot...Ch. 3.3 - Packaging A small candy shop makes a special Cupid...Ch. 3.3 - Prob. 46ECh. 3.3 - 47. Packaging A bath shop sells two different gift...Ch. 3.3 - Packaging A florist offers two types of Thank You...Ch. 3.3 - Consider the following linear programming problem:...Ch. 3.3 - Consider the following linear programming problem:...Ch. 3.3 - Prob. 51ECh. 3.3 - Use Excel or Wolfram| Alpha to solve Exercise 26.Ch. 3.4 - Problems 1–3 refer to Example 1. Translate the...Ch. 3.4 - Problems 13 refer to Example 1. Translate the...Ch. 3.4 - Problems 13 refer to Example 1. Translate the...Ch. 3.4 - A linear programming problem has objective...Ch. 3.4 - 1. Figure 10(a) shows the feasible set of the...Ch. 3.4 - Figure 10(b) shows the feasible set of the...Ch. 3.4 - Consider the feasible set in Fig. 11, where three...Ch. 3.4 - Consider the feasible set in Fig. 11, where three...Ch. 3.4 - Consider the feasible set in Fig. 11, where three...Ch. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Consider the feasible set in Fig. 12, where three...Ch. 3.4 - Consider the feasible set in Fig. 12, where three...Ch. 3.4 - Consider the feasible set in Fig. 12, where three...Ch. 3.4 - Consider the feasible set in Fig. 13. For what...Ch. 3.4 - Prob. 12ECh. 3.4 - Nutrition-Animal Mr. Smith decides to feed his pet...Ch. 3.4 - Oil Production An oil company owns two refineries....Ch. 3.4 - Investment Planning Mr. Jones has $9000 to invest...Ch. 3.4 - Shipping-Product Mix A produce dealer in Florida...Ch. 3.4 - 17. Transportation—Shipping A foreign-car...Ch. 3.4 - Transportation-Shipping Consider the foreign-car...Ch. 3.4 - Manufacturing-Production Planning An oil refinery...Ch. 3.4 - 20. Manufacturing—Production Planning Suppose that...Ch. 3.4 - 21. Shipping—Resource Allocation A shipping...Ch. 3.4 - Shipping-Resource Allocation Suppose that the...Ch. 3.4 - 23. Transportation—Shipping A major coffee...Ch. 3.4 - Transportation-Shipping Consider the coffee...Ch. 3.4 - 25. Packaging—Product Mix A pet store sells three...Ch. 3.4 - Prob. 26ECh. 3.4 - 27. Refer to Fig. 6. As the lines of constant...Ch. 3.4 - Figure 16 shows the feasible set for the nutrition...Ch. 3.4 - Consider the feasible set in Fig. 17(a). In...Ch. 3.4 - Consider the feasible set in Fig. 17(a). In...Ch. 3.4 - Consider the feasible set in Fig. 17(a). In...Ch. 3.4 - Consider the feasible set in Fig. 17(a). In...Ch. 3.4 - Consider the feasible set in Fig. 17(a). In...Ch. 3.4 - Consider the feasible set in Fig. 17(a). In...Ch. 3.4 - Consider the feasible set in Fig. 17(a). In...Ch. 3.4 - Consider the feasible set in Fig. 17(a). In...Ch. 3.4 - Prob. 37ECh. 3 - State the inequality properties for addition,...Ch. 3 - What are the general forms of a linear inequality...Ch. 3 - Prob. 3FCCECh. 3 - 4. What is meant by the feasible set of a system...Ch. 3 - Prob. 5FCCECh. 3 - Prob. 6FCCECh. 3 - Prob. 7FCCECh. 3 - Prob. 8FCCECh. 3 - 9. Give a procedure for solving a linear...Ch. 3 - Prob. 1RECh. 3 - 2. Graph the linear inequality.
Ch. 3 - 3. Write the inequality whose graph is the...Ch. 3 - 4. Travel—Resource Allocation Terrapin Airlines...Ch. 3 - Nutrition-People A nutritionist is designing a new...Ch. 3 - Prob. 6RECh. 3 - Packaging-Product Mix A confectioner makes two...Ch. 3 - Prob. 8RECh. 3 - Packaging-Resource Allocation A computer company...Ch. 3 - Transportation-Shipping An appliance company has...Ch. 3 - Prob. 11RECh. 3 - Prob. 12RECh. 3 - Prob. 13RECh. 3 - Prob. 14RECh. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - When mathematicians are presented with a linear...Ch. 3 - When mathematicians are presented with a linear...Ch. 3 - When mathematicians are presented with a linear...Ch. 3 - When mathematicians are presented with a linear...Ch. 3 - When mathematicians are presented with a linear...Ch. 3 - When mathematicians are presented with a linear...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Q1) Classify the following statements as a true or false statements a. Any ring with identity is a finitely generated right R module.- b. An ideal 22 is small ideal in Z c. A nontrivial direct summand of a module cannot be large or small submodule d. The sum of a finite family of small submodules of a module M is small in M A module M 0 is called directly indecomposable if and only if 0 and M are the only direct summands of M f. A monomorphism a: M-N is said to split if and only if Ker(a) is a direct- summand in M & Z₂ contains no minimal submodules h. Qz is a finitely generated module i. Every divisible Z-module is injective j. Every free module is a projective module Q4) Give an example and explain your claim in each case a) A module M which has two composition senes 7 b) A free subset of a modale c) A free module 24 d) A module contains a direct summand submodule 7, e) A short exact sequence of modules 74.arrow_forward************* ********************************* Q.1) Classify the following statements as a true or false statements: a. If M is a module, then every proper submodule of M is contained in a maximal submodule of M. b. The sum of a finite family of small submodules of a module M is small in M. c. Zz is directly indecomposable. d. An epimorphism a: M→ N is called solit iff Ker(a) is a direct summand in M. e. The Z-module has two composition series. Z 6Z f. Zz does not have a composition series. g. Any finitely generated module is a free module. h. If O→A MW→ 0 is short exact sequence then f is epimorphism. i. If f is a homomorphism then f-1 is also a homomorphism. Maximal C≤A if and only if is simple. Sup Q.4) Give an example and explain your claim in each case: Monomorphism not split. b) A finite free module. c) Semisimple module. d) A small submodule A of a module N and a homomorphism op: MN, but (A) is not small in M.arrow_forwardProve that Σ prime p≤x p=3 (mod 10) 1 Ρ = for some constant A. log log x + A+O 1 log x "arrow_forward
- Prove that, for x ≥ 2, d(n) n2 log x = B ― +0 X (금) n≤x where B is a constant that you should determine.arrow_forwardProve that, for x ≥ 2, > narrow_forwardI need diagram with solutionsarrow_forwardT. Determine the least common denominator and the domain for the 2x-3 10 problem: + x²+6x+8 x²+x-12 3 2x 2. Add: + Simplify and 5x+10 x²-2x-8 state the domain. 7 3. Add/Subtract: x+2 1 + x+6 2x+2 4 Simplify and state the domain. x+1 4 4. Subtract: - Simplify 3x-3 x²-3x+2 and state the domain. 1 15 3x-5 5. Add/Subtract: + 2 2x-14 x²-7x Simplify and state the domain.arrow_forwardQ.1) Classify the following statements as a true or false statements: Q a. A simple ring R is simple as a right R-module. b. Every ideal of ZZ is small ideal. very den to is lovaginz c. A nontrivial direct summand of a module cannot be large or small submodule. d. The sum of a finite family of small submodules of a module M is small in M. e. The direct product of a finite family of projective modules is projective f. The sum of a finite family of large submodules of a module M is large in M. g. Zz contains no minimal submodules. h. Qz has no minimal and no maximal submodules. i. Every divisible Z-module is injective. j. Every projective module is a free module. a homomorp cements Q.4) Give an example and explain your claim in each case: a) A module M which has a largest proper submodule, is directly indecomposable. b) A free subset of a module. c) A finite free module. d) A module contains no a direct summand. e) A short split exact sequence of modules.arrow_forward1 2 21. For the matrix A = 3 4 find AT (the transpose of A). 22. Determine whether the vector @ 1 3 2 is perpendicular to -6 3 2 23. If v1 = (2) 3 and v2 = compute V1 V2 (dot product). .arrow_forward7. Find the eigenvalues of the matrix (69) 8. Determine whether the vector (£) 23 is in the span of the vectors -0-0 and 2 2arrow_forward1. Solve for x: 2. Simplify: 2x+5=15. (x+3)² − (x − 2)². - b 3. If a = 3 and 6 = 4, find (a + b)² − (a² + b²). 4. Solve for x in 3x² - 12 = 0. -arrow_forward5. Find the derivative of f(x) = 6. Evaluate the integral: 3x3 2x²+x— 5. - [dz. x² dx.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Solve ANY Optimization Problem in 5 Steps w/ Examples. What are they and How do you solve them?; Author: Ace Tutors;https://www.youtube.com/watch?v=BfOSKc_sncg;License: Standard YouTube License, CC-BY
Types of solution in LPP|Basic|Multiple solution|Unbounded|Infeasible|GTU|Special case of LP problem; Author: Mechanical Engineering Management;https://www.youtube.com/watch?v=F-D2WICq8Sk;License: Standard YouTube License, CC-BY
Optimization Problems in Calculus; Author: Professor Dave Explains;https://www.youtube.com/watch?v=q1U6AmIa_uQ;License: Standard YouTube License, CC-BY
Introduction to Optimization; Author: Math with Dr. Claire;https://www.youtube.com/watch?v=YLzgYm2tN8E;License: Standard YouTube License, CC-BY