
Pearson eText for Finite Mathematics & Its Applications -- Instant Access (Pearson+)
12th Edition
ISBN: 9780137442966
Author: Larry Goldstein, David Schneider
Publisher: PEARSON+
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 3.3, Problem 5E
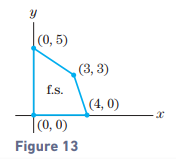
In Exercises 5–8, find the values of x and y that maximize the given objective function for the feasible set in Fig. 13.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Can you cut the 12 glass triangles from a sheet of glass that is 4 feet by 8 feet? If so, how can it be done?
Can you cut 12 glass triangles from a sheet of glass that is 4 feet by 8 feet? If so, draw a diagram of how it can be done.
Use the method of undetermined coefficients to solve the given nonhomogeneous system.
x-()*+(5)
=
1 3
3 1
X+
t +3
-1
-2t
1
x(t)
=
º1 1
e
+021
e
+
Chapter 3 Solutions
Pearson eText for Finite Mathematics & Its Applications -- Instant Access (Pearson+)
Ch. 3.1 - Graph the inequality 3xy3.Ch. 3.1 - Graph the feasible set for the system of...Ch. 3.1 - In Exercises 1-4, state whether the inequality is...Ch. 3.1 - In Exercises 1-4, state whether the inequality is...Ch. 3.1 - In Exercises 1-4, state whether the inequality is...Ch. 3.1 - In Exercises 1-4, state whether the inequality is...Ch. 3.1 - In Exercises 5-7, solve for x, 2x53Ch. 3.1 - Prob. 6ECh. 3.1 - In Exercises 5-7, solve for x,
7.
Ch. 3.1 - Which of the following results from solving x+13...
Ch. 3.1 - Prob. 9ECh. 3.1 - In Exercises 9-14, write the linear inequality in...Ch. 3.1 - In Exercises 9-14, write the linear inequality in...Ch. 3.1 - In Exercises 9-14, write the linear inequality in...Ch. 3.1 - In Exercises 9-14, write the linear inequality in...Ch. 3.1 - In Exercises 9-14, write the linear inequality in...Ch. 3.1 - In Exercises 15-22, determine whether or not the...Ch. 3.1 - In Exercises 15-22, determine whether or not the...Ch. 3.1 - In Exercises 15-22, determine whether or not the...Ch. 3.1 - In Exercises 15-22, determine whether or not the...Ch. 3.1 - In Exercises 15-22, determine whether or not the...Ch. 3.1 - In Exercises 15-22, determine whether or not the...Ch. 3.1 - Prob. 21ECh. 3.1 - Prob. 22ECh. 3.1 - In Exercises 23-26, graph the given inequality by...Ch. 3.1 - In Exercises 23-26, graph the given inequality by...Ch. 3.1 - Prob. 25ECh. 3.1 - In Exercises 23-26, graph the given inequality by...Ch. 3.1 - In Exercises 27-30, give the linear inequality...Ch. 3.1 - In Exercises 27-30, give the linear inequality...Ch. 3.1 - In Exercises 27-30, give the linear inequality...Ch. 3.1 - In Exercises 27-30, give the linear inequality...Ch. 3.1 - In Exercises 31-42, graph the given inequality....Ch. 3.1 - In Exercises 31-42, graph the given...Ch. 3.1 - In Exercises 31-42, graph the given inequality. x2Ch. 3.1 - In Exercises 31-42, graph the given inequality. x0Ch. 3.1 - In Exercises 31-42, graph the given...Ch. 3.1 - In Exercises 31-42, graph the given inequality....Ch. 3.1 - In Exercises 31-42, graph the given inequality....Ch. 3.1 - In Exercises 31-42, graph the given...Ch. 3.1 - In Exercises 31-42, graph the given inequality....Ch. 3.1 - In Exercises 31-42, graph the given...Ch. 3.1 - In Exercises 31-42, graph the given inequality....Ch. 3.1 - In Exercises 31-42, graph the given inequality....Ch. 3.1 - In Exercises 43-48, graph the feasible set for the...Ch. 3.1 - In Exercises 43-48, graph the feasible set for the...Ch. 3.1 - In Exercises 43-48, graph the feasible set for the...Ch. 3.1 - In Exercises 43-48, graph the feasible set for the...Ch. 3.1 - In Exercises 43-48, graph the feasible set for the...Ch. 3.1 - In Exercises 43-48, graph the feasible set for the...Ch. 3.1 - In Exercises 49-52, determine whether the given...Ch. 3.1 - In Exercises 49-52, determine whether the given...Ch. 3.1 - In Exercises 49-52, determine whether the given...Ch. 3.1 - In Exercises 49-52, determine whether the given...Ch. 3.1 - In Exercises 52-56, determine whether the given...Ch. 3.1 - In Exercises 52-56, determine whether the given...Ch. 3.1 - In Exercises 52-56, determine whether the given...Ch. 3.1 - In Exercises 52-56, determine whether the given...Ch. 3.1 - Give a system of inequalities for which the graph...Ch. 3.1 - The shaded region in Fig. 9 is bounded by four...Ch. 3.1 - The shaded region in Fig. 10 is bounded by four...Ch. 3.1 - Which quadrant if Fig. 11 contains no points that...Ch. 3.1 - Graph the line 4x2y=7. (a) Locate the point on the...Ch. 3.1 - 62. Graph the line
(a) Locate the point on the...Ch. 3.1 - Display the feasible set in Exercise 47.Ch. 3.1 - Display the feasible set in Exercise 48.Ch. 3.2 - 1. Determine whether the following points are in...Ch. 3.2 - A physical fitness enthusiast decides to devote...Ch. 3.2 - Prob. 1ECh. 3.2 - Prob. 2ECh. 3.2 - In Exercises 14, determine whether the given point...Ch. 3.2 - Prob. 4ECh. 3.2 - Manufacturing Consider the furniture manufacturing...Ch. 3.2 - 6. Manufacturing Consider the furniture...Ch. 3.2 - Packaging Joes Confectionary puts together two...Ch. 3.2 - Nutrition-Animal Mr. Holloway decides to feed his...Ch. 3.2 - Shipping A truck traveling from New York to...Ch. 3.2 - 10. Mining A coal company owns mines in two...Ch. 3.2 - 11. Exam Strategy A student is taking an exam...Ch. 3.2 - 12. Political Campaign—Resource Allocation A local...Ch. 3.2 - Nutrition-Dairy Cows A dairy farmer concludes that...Ch. 3.2 - Manufacturing-Resource Allocation A clothing...Ch. 3.3 - The feasible set for the nutrition problem of...Ch. 3.3 - 2. Rework the nutrition problem, assuming that...Ch. 3.3 - For each of the feasible sets in Exercises 1–4,...Ch. 3.3 - For each of the feasible sets in Exercises 14,...Ch. 3.3 - For each of the feasible sets in Exercises 14,...Ch. 3.3 - Prob. 4ECh. 3.3 - In Exercises 58, find the values of x and y that...Ch. 3.3 - In Exercises 58, find the values of x and y that...Ch. 3.3 - In Exercises 58, find the values of x and y that...Ch. 3.3 - In Exercises 5–8, find the values of x and y that...Ch. 3.3 - In Exercises 9–12, find the values of x and y that...Ch. 3.3 - In Exercises 9–12, find the values of x and y that...Ch. 3.3 - In Exercises 9–12, find the values of x and y that...Ch. 3.3 - In Exercises 9–12, find the values of x and y that...Ch. 3.3 - 13. Nutrition—People Consider the nutrition...Ch. 3.3 - 14. Nutrition—People Consider the nutrition...Ch. 3.3 - 15. Packaging Refer to Exercises 3.2, Problem 7....Ch. 3.3 - Nutrition-Animal Refer to Exercises 3.2, Problem...Ch. 3.3 - 17. Shipping Refer to Exercises 3.2, Problem 9....Ch. 3.3 - 18. Mining Refer to Exercises 3.2, Problem 10....Ch. 3.3 - Exam Strategy Refer to Exercises 3.2, Problem 11....Ch. 3.3 - Political Campaign-Resource Allocation Refer to...Ch. 3.3 - 21. Nutrition—Dairy Cows Refer to Exercises 3.2,...Ch. 3.3 - Manufacturing-Resource Allocation Refer to...Ch. 3.3 - Prob. 23ECh. 3.3 - Prob. 24ECh. 3.3 - In Exercises 25–32, find the optimal value for the...Ch. 3.3 - In Exercises 25–32, find the optimal value for the...Ch. 3.3 - In Exercises 2532, find the optimal value for the...Ch. 3.3 - In Exercises 25–32, find the optimal value for the...Ch. 3.3 - In Exercises 25–32, find the optimal value for the...Ch. 3.3 - In Exercises 25–32, find the optimal value for the...Ch. 3.3 - In Exercises 2532, find the optimal value for the...Ch. 3.3 - In Exercises 25–32, find the optimal value for the...Ch. 3.3 - 33. Manufacturing—Resource Allocation Infotron,...Ch. 3.3 - 34. Manufacturing—Production Planning An...Ch. 3.3 - Agriculture-Crop Planning A farmer has 100 acres...Ch. 3.3 - 36. Manufacturing—Resource Allocation A company...Ch. 3.3 - 37. Manufacturing The E-JEM Company produces two...Ch. 3.3 - Refining A refinery has two smelters that extract...Ch. 3.3 - 39. Nutrition—People A nutritionist, working for...Ch. 3.3 - 40. Construction—Resource Allocation A contractor...Ch. 3.3 - 41. Packaging—Product Mix The Beautiful Day Fruit...Ch. 3.3 - 42. Manufacturing—Resource Allocation The Bluejay...Ch. 3.3 - Agriculture-Crop Planning Suppose that the farmer...Ch. 3.3 - 44. Nutrition Pavan wants to add a sliced carrot...Ch. 3.3 - Packaging A small candy shop makes a special Cupid...Ch. 3.3 - Prob. 46ECh. 3.3 - 47. Packaging A bath shop sells two different gift...Ch. 3.3 - Packaging A florist offers two types of Thank You...Ch. 3.3 - Consider the following linear programming problem:...Ch. 3.3 - Consider the following linear programming problem:...Ch. 3.3 - Prob. 51ECh. 3.3 - Use Excel or Wolfram| Alpha to solve Exercise 26.Ch. 3.4 - Problems 1–3 refer to Example 1. Translate the...Ch. 3.4 - Problems 13 refer to Example 1. Translate the...Ch. 3.4 - Problems 13 refer to Example 1. Translate the...Ch. 3.4 - A linear programming problem has objective...Ch. 3.4 - 1. Figure 10(a) shows the feasible set of the...Ch. 3.4 - Figure 10(b) shows the feasible set of the...Ch. 3.4 - Consider the feasible set in Fig. 11, where three...Ch. 3.4 - Consider the feasible set in Fig. 11, where three...Ch. 3.4 - Consider the feasible set in Fig. 11, where three...Ch. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Consider the feasible set in Fig. 12, where three...Ch. 3.4 - Consider the feasible set in Fig. 12, where three...Ch. 3.4 - Consider the feasible set in Fig. 12, where three...Ch. 3.4 - Consider the feasible set in Fig. 13. For what...Ch. 3.4 - Prob. 12ECh. 3.4 - Nutrition-Animal Mr. Smith decides to feed his pet...Ch. 3.4 - Oil Production An oil company owns two refineries....Ch. 3.4 - Investment Planning Mr. Jones has $9000 to invest...Ch. 3.4 - Shipping-Product Mix A produce dealer in Florida...Ch. 3.4 - 17. Transportation—Shipping A foreign-car...Ch. 3.4 - Transportation-Shipping Consider the foreign-car...Ch. 3.4 - Manufacturing-Production Planning An oil refinery...Ch. 3.4 - 20. Manufacturing—Production Planning Suppose that...Ch. 3.4 - 21. Shipping—Resource Allocation A shipping...Ch. 3.4 - Shipping-Resource Allocation Suppose that the...Ch. 3.4 - 23. Transportation—Shipping A major coffee...Ch. 3.4 - Transportation-Shipping Consider the coffee...Ch. 3.4 - 25. Packaging—Product Mix A pet store sells three...Ch. 3.4 - Prob. 26ECh. 3.4 - 27. Refer to Fig. 6. As the lines of constant...Ch. 3.4 - Figure 16 shows the feasible set for the nutrition...Ch. 3.4 - Consider the feasible set in Fig. 17(a). In...Ch. 3.4 - Consider the feasible set in Fig. 17(a). In...Ch. 3.4 - Consider the feasible set in Fig. 17(a). In...Ch. 3.4 - Consider the feasible set in Fig. 17(a). In...Ch. 3.4 - Consider the feasible set in Fig. 17(a). In...Ch. 3.4 - Consider the feasible set in Fig. 17(a). In...Ch. 3.4 - Consider the feasible set in Fig. 17(a). In...Ch. 3.4 - Consider the feasible set in Fig. 17(a). In...Ch. 3.4 - Prob. 37ECh. 3 - State the inequality properties for addition,...Ch. 3 - What are the general forms of a linear inequality...Ch. 3 - Prob. 3FCCECh. 3 - 4. What is meant by the feasible set of a system...Ch. 3 - Prob. 5FCCECh. 3 - Prob. 6FCCECh. 3 - Prob. 7FCCECh. 3 - Prob. 8FCCECh. 3 - 9. Give a procedure for solving a linear...Ch. 3 - Prob. 1RECh. 3 - 2. Graph the linear inequality.
Ch. 3 - 3. Write the inequality whose graph is the...Ch. 3 - 4. Travel—Resource Allocation Terrapin Airlines...Ch. 3 - Nutrition-People A nutritionist is designing a new...Ch. 3 - Prob. 6RECh. 3 - Packaging-Product Mix A confectioner makes two...Ch. 3 - Prob. 8RECh. 3 - Packaging-Resource Allocation A computer company...Ch. 3 - Transportation-Shipping An appliance company has...Ch. 3 - Prob. 11RECh. 3 - Prob. 12RECh. 3 - Prob. 13RECh. 3 - Prob. 14RECh. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - When mathematicians are presented with a linear...Ch. 3 - When mathematicians are presented with a linear...Ch. 3 - When mathematicians are presented with a linear...Ch. 3 - When mathematicians are presented with a linear...Ch. 3 - When mathematicians are presented with a linear...Ch. 3 - When mathematicians are presented with a linear...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Find the general solution of the given system. 6 -(-1)x x' = -6 11 x(t) = x(t) = e5t)*[(c1 + c2(t− 1/6))(c1 + c2t)] Your answer cannoarrow_forwardYou have been hired as an intern to run analyses on the data and report the results back to Sarah; the five questions that Sarah needs you to address are given below. please do it step by step Does there appear to be a positive or negative relationship between price and screen size? Use a scatter plot to examine the relationship. Determine and interpret the correlation coefficient between the two variables. In your interpretation, discuss the direction of the relationship (positive, negative, or zero relationship). Also discuss the strength of the relationship. Estimate the relationship between screen size and price using a simple linear regression model and interpret the estimated coefficients. (In your interpretation, tell the dollar amount by which price will change for each unit of increase in screen size). Include the manufacturer dummy variable (Samsung=1, 0 otherwise) and estimate the relationship between screen size, price and manufacturer dummy as a multiple linear…arrow_forwardExercises: Find all the whole number solutions of the congruence equation. 1. 3x 8 mod 11 2. 2x+3= 8 mod 12 3. 3x+12= 7 mod 10 4. 4x+6= 5 mod 8 5. 5x+3= 8 mod 12arrow_forward
- Determine whether it's true or false and the reasoning is neededarrow_forwardIn triangle with sides of lengths a, b and c the angle a lays opposite to a. Prove the following inequality sin a 2√bc C α b a Warrow_forward1. (20 pts) Determine whether the following statements are true (T) or false (F)? (A reasoning is required.) (1) Let V be the set of all ordered pairs of real numbers. Consider the following addition and scalar multiplication operations on u = u= (u1, u2) and v = (v1, v2): u + v = (U₁ + V₁, U₂ + v₂), ku = (ku₁, u₂). Is V a vector space under the above operations? U2 (2) The set Mmxn of all m×n matrices with the usual operations of addition and scalar multiplication is a vector space. α (3) The dimension of the vector space of all matrices A = [a b] in R2×2 with a+d=0 is 4. (4) The coordinate vector of p(x) = 2-x+x² in P3 relative to the basis S = {1, 1+x, x + x2} is [4 -2 1]. (5) If a 6×4 matrix A has a rank 3, then the dimension of N(A) is 3.arrow_forward
- Scenario Sales of products by color follow a peculiar, but predictable, pattern that determines how many units will sell in any given year. This pattern is shown below Product Color 1995 1996 1997 Red 28 42 21 1998 23 1999 29 2000 2001 2002 Unit Sales 2003 2004 15 8 4 2 1 2005 2006 discontinued Green 26 39 20 22 28 14 7 4 2 White 43 65 33 36 45 23 12 Brown 58 87 44 48 60 Yellow 37 56 28 31 Black 28 42 21 Orange 19 29 Purple Total 28 42 21 49 68 78 95 123 176 181 164 127 24 179 Questions A) Which color will sell the most units in 2007? B) Which color will sell the most units combined in the 2007 to 2009 period? Please show all your analysis, leave formulas in cells, and specify any assumptions you make.arrow_forward5. (20%) The linear transformation L: P3 → P2 defined by L(f(x)) = f'(x)+ f(0). (a) Find the representing matrix A of L with respect to the ordered basis {x2, x, 1} for P3, and the ordered basis {2,1 - x} for P2. (b) Find the coordinates of the f(x) = 2x² +2 in P3 with respect to the ordered basis {x2,-x, 1}, and find the coordinates of L(f(x)) with respect to the ordered basis {2,1-x}arrow_forwardOne hundred students were surveyed about their preference between dogs and cats. The following two-way table displays data for the sample of students who responded to the survey. Preference Male Female TOTAL Prefers dogs \[36\] \[20\] \[56\] Prefers cats \[10\] \[26\] \[36\] No preference \[2\] \[6\] \[8\] TOTAL \[48\] \[52\] \[100\] problem 1 Find the probability that a randomly selected student prefers dogs.Enter your answer as a fraction or decimal. \[P\left(\text{prefers dogs}\right)=\] Incorrect Check Hide explanation Preference Male Female TOTAL Prefers dogs \[\blueD{36}\] \[\blueD{20}\] \[\blueE{56}\] Prefers cats \[10\] \[26\] \[36\] No preference \[2\] \[6\] \[8\] TOTAL \[48\] \[52\] \[100\] There were \[\blueE{56}\] students in the sample who preferred dogs out of \[100\] total students.arrow_forward
- For the spinner below, assume that the pointer can never lie on a borderline. Find the following probabilities. (enter the probabilities as fractions)arrow_forwardEvaluate the following integrals as they are writtenarrow_forwardFind the values of x, y, and z. Round to the nearest tenth, if necessary. 8, 23arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning

College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning

Algebra for College Students
Algebra
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning

College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Solve ANY Optimization Problem in 5 Steps w/ Examples. What are they and How do you solve them?; Author: Ace Tutors;https://www.youtube.com/watch?v=BfOSKc_sncg;License: Standard YouTube License, CC-BY
Types of solution in LPP|Basic|Multiple solution|Unbounded|Infeasible|GTU|Special case of LP problem; Author: Mechanical Engineering Management;https://www.youtube.com/watch?v=F-D2WICq8Sk;License: Standard YouTube License, CC-BY
Optimization Problems in Calculus; Author: Professor Dave Explains;https://www.youtube.com/watch?v=q1U6AmIa_uQ;License: Standard YouTube License, CC-BY
Introduction to Optimization; Author: Math with Dr. Claire;https://www.youtube.com/watch?v=YLzgYm2tN8E;License: Standard YouTube License, CC-BY