A First Course in Differential Equations with Modeling Applications (MindTap Course List)
11th Edition
ISBN: 9781305965720
Author: Dennis G. Zill
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 3.2, Problem 4E
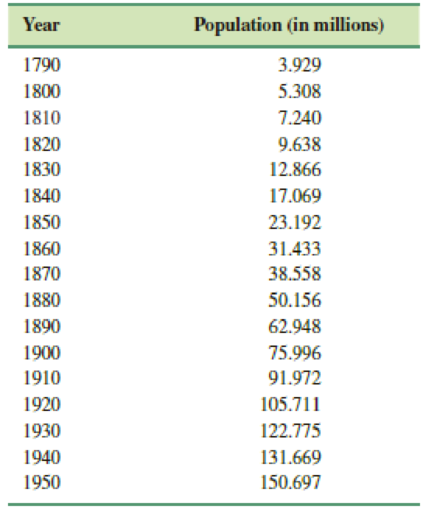
- (a) Census data for the United States between 1790 and 1950 are given in Table 3.2.1. Construct a logistic population model using the data from 1790, 1850, and 1910.
- (b) Construct a table comparing actual census population with the population predicted by the model in part (a). Compute the error and the percentage error for each entry pair.
TABLE 3.2.1
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
5. If g'(5) 10 and h'(5)=-4, find f'(5) for f(x)=4g(x)-2h(x)+3.
2. Find each derivative. Write answers with positive exponents.
a)
Dx 9x
-3
[97]
b) f'(3) if f(x) = x²-5x²
8
T3.2: Prove that if the Graceful Tree Conjecture (every tree has a graceful labeling) is true and T' is
a tree with m edges, then K2, decomposes into 2m - 1 copies of T.
Hint - Delete a leaf to get 7" and apply the decomposition of K2(m-1)+1 = K2m-1 into T'. Then
explain how the decomposition allows the pendant edge to be added to a new vertex to obtain a
decomposition of K2m into copies of T.
Chapter 3 Solutions
A First Course in Differential Equations with Modeling Applications (MindTap Course List)
Ch. 3.1 - The population of a community is known to increase...Ch. 3.1 - Suppose it is known that the population of the...Ch. 3.1 - The population of a town grows at a rate...Ch. 3.1 - The population of bacteria in a culture grows at a...Ch. 3.1 - The radioactive isotope of lead, Pb-209, decays at...Ch. 3.1 - Initially 100 milligrams of a radioactive...Ch. 3.1 - Determine the half-life of the radioactive...Ch. 3.1 - Consider the initial-value problem dA/dt = kA,...Ch. 3.1 - When a vertical beam of light passes through a...Ch. 3.1 - When interest is compounded continuously, the...
Ch. 3.1 - Carbon Dating Archaeologists used pieces of burned...Ch. 3.1 - The Shroud of Turin, which shows the negative...Ch. 3.1 - Newtons Law of Cooling/Warming A thermometer is...Ch. 3.1 - A thermometer is taken from an inside room to the...Ch. 3.1 - A small metal bar, whose initial temperature was...Ch. 3.1 - Two large containers A and B of the same size are...Ch. 3.1 - A thermometer reading 70 F is placed in an oven...Ch. 3.1 - At t = 0 a sealed test tube containing a chemical...Ch. 3.1 - A dead body was found within a closed room of a...Ch. 3.1 - The rate at which a body cools also depends on its...Ch. 3.1 - A tank contains 200 liters of fluid in which 30...Ch. 3.1 - Solve Problem 21 assuming that pure water is...Ch. 3.1 - A large tank is filled to capacity with 500...Ch. 3.1 - In Problem 23, what is the concentration c(t) of...Ch. 3.1 - Solve Problem 23 under the assumption that the...Ch. 3.1 - Determine the amount of salt in the tank at time t...Ch. 3.1 - A large tank is partially filled with 100 gallons...Ch. 3.1 - In Example 5 the size of the tank containing the...Ch. 3.1 - A 30-volt electromotive force is applied to an...Ch. 3.1 - Prob. 30ECh. 3.1 - A 100-volt electromotive force is applied to an...Ch. 3.1 - A 200-volt electromotive force is applied to an...Ch. 3.1 - An electromotive force E(t)={120,0t200,t20 is...Ch. 3.1 - An LR-series circuit has a variable inductor with...Ch. 3.1 - Air Resistance In (14) of Section 1.3 we saw that...Ch. 3.1 - How High?No Air Resistance Suppose a small...Ch. 3.1 - How High?Linear Air Resistance Repeat Problem 36,...Ch. 3.1 - Skydiving A skydiver weighs 125 pounds, and her...Ch. 3.1 - Rocket Motion Suppose a small single-stage rocket...Ch. 3.1 - Rocket MotionContinued In Problem 39 suppose of...Ch. 3.1 - Evaporating Raindrop As a raindrop falls, it...Ch. 3.1 - Prob. 42ECh. 3.1 - Prob. 43ECh. 3.1 - Constant-Harvest model A model that describes the...Ch. 3.1 - Drug Dissemination A mathematical model for the...Ch. 3.1 - Memorization When forgetfulness is taken into...Ch. 3.1 - Heart Pacemaker A heart pacemaker, shown in Figure...Ch. 3.1 - Sliding Box (a) A box of mass m slides down an...Ch. 3.1 - Sliding Box—Continued
In Problem 48 let s(t) be...Ch. 3.1 - What Goes Up (a) It is well known that the model...Ch. 3.2 - The number N(t) of supermarkets throughout the...Ch. 3.2 - The number N(t) of people in a community who are...Ch. 3.2 - A model for the population P(t) in a suburb of a...Ch. 3.2 - Census data for the United States between 1790 and...Ch. 3.2 - (a) If a constant number h of fish are harvested...Ch. 3.2 - Investigate the harvesting model in Problem 5 both...Ch. 3.2 - Repeat Problem 6 in the case a = 5, b = 1, h = 7.Ch. 3.2 - (a) Suppose a = b = 1 in the Gompertz differential...Ch. 3.2 - Two chemicals A and B are combined to form a...Ch. 3.2 - Solve Problem 9 if 100 grams of chemical A is...Ch. 3.2 - Leaking cylindrical tank A tank in the form of a...Ch. 3.2 - Leaking cylindrical tank—continued When friction...Ch. 3.2 - Leaking Conical Tank A tank in the form of a...Ch. 3.2 - Inverted Conical Tank Suppose that the conical...Ch. 3.2 - Air Resistance A differential equation for the...Ch. 3.2 - How High?Nonlinear Air Resistance Consider the...Ch. 3.2 - That Sinking Feeling (a) Determine a differential...Ch. 3.2 - Solar Collector The differential equation...Ch. 3.2 - Tsunami (a) A simple model for the shape of a...Ch. 3.2 - Evaporation An outdoor decorative pond in the...Ch. 3.2 - Doomsday equation Consider the differential...Ch. 3.2 - Doomsday or extinction Suppose the population...Ch. 3.2 - Skydiving A skydiver is equipped with a stopwatch...Ch. 3.2 - Prob. 27ECh. 3.2 - Old Man River In Figure 3.2.8(a) suppose that the...Ch. 3.2 - Prob. 29ECh. 3.2 - Prob. 30ECh. 3.2 - Prob. 31ECh. 3.2 - Prob. 32ECh. 3.2 - Time Drips By The clepsydra, or water clock, was a...Ch. 3.2 - (a) Suppose that a glass tank has the shape of a...Ch. 3.2 - Prob. 35ECh. 3.3 - We have not discussed methods by which systems of...Ch. 3.3 - In Problem 1 suppose that time is measured in...Ch. 3.3 - Use the graphs in Problem 2 to approximate the...Ch. 3.3 - Construct a mathematical model for a radioactive...Ch. 3.3 - Potassium-40 Decay The chemical element potassium...Ch. 3.3 - Potassium-Argon Dating The knowledge of how K-40...Ch. 3.3 - Consider two tanks A and B, with liquid being...Ch. 3.3 - Use the information given in Figure 3.3.6 to...Ch. 3.3 - Two very large tanks A and B are each partially...Ch. 3.3 - Three large tanks contain brine, as shown in...Ch. 3.3 - Consider the Lotka-Volterra predator-prey model...Ch. 3.3 - Show that a system of differential equations that...Ch. 3.3 - Determine a system of first-order differential...Ch. 3.3 - Prob. 16ECh. 3.3 - SIR Model A communicable disease is spread...Ch. 3.3 - Prob. 18ECh. 3.3 - Prob. 19ECh. 3.3 - Prob. 20ECh. 3.3 - Mixtures Solely on the basis of the physical...Ch. 3.3 - Newtons Law of Cooling/Warming As shown in Figure...Ch. 3 - Answer Problems 1 and 2 without referring back to...Ch. 3 - Answer Problems 1 and 2 without referring back to...Ch. 3 - Prob. 3RECh. 3 - Air containing 0.06% carbon dioxide is pumped into...Ch. 3 - tzi the Iceman In September of 1991 two German...Ch. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Suppose a cell is suspended in a solution...Ch. 3 - Suppose that as a body cools, the temperature of...Ch. 3 - According to Stefans law of radiation the absolute...Ch. 3 - Suppose an RC-series circuit has a variable...Ch. 3 - A classical problem in the calculus of variations...Ch. 3 - A model for the populations of two interacting...Ch. 3 - Initially, two large tanks A and B each hold 100...Ch. 3 - Prob. 15RECh. 3 - When all the curves in a family G(x, y, c1) = 0...Ch. 3 - Prob. 17RECh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Sawing Wood A long uniform piece of wood (cross...Ch. 3 - Solve the initial-value problem in Problem 20 when...Ch. 3 - Prob. 22RE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Use the matrix tree theorem to determine the number of spanning trees of the graphs Kr∨sK1.These are the graphs formed by by adding all edges between a complete graph on r vertices and atrivial graph (no edges) on s vertices.arrow_forwardThe maximum capacity spanning tree problem is as follows for a given graph G = (V, E) withcapacities c(uv) on the edges. The capacity of a tree T is defined as the minimum capacity of anedge in T. The maximum capacity spanning tree problem is to determine the maximum capacity ofa spanning tree.(i) Describe how to modify the input graph to find a maximum weight spanning tree making use ofa minimum weight spanning tree algorithm.(ii) Show that a maximum (weight) spanning tree is also a maximum capacity spanning tree.(iii) Is the converse of part (ii) true? That is, is it true that a maximum capacity spanning tree is alsoa maximum spanning tree? Either give counterexamples (of all sizes) or a proof.(iv) Prove the following max-min result. The maximum capacity of a spanning tree is equal to theminimum bottleneck value of a cut. For a subset U ⊆ V , the cut [U, V − U] is the set of edgesbetween U and V − U. The bottleneck value of a cut [U, V − U] is the largest capacity among theedges of…arrow_forward1) Find The inverse The domain of m(x) = tion and of the function The inverse function 3- √x-aarrow_forward
- Prove that the following version of a greedy algorithm produces a minimum spanning tree in aweighted graph. Start with a vertex v as the initial tree and at each stage add an edge with minimumweight having exactly one end in the current tree. Stop when all vertices have been addedarrow_forwardb. According to the analyst, what is the probability that the confidence score is not 1? 11. Professor Sanchez has been teaching Principles of Economics for over 25 years. He uses the following scale for grading. Grade Numerical Score Probability A 4 0.10 B 3 0.30 C 2 0.40 D 1 0.10 F O 0.10 a. Depict the probability distribution graphically. Comment on whether or not the probability distribution is symmetric. b. Convert the probability distribution to a cumulative probability distribution. C. What is the probability of earning at least a B in Professor Sanchez's course? d. What is the probability of passing Professor Sanchez's course? 2. Professor Khurana expects to be able to use her grant money to fund up to two students for research assistance. While she realizes that there is a 5% chance that she may not be able to fund any student, there is an 80% chance that she will be able to fund two students. a. What hat is the proarrow_forwardGraph the following function. Please also graph the asymptote. Thank you.arrow_forward
- A ladder 27 feet long leans against a wall and the foot of the ladder is sliding away at a constant rate of 3 feet/sec. Meanwhile, a firefighter is climbing up the ladder at a rate of 2 feet/sec. When the firefighter has climbed up 6 feet of the ladder, the ladder makes an angle of л/3 with the ground. Answer the two related rates questions below. (Hint: Use two carefully labeled similar right triangles.) (a) If h is the height of the firefighter above the ground, at the instant the angle of the ladder with the ground is л/3, find dh/dt= feet/sec. (b) If w is the horizontal distance from the firefighter to the wall, at the instant the angle of the ladder with the ground is л/3, find dw/dt= feet/sec.arrow_forwardTwo cars start moving from the same point. One travels south at 60 mi/h and the other travels west at 25 mi/h. At what rate (in mi/h) is the distance between the cars increasing four hours later? Step 1 Using the diagram of a right triangle given below, the relation between x, y, and z is z² = x²+ +12 x Step 2 We must find dz/dt. Differentiating both sides and simplifying gives us the following. 2z dz dt dx 2x. +2y dt dx dy dz x +y dt dt dt 2z dy dt × dx (x+y dt dy dtarrow_forwardAn elastic rope is attached to the ground at the positions shown in the picture. The rope is being pulled up along the dotted line. Assume the units are meters. 9 ground level Assume that x is increasing at a rate of 3 meters/sec. (a) Write as a function of x: 0= (b) When x=10, the angle is changing at a rate of rad/sec. (c) Let L be the the left hand piece of rope and R the right hand piece of rope. When x=10, is the rate of change of L larger than the rate of change of R? ○ Yes ○ Noarrow_forward
- At a local college, for sections of economics are taught during the day and two sections are taught at night. 70 percent of the day sections are taught by full time faculty. 20 percent of the evening sections are taught by full time faculty. If Jane has a part time teacher for her economics course, what is the probability that she is taking a night class?arrow_forward4.1 Basic Rules of Differentiation. 1. Find the derivative of each function. Write answers with positive exponents. Label your derivatives with appropriate derivative notation. a) y=8x-5x3 4 X b) y=-50 √x+11x -5 c) p(x)=-10x²+6x3³arrow_forwardNo chatgpt pls will upvotearrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
Sampling Methods and Bias with Surveys: Crash Course Statistics #10; Author: CrashCourse;https://www.youtube.com/watch?v=Rf-fIpB4D50;License: Standard YouTube License, CC-BY
Statistics: Sampling Methods; Author: Mathispower4u;https://www.youtube.com/watch?v=s6ApdTvgvOs;License: Standard YouTube License, CC-BY