Chapter 3.2, Problem 45E

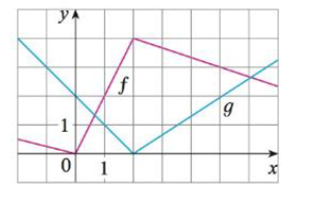
If f and g are the functions whose graphs are shown, let u(x) = f(x)g(x) and v(x) = f(x)/g(x).

(a) Find u'(l).

(b) Find v'(5).

To determine

To find: The derivative of $u\left(x\right)$ at $x=1$.

Answer to Problem 45E

The derivative of $u\left(x\right)$ at $x=1$ is $u^{\prime }\left(1\right)=0$.

Explanation of Solution

Given:

The function is $u\left(x\right)=f\left(x\right)g\left(x\right)$.

Derivative rule:

Product Rule: $\frac{d}{dx}\left[f_1\left(x\right)f_2\left(x\right)\right]=f_1\left(x\right)\frac{d}{dx}\left[f_2\left(x\right)\right]+f_2\left(x\right)\frac{d}{dx}\left[f_1\left(x\right)\right]$

Calculation:

Obtain the value of $u^{\prime }\left(1\right)$.

$u^{\prime }\left(x\right)=\frac{d}{dx}\left(f\left(x\right)g\left(x\right)\right)$

Apply the product rule (1) and simplify the terms,

$\begin{array}{c}{u}^{\prime }\left(x\right)=f\left(x\right)\frac{d}{dx}\left(g\left(x\right)\right)+g\left(x\right)\frac{d}{dx}\left(f\left(x\right)\right)\\ =f\left(x\right)g^{\prime }\left(x\right)+g\left(x\right)f^{\prime }\left(x\right)\end{array}$

Substitute 1 for x in $u^{\prime }\left(x\right)$,

$u^{\prime }\left(1\right)=f\left(1\right)g^{\prime }\left(1\right)+g\left(1\right)f^{\prime }\left(1\right)$ (1)

From the given graph, it is observed that $f\left(1\right)=2\text{ , }g\left(1\right)=1$ , the function $f\left(x\right)$ is linear from $\left(0,0\right)$ to $\left(2,4\right)$ and the function $g\left(x\right)$ is linear that passes through the points $\left(0,2\right)\text{ and }\left(2,0\right)$.

Obtain the values $f^{\prime }\left(1\right)\text{ and }{g}^{\prime }\left(1\right)$.

Since the slope of the line at every point is equal, the slope of the function $f\left(x\right)$ passes through the points $\left(0,0\right)\text{ and }\left(2,4\right)$ is,

$\begin{array}{c}{m}_1=\frac{4-0}{2-0}\\ =2\end{array}$

Therefore, the value of $f^{\prime }\left(1\right)=2$.

The slope of the function $g\left(x\right)$ passing through the points $\left(0,2\right)\text{ and }\left(2,0\right)$ is,

$\begin{array}{c}{m}_2=\frac{0-2}{2-0}\\ =-1\end{array}$

Therefore, the value of $g^{\prime }\left(1\right)=-1$.

Substitute the values $f\left(1\right)=2,g\left(1\right)=1,f^{\prime }\left(1\right)\text{=2 and }{g}^{\prime }\left(1\right)=-1$ in equation (1),

$\begin{array}{c}{u}^{\prime }\left(1\right)=\left(2\times -1\right)+\left(1\times 2\right)\\ =-2+2\\ =0\end{array}$

Therefore, the derivative of $u\left(x\right)$ at $x=1$ is $u^{\prime }\left(1\right)=0$.

To determine

To find: The derivative of $v\left(x\right)$ at $x=5$.

Answer to Problem 45E

The derivative of $v\left(x\right)$ at $x=5$ is $v^{\prime }\left(5\right)=\frac{-2}{3}$.

Explanation of Solution

Given:

The function is $v\left(x\right)=\frac{f\left(x\right)}{g\left(x\right)}$.

Derivative rule:

Quotient Rule: If $f_1\left(x\right)$ and $f_2\left(x\right)$ are both differentiable, then

$\frac{d}{dx}\left[\frac{f_1\left(x\right)}{f_2\left(x\right)}\right]=\frac{f_2\left(x\right)\frac{d}{dx}\left[f_1\left(x\right)\right]-f_1\left(x\right)\frac{d}{dx}\left[f_2\left(x\right)\right]}{{\left[f_{2}x\right]}^2}$

Calculation:

Obtain the value of $v^{\prime }\left(5\right)$.

$v^{\prime }\left(x\right)=\frac{d}{dx}\left(\frac{f\left(x\right)}{g\left(x\right)}\right)$

Apply the Quotient rule (1) and simplify the terms,

$\begin{array}{c}{v}^{\prime }\left(x\right)=\frac{g\left(x\right)\frac{d}{dx}\left(f\left(x\right)\right)-f\left(x\right)\frac{d}{dx}\left(g\left(x\right)\right)}{{\left(g\left(x\right)\right)}^2}\\ =\frac{g\left(x\right)f^{\prime }\left(x\right)-f\left(x\right)g^{\prime }\left(x\right)}{{\left(g\left(x\right)\right)}^2}\end{array}$

Substitute 5 for x in $v^{\prime }\left(x\right)$,

$v^{\prime }\left(5\right)=\frac{g\left(5\right)f^{\prime }\left(5\right)-f\left(5\right)g^{\prime }\left(5\right)}{{\left(g\left(5\right)\right)}^2}$ (2)

From the given graph, it is observed that $f\left(5\right)=3\text{ , }g\left(5\right)=2$, the function $f\left(x\right)$ is linear that passes through the points $\left(2,4\right)\text{ and }\left(5,3\right)$ and the function $g\left(x\right)$ is linear that passes through the points $\left(2,0\right)\text{ and }\left(5,2\right)$.

Obtain the values $f^{\prime }\left(5\right)\text{ and }{g}^{\prime }\left(5\right)$.

Since the slope of the line at every point is equal, the slope of the function $f\left(x\right)$ passes through the points $\left(2,4\right)\text{ and }\left(5,3\right)$ is,

$\begin{array}{c}{m}_3=\frac{3-4}{5-2}\\ =\frac{-1}{3}\end{array}$

Therefore, the value of $f^{\prime }\left(5\right)=-\frac{1}{3}$.

The slope of the function $g\left(x\right)$ passing through the points $\left(2,0\right)\text{ and }\left(5,2\right)$ is,

$\begin{array}{c}{m}_3=\frac{2-0}{5-2}\\ =\frac{2}{3}\end{array}$

Therefore, the value of $g^{\prime }\left(5\right)=\frac{2}{3}$.

Substitute the values $f\left(5\right)=3\text{ , }g\left(5\right)=2,f^{\prime }\left(5\right)\text{=}\frac{-1}{3}\text{ and }{g}^{\prime }\left(5\right)=\frac{2}{3}$ in equation (2),

$\begin{array}{c}{v}^{\prime }\left(5\right)=\frac{\left(2\times \frac{-1}{3}\right)-\left(3\times \frac{2}{3}\right)}{2^2}\\ =\frac{-\frac{2}{3}-\frac{6}{3}}{2^2}\\ =\frac{-8}{3\times 4}\\ =\frac{-2}{3}\end{array}$

Therefore, the derivative of $v\left(x\right)$ at $x=5$ is $v^{\prime }\left(5\right)=\frac{-2}{3}$.