Chapter 3, Problem 68RE

(a)

To determine

To find: The velocity and the acceleration function.

Explanation of Solution

Given: The expression coordinate of particle is $y=t^3-12t+3$

Velocity is the derivation of the first position.

So, the expression for velocity is calculated as:

  $\begin{array}{c}v=y^{\prime }\\ =3t^2-12\end{array}$

Acceleration is the second derivative of position. So,

  $\begin{array}{c}a=y^{″}\\ =6t\end{array}$

Therefore, the velocity function is $v=3t^2-12$ and the acceleration function is $a=6t$ .

(b)

To determine

To find: When the particle is moving upward and when it is moving downward.

Explanation of Solution

Given: The expression coordinate of particle is $y=t^3-12t+3$

Velocity is the derivation of the first position.

So, the expression for velocity is calculated as:

  $\begin{array}{c}v=y^{\prime }\\ =3t^2-12\end{array}$

Equate the above equation to zero.

  $\begin{array}{c}0=3t^2-12\\ t=2\end{array}$

Plugging in the values lesser and greater than $2$ it is obtained that $t$ value less than $2$ decreases. So, the particle is moving downward during this time and likewise the particle is moving up for the rest of the time.

Therefore, the particle is moving downward from the time $\left[0,2\right)$ and moving upward from time $\left(2,\infty \right)$ .

(c)

To determine

To find: The distance that the particle travels in the time interval.

Explanation of Solution

Given: The expression coordinate of particle is $y=t^3-12t+3$

Velocity is the derivation of the first position.

So, the expression for velocity is calculated as:

  $\begin{array}{c}v=y^{\prime }\\ =3t^2-12\end{array}$

Equate the above equation to zero.

  $\begin{array}{c}0=3t^2-12\\ t=\pm 2\end{array}$

To find the total distance, break up the position function into two intervals $0\le t\le 2$ and $2<t\le 3$ .

  $\begin{array}{c}y\left(0\right)=3\\ y\left(2\right)=-13\\ y\left(3\right)=-6\end{array}$

Hence,

  $\begin{array}{c}\text{Total}\text{distanc}=\left|y\left(0\right)-y\left(2\right)\right|+\left|y\left(2\right)-y\left(3\right)\right|\\ =23\end{array}$

(d)

To determine

To graph : The position, velocity and the acceleration function.

Explanation of Solution

Given: The expression coordinate of particle is $y=t^3-12t+3$

The graph of position, velocity and the acceleration function on a single plane is shown in figure below.

  

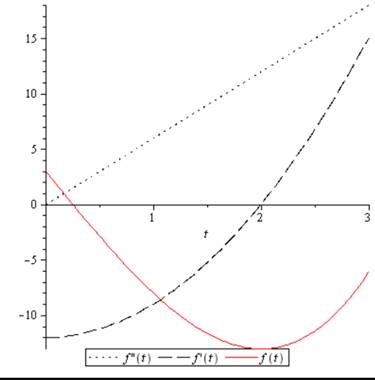
Figure (1)

Therefore, the graph of position, velocity and the acceleration function on a single plane is shown in Figure (1).

(e)

To determine

To graph : When the particle is speeding up and speeding down..

Explanation of Solution

Given: The expression coordinate of particle is $y=t^3-12t+3$

The graph of position, velocity and the acceleration function on a single plane is shown in figure below.

  

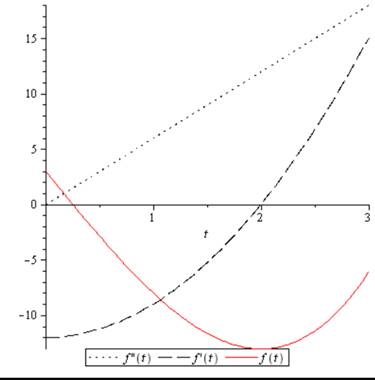
Figure (1)

From the graph both the acceleration and velocity have the same sign after $x>2$ .

Hence, the particle is speeding up during $t\in \left(2,3\right)$