Chapter 3.2, Problem 39E

Time to review: The following table presents the time taken to review articles that were submitted for publication to the journal Technometrics during a recent year. A few articles took longer than 9 months to review; these are omitted from the table. Consider the data to be a population.

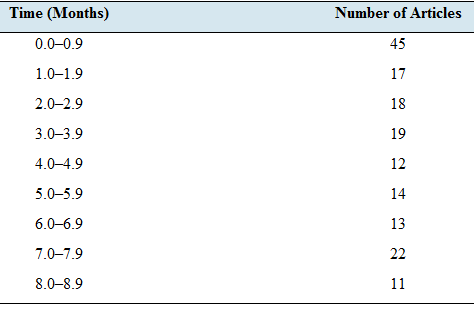
1. Approximate the variance of the times.
2. Approximate the standard deviation of the times.

To determine

To find the Population variance for given data.

Answer to Problem 39E

Variance = 0.384

Explanation of Solution

Given:

The data

Time (Months)	Number of Articles
0.0−0.9	45
1.0−1.9	17
2.0−2.9	18
3.0−3.9	19
4.0−4.9	12
5.0−5.9	14
6.0−6.9	13
7.0−7.9	22
8.0−8.9	11

Calculation:

Time (Months)	Number of Articles(fi)	Mid Value(xi)	$f_i{x}_i$	$f_i{\left(x_i-\overline{x}\right)}^2$
0.0−0.9	45	0.5	22.5	10.27
1.0−1.9	17	1.5	25.5	4.86
2.0−2.9	18	2.5	45	1.45
3.0−3.9	19	3.5	66.5	0.04
4.0−4.9	12	4.5	54	0.63
5.0−5.9	14	5.5	77	3.22
6.0−6.9	13	6.5	84.5	7.81
7.0−7.9	22	7.5	165	14.40
8.0−8.9	11	8.5	93.5	23.00
Sum	171		633.50	65.69
Mean	3.70

  $\begin{array}{c}\text{Mean = }\frac{\sum x_i}{n}\\ =\frac{633.50}{171}\\ =3.70\end{array}$

  $\begin{array}{c}\text{Variance = }\frac{\sum f_i{\left(x_i-\overline{x}\right)}^2}{n}\\ =\frac{65.69}{171}\\ =0.384\end{array}$

The variance for the given data is 0.384.

To determine

To find the Population standard deviation for given data.

Answer to Problem 39E

Standard deviation = 0.62

Explanation of Solution

Calculation:

Time (Months)	Number of Articles(fi)	Mid Value(xi)	$f_i{x}_i$	$f_i{\left(x_i-\overline{x}\right)}^2$
0.0−0.9	45	0.5	22.5	10.27
1.0−1.9	17	1.5	25.5	4.86
2.0−2.9	18	2.5	45	1.45
3.0−3.9	19	3.5	66.5	0.04
4.0−4.9	12	4.5	54	0.63
5.0−5.9	14	5.5	77	3.22
6.0−6.9	13	6.5	84.5	7.81
7.0−7.9	22	7.5	165	14.40
8.0−8.9	11	8.5	93.5	23.00
Sum	171		633.50	65.69
Mean	3.70

  $\begin{array}{c}\text{Standard Deviation = }\sqrt{\frac{\sum f_i{\left(x_i-\overline{x}\right)}^2}{n}}\\ =\sqrt{\frac{65.69}{171}}\\ =0.62\end{array}$

The Standard deviation for the given data is 0.62.