
(a)
Write an inequality that relates the number of empty boxes the boosters need to buy for the next game, the number of empty boxes on hand, and the maximum number of boxes of popcorn the boosters expect to sell.
(a)
Answer to Problem 1MP
Explanation of Solution
Given :
The boosters have 40 empty boxes on hand from the last game and will need to buy more for the next game. They know from previous experience that they can expect to sell no more than 310 boxes at each game.
Calculation:
The boosters have 40 empty boxes on hand from the last game.
Let
the number of empty boxes the boosters need to buy for the next game = x
So, the total number of empty boxes the boosters have in hand = x + 40
The maximum number of boxes the boosters can sell in each game is 310.
Hence , x + 40 should not exceed 310.
So, the inequality that relates the number of empty boxes the boosters need to buy for the next game, the number of empty boxes on hand, and the maximum number of boxes of popcorn the boosters expect to sell :
(b)
Solve your inequality from part (a).
(b)
Answer to Problem 1MP
Explanation of Solution
Given :
The boosters have 40 empty boxes on hand from the last game and will need to buy more for the next game. They know from previous experience that they can expect to sell no more than 310 boxes at each game.
Calculation:
From part (a) , the inequality that relates the number of empty boxes x the boosters need to buy for the next game, the number of empty boxes on hand, and the maximum number of boxes of popcorn the boosters expect to sell :
Solve the inequality :
So, the number of empty boxes the boosters need to buy for the next game should not exceed 270.
(c)
Find the packages of empty boxes that the athletic boosters can buy in order to have enough for the next game. (Consider that they might buy more than one package of empty boxes. Also note that once the boosters have enough empty boxes, they do not need to buy any additional packages.)
(c)
Answer to Problem 1MP
- 4 packages of 75 empty boxes per package.
- 1 package of 200 empty boxes per package and 1 package of 75 empty boxes per package.
Explanation of Solution
Given :
Empty boxes are sold in various quantities, as shown in the table below.
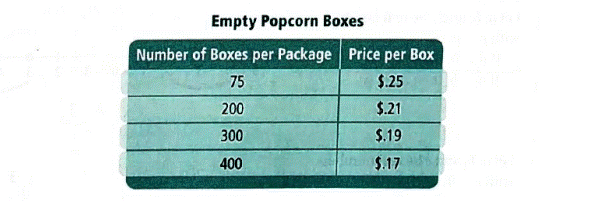
Calculation:
From part (b) , the number of empty boxes the boosters need to buy for the next game should not exceed 270.
So, they cannot buy the package that has 300 and 400 boxes, since it will exceed the required number of boxes and money spent will be excessive.
They can buy packages with 75 and 200 boxes per package in combination :
- 4 packages of 75 empty boxes per package.
- 1 package of 200 empty boxes per package and 1 package of 75 empty boxes per package.
Chapter 3 Solutions
High School Math 2015 Common Core Algebra 1 Student Edition Grade 8/9
Additional Math Textbook Solutions
Elementary Statistics (13th Edition)
Introductory Statistics
Algebra and Trigonometry (6th Edition)
College Algebra with Modeling & Visualization (5th Edition)
University Calculus: Early Transcendentals (4th Edition)
Elementary Statistics: Picturing the World (7th Edition)
- Compare the interest earned from #1 (where simple interest was used) to #5 (where compound interest was used). The principal, annual interest rate, and time were all the same; the only difference was that for #5, interest was compounded quarterly. Does the difference in interest earned make sense? Select one of the following statements. a. No, because more money should have been earned through simple interest than compound interest. b. Yes, because more money was earned through simple interest. For simple interest you earn interest on interest, not just on the amount of principal. c. No, because more money was earned through simple interest. For simple interest you earn interest on interest, not just on the amount of principal. d. Yes, because more money was earned when compounded quarterly. For compound interest you earn interest on interest, not just on the amount of principal.arrow_forwardCompare and contrast the simple and compound interest formulas. Which one of the following statements is correct? a. Simple interest and compound interest formulas both yield principal plus interest, so you must subtract the principal to get the amount of interest. b. Simple interest formula yields principal plus interest, so you must subtract the principal to get the amount of interest; Compound interest formula yields only interest, which you must add to the principal to get the final amount. c. Simple interest formula yields only interest, which you must add to the principal to get the final amount; Compound interest formula yields principal plus interest, so you must subtract the principal to get the amount of interest. d. Simple interest and compound interest formulas both yield only interest, which you must add to the principal to get the final amount.arrow_forwardSara would like to go on a vacation in 5 years and she expects her total costs to be $3000. If she invests $2500 into a savings account for those 5 years at 8% interest, compounding semi-annually, how much money will she have? Round your answer to the nearest cent. Show you work. Will she be able to go on vacation? Why or why not?arrow_forward
- If $8000 is deposited into an account earning simple interest at an annual interest rate of 4% for 10 years, howmuch interest was earned? Show you work.arrow_forward10-2 Let A = 02-4 and b = 4 Denote the columns of A by a₁, a2, a3, and let W = Span {a1, a2, a̸3}. -4 6 5 - 35 a. Is b in {a1, a2, a3}? How many vectors are in {a₁, a₂, a3}? b. Is b in W? How many vectors are in W? c. Show that a2 is in W. [Hint: Row operations are unnecessary.] a. Is b in {a₁, a2, a3}? Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. ○ A. No, b is not in {a₁, a2, 3} since it cannot be generated by a linear combination of a₁, a2, and a3. B. No, b is not in (a1, a2, a3} since b is not equal to a₁, a2, or a3. C. Yes, b is in (a1, a2, a3} since b = a (Type a whole number.) D. Yes, b is in (a1, a2, 3} since, although b is not equal to a₁, a2, or a3, it can be expressed as a linear combination of them. In particular, b = + + ☐ az. (Simplify your answers.)arrow_forward14 14 4. The graph shows the printing rate of Printer A. Printer B can print at a rate of 25 pages per minute. How does the printing rate for Printer B compare to the printing rate for Printer A? The printing rate for Printer B is than the rate for Printer A because the rate of 25 pages per minute is than the rate of for Printer A. pages per minute RIJOUT 40 fy Printer Rat Number of Pages 8N WA 10 30 20 Printer A 0 0 246 Time (min) Xarrow_forward
- OR 16 f(x) = Ef 16 χ по x²-2 410 | y = (x+2) + 4 Y-INT: y = 0 X-INT: X=0 VA: x=2 OA: y=x+2 0 X-INT: X=-2 X-INT: y = 2 VA 0 2 whole. 2-2 4 y - (x+2) = 27-270 + xxx> 2 क् above OA (x+2) OA x-2/x²+0x+0 2 x-2x 2x+O 2x-4 4 X<-1000 4/4/2<0 below Of y VA X=2 X-2 OA y=x+2 -2 2 (0,0) 2 χarrow_forwardI need help solving the equation 3x+5=8arrow_forwardWhat is the domain, range, increasing intervals (theres 3), decreasing intervals, roots, y-intercepts, end behavior (approaches four times), leading coffiencent status (is it negative, positivie?) the degress status (zero, undifined etc ), the absolute max, is there a absolute minimum, relative minimum, relative maximum, the root is that has a multiplicity of 2, the multiplicity of 3.arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





