
Concept explainers
(a)
Show the direction
(a)
Explanation of Solution
Show the direction vector in the FCC unit cell for the cubic direction
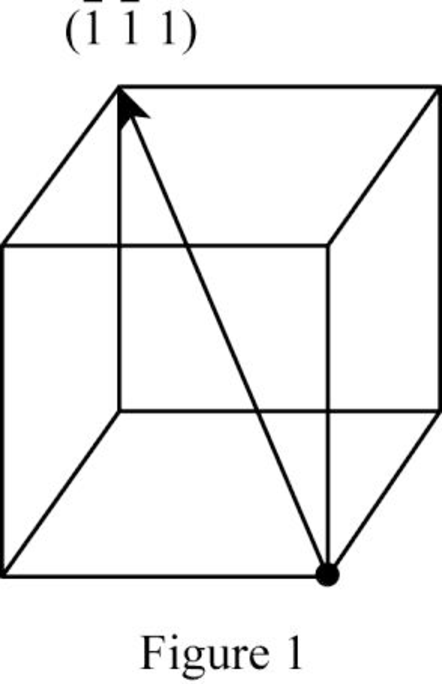
Position coordinates:
For the cubic direction
Repeat distance:
For the cubic direction
(b)
Show the direction vector in a FCC unit cell for the cubic direction
(b)
Explanation of Solution
Show the direction vector in the FCC unit cell for the cubic direction

Position coordinates:
For the cubic direction
Repeat distance:
For the cubic direction
(c)
Show the direction vector in a FCC unit cell for the cubic direction
(c)
Explanation of Solution
Show the direction vector in the FCC unit cell for the cubic direction
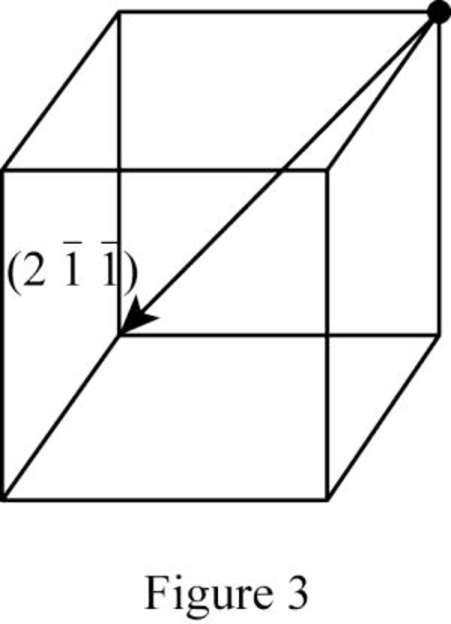
Position coordinates:
For the cubic direction
Repeat distance:
For the cubic direction
(d)
Show the direction vector in a FCC unit cell for the cubic direction
(d)
Explanation of Solution
Show the direction vector in the FCC unit cell for the cubic direction
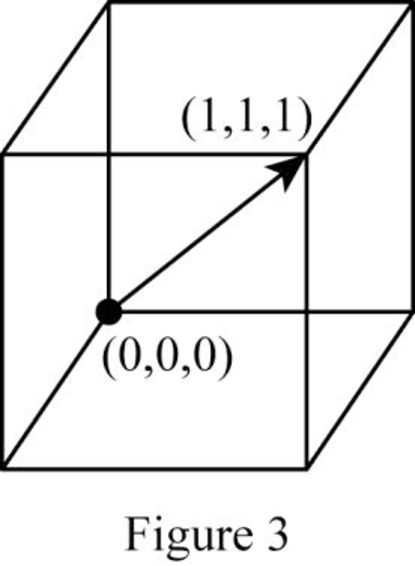
Position coordinates:
For the cubic direction
Repeat distance:
For the cubic direction
(e)
The angle between the direction vectors
(e)
Answer to Problem 30AAP
The angle between the direction vectors
Explanation of Solution
Write the expression to calculate angle between the direction vectors
Here, Miller indices of the cubic plane 1 are
Conclusion:
Substitute 1 for
Thus, the angle between the direction vectors
Want to see more full solutions like this?
Chapter 3 Solutions
Foundations of Materials Science and Engineering
- hand-written solutions only, please.arrow_forwardDetermine the shear flow qqq for the given profile when the shear forces acting at the torsional center are Qy=30Q_y = 30Qy=30 kN and Qz=20Q_z = 20Qz=20 kN. Also, calculate qmaxq_{\max}qmax and τmax\tau_{\max}τmax. Given:Iy=10.5×106I_y = 10.5 \times 10^6Iy=10.5×106 mm4^44,Iz=20.8×106I_z = 20.8 \times 10^6Iz=20.8×106 mm4^44,Iyz=6×106I_{yz} = 6 \times 10^6Iyz=6×106 mm4^44. Additional parameters:αy=0.5714\alpha_y = 0.5714αy=0.5714,αz=0.2885\alpha_z = 0.2885αz=0.2885,γ=1.1974\gamma = 1.1974γ=1.1974. (Check hint: τmax\tau_{\max}τmax should be approximately 30 MPa.)arrow_forwardhand-written solutions only, please.arrow_forward
- In the bending of a U-profile beam, the load path passes through the torsional center C, causing a moment of 25 kNm at the cross-section under consideration. Additionally, the beam is subjected to an axial tensile force of 100 kN at the centroid. Determine the maximum absolute normal stress.(Check hint: approximately 350 MPa, but where?)arrow_forward### Make an introduction to a report of a rocket study project, in the OpenRocket software, where the project consists of the simulation of single-stage and two-stage rockets, estimating the values of the exhaust velocities of the engines used, as well as obtaining the graphs of "altitude", "mass ratio x t", "thrust x t" and "ψ × t".arrow_forwardA 6305 ball bearing is subjected to a steady 5000-N radial load and a 2000-N thrust load and uses a very clean lubricant throughout its life. If the inner race angular velocity is 500 rpm find The equivalent radial load the L10 life and the L50 lifearrow_forward
- Where on the below beam is the Maxiumum Slope likely to occur? C A; Атят Barrow_forwardWhat is the moment of Inertia of this body? What is Ixx, Iyy, and Izzarrow_forwardi need the The shaft is supported by a smooth thrust bearing at AA and a smooth journal bearing at BB. Draw the shear diagram for the shaft. Follow the sign convention.arrow_forward
- 4- In the system shown in the figure, the water velocity in the 12 in. diameter pipe is 8 ft/s. Determine the gage reading at position 1. Elevation 170 ft 1 Elevation 200 ft | 8 ft, 6-in.-diameter, 150 ft, 12-in.-diameter, f = 0.020 f = 0.020 A B Hints: the minor losses should consider the contraction loss at A and the expansion loss at B.arrow_forwardWhat is the moment of Inertia of this body? What is Ixx, Iyy, and Izzarrow_forwardConsider a glass window (Hight = 1.2 m, Width = 2 m). The room thatfaces the window are maintained at 25 o C. The average temperature ofthe inner surface of the window is 5 o C. Calculate the total heat transferrate from through the window a) IdenCfy what type(s) of convecCon is important (circle one). • external forced (Chapter 7)• internal forced (Chapter 8)• natural convecCon (Chapter 9)• boiling and condensaCon (Chapter 10)b) IdenCfy the necessary equaCon(s) needed to solve the problem. c) IdenCfy important fluid properCes you need to solve the problem. d) Calculate the total heat transferred.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





