Chapter 3, Problem 70CR

Many nutritional experts have expressed concern about the high levels of sodium in prepared foods. The following data on sodium content (in milligrams) per frozen meal appeared in the article “Comparison of ‘Light’ Frozen Meals” (Boston Globe, April 24, 1991):

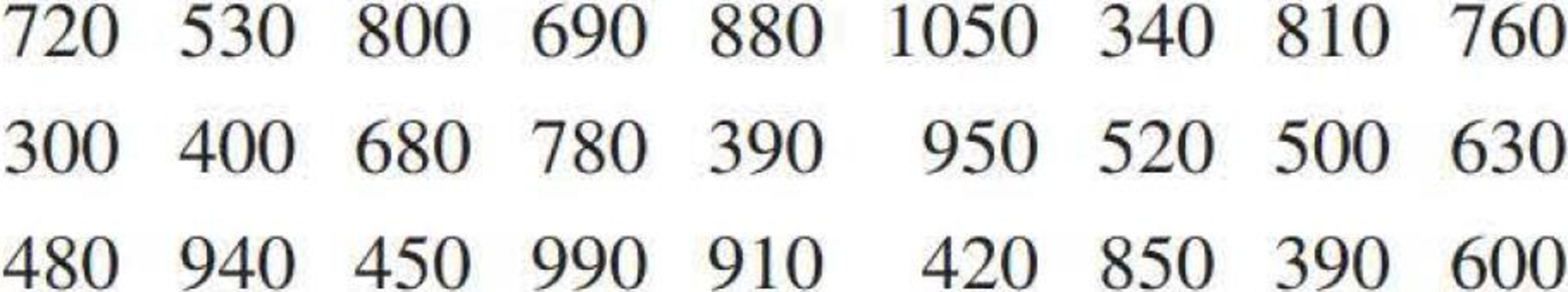
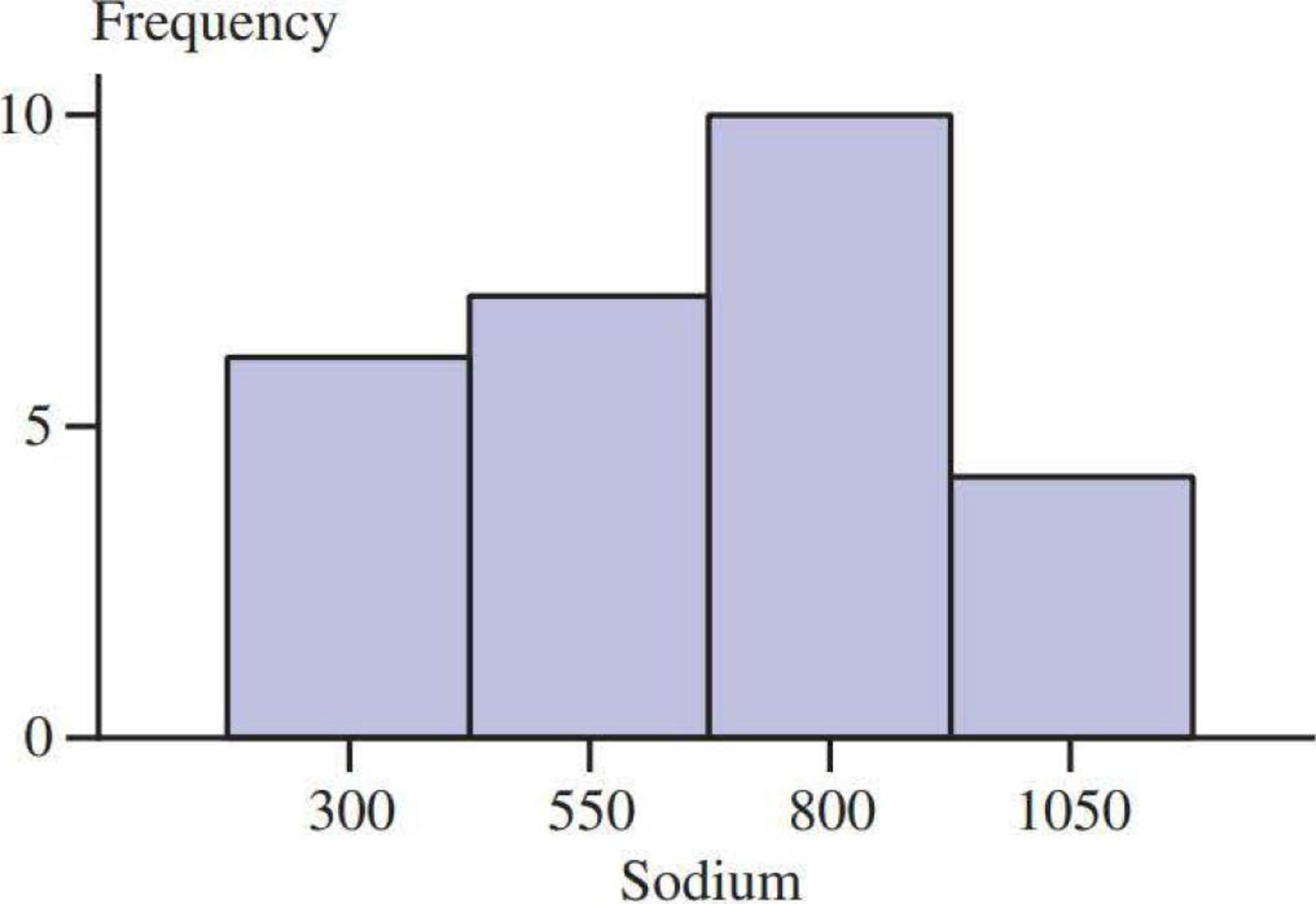
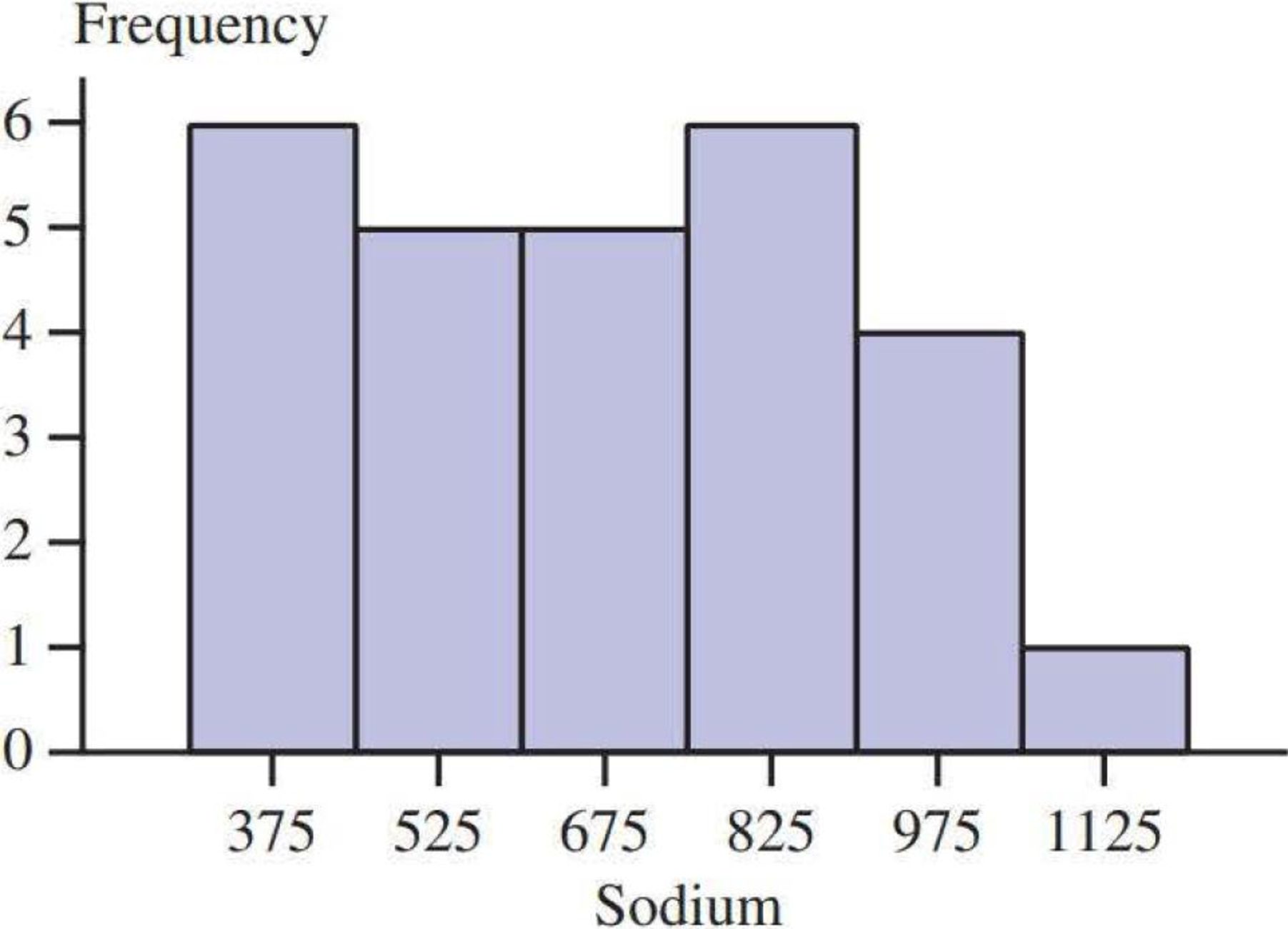
Two histograms for these data are shown below and on the next page.

1. a. Do the two histograms give different impressions about the distribution of values?
2. b. Use each histogram to determine the approximate proportion of observations that are less than 800, and compare to the actual proportion.

To determine

Check whether the interpretations of two histograms are different.

Answer to Problem 70CR

Yes, the two histograms give different impressions about the data of sodium content.

Explanation of Solution

The data represents the sodium content per frozen meal.

Skewness:

In statistics, skewness is a measure by which anyone can measure the asymmetrical behavior of a distribution.

A distribution is said to be symmetric, when its mean, median, and mode are the same. In other words it can be said that, the length of the curve of the left-hand tail will be a mirror image of the right-hand tail.

Therefore, the shape of a distribution can be identified by using the measure of skewness.

Left-skewed:

For a left-skewed distribution, $\text{Mean}<\text{Median}<\text{Mode}$. Moreover, the data will monotonically decrease after attaining the maximum and if the left hand side of the curve is larger than the right hand side, then it is called a left-skewed distribution. This is also called as negatively-skewed distribution.

Right-skewed:

For a right-skewed distribution, $\text{Mean > Median > Mode}$. Moreover, the data will monotonically increase after attaining the maximum and if the right hand side of the curve is larger than the left hand side, then it is called a right-skewed distribution. This is also called as positively-skewed distribution.

Since, the length of the curve of left-hand tail is greater than the right-hand tail, the first histogram indicates that, the distribution of sodium content is negatively skewed.

Since, the length of the curve of right-hand tail is greater than the left-hand tail, the second histogram indicates that, the distribution of sodium content is positively skewed.

Thus, the two histograms give different impressions about the data of sodium content.

To determine

Find the proportion of observations that are less than 800 from the first histogram.

Compute the proportion of observations that are less than 800 from the second histogram.

Answer to Problem 70CR

The proportion of observations that are less than 800 from the first histogram is 0.6667.

The proportion of observations that are less than 800 from the second histogram is 0.6667.

Explanation of Solution

The general formula for the relative frequency or proportion is,

$\text{Relative}\text{Frequency or proportion = }\frac{\text{Frequency}}{\text{Total frequency}}$

First histogram:

From the first histogram display, it can be seen that the frequency of the sodium content that is less than 800 is $\left(6+7+\left(0.5\times 10\right)\right)$

The proportion of sodium content that is less than 800 is obtained as:

Substituting the values of sodium content that is less than “18” as the frequency and total frequency as “27”,

$\begin{array}{c}\left\{\begin{array}{l}\text{Relative}\text{Frequency or proportion}\text{of}\\ \text{sodium content less than 800}\end{array}\right\}=\frac{18}{27}\\ =0.6667\end{array}$

Thus, nearly 66.67% of sodium content is less than 800.

Second histogram:

The Objective is to find the frequency of sodium content that is less than 800.

The class width of class intervals is 150. The fourth interval is between 750 and 900.

The approximate range of less than 800 is 1/3^rd part of the class interval 750 and 900.

Hence, the frequency of the sodium content that is less than 800 is $\left(6+5+5+\left(\frac{6}{3}\right)\right)$.

The proportion of sodium content that is less than 800 is obtained as:

Substituting the values of sodium content that is less than “18” as the frequency and total frequency as “27”,

$\begin{array}{c}\left\{\begin{array}{l}\text{Relative}\text{Frequency or proportion}\text{of}\\ \text{sodium content less than 800}\end{array}\right\}=\frac{18}{27}\\ =0.6667\end{array}$

Thus, nearly 66.67% of sodium content is less than 800.