
Concept explainers
How long after the ball is released from the balcony, the friend has to wait, to start running so that she'll be able to catch the ball exactly 1.00 m above the floor of the court.
Answer to Problem 63QAP
The friend has to wait for 0.25 s after the ball is released and then start running so as to catch the ball at the height of 1.00 m above the floor.
Explanation of Solution
Given info:
The height of the balcony above the court
Initial velocity of the ball
Angle at which the ball is released
Distance of the initial position of the friend from the balcony
Friend's initial velocity
Friend's acceleration
Height at which the ball is caught
Formula used:
The equations of motion for vertical and horizontal motion of the ball can be used to find the time the friend needs to wait.
For vertical motion,
Here,
For horizontal motion of the ball,
Here,
The friend's motion can be analyzed using the equation,
Here,
Calculation:
Assume the origin A to be located at the point just below the balcony, with the x axis parallel to the ground and the positive y axis directed upwards. The height of the balcony from the ground is OA. The friend stands at B initially, and then catches the ball at the point C at a height CD from the ground. This is represented by the diagram shown below.
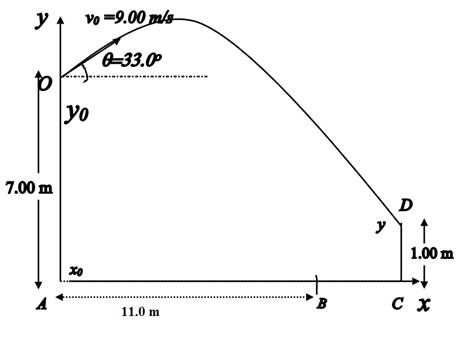
The ball is released with an initial velocity
The vertical motion of the ball is governed by the gravitational force. The acceleration of the ball in the vertical direction is equal to the acceleration of free fall.
Therefore,
The ball makes a vertical displacement from the initial position
Therefore,
Rewrite the equation (1) using the above expression, equation (4).
Substitute the values of the variables in the equation and calculate the value of time of flight t.
Rewrite the equation as a quadratic for t.
Solve for t.
Take the positive root alone.
The ball is in flight for 1.71 s. During this time, the ball travels a horizontal distance
Therefore,
Since point A is directly below the balcony, its x coordinate is
Therefore,
Use equation (5) and the values of the variables in the equation (2) and calculate the value of x.
The friend stands at the position
The horizontal displacement the friend needs to make is given by,
In equation (3), substitute the known values of the variables and calculate the time
Simplify the expression and solve for
The ball takes a time
Calculate the time
Conclusion:
Thus, the friend has to wait for 0.25 s after the ball is released and then start running so as to catch the ball at the height of 1.00 m above the floor.
Want to see more full solutions like this?
Chapter 3 Solutions
COLLEGE PHYSICS-ACHIEVE AC (1-TERM)
- I need help with number 5.arrow_forward3) Use the following system of linear inequalities graphed below to answer the questions. a) Use the graph to write the symbolic form of the system of linear inequalities. b) Is (-4,2) a solution to the system? Explain. 5 -7 -5 -3 -2 0 2 3 4 $ 6 -2 -6 -7arrow_forward) Graph the feasible region subject to the following constraints. x + y ≤ 6 y ≤ 2x x ≥ 0, y ≥ 0 P + xarrow_forward
- Solve the following system of equations: 50x+20y=1800 10x+3y=300arrow_forward> > > we are hiring Salesforce Admin Location: Remote Key Responsibilities: Administer Salesforce Sales & Revenue Cloud (CPQ & Billing) Configure workflows, validation rules & dashboards Automate processes using Flows & Process Builder Collaborate with Sales, Finance & Marketing teams Manage user roles & security Apply: Hr@forcecraver.comarrow_forwardAnswer this questionarrow_forward
- 1. vector projection. Assume, ER1001 and you know the following: ||||=4, 7=-0.5.7. For each of the following, explicitly compute the value. འབ (a) (b) (c) (d) answer. Explicitly compute ||y7||. Explain your answer. Explicitly compute the cosine similarity of and y. Explain your Explicitly compute (x, y). Explain your answer. Find the projection of onto y and the projection of onto .arrow_forward2. Answer the following questions using vectors u and v. --0-0-0 = find the the cosine similarity and the angle between u and v. འརྒྱ (a) (b) find the scalar projection of u onto v. (c) find the projection of u onto v. (d) (e) (f) find the scalar projection of onto u. find the projection of u onto u. find the projection of u onto and the projection of onto . (Hint: find the inner product and verify the orthogonality)arrow_forwardPlease type out answerarrow_forward

 Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage


