
Concept explainers
(i) The x component of the velocity versus time
(ii) The y component of the velocity versus time
(iii) The y component of the acceleration versus time.
Explanation of Solution
Given info:
Magnitude of the initial velocity
Angle made by vi with x- axis
Magnitude of the final velocity
Angle made by vf with x axis
Time interval during which the velocity changes
Formula used:
The components of the velocity vectors along the x and the y directions are given by,
The change in velocity along the x and the y directions is given by,
The components of the acceleration along the x and y directions are given by,
The equation to determine the variation of
The equation to determine the variation of
Calculation:
Resolve the vectors vi and vf along the x and the y axes. This is shown in the diagram below.
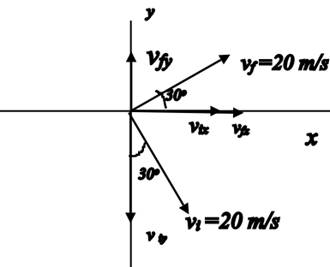
The components of the velocity vector vi are directed along +x and-y axes, hence the y component is assigned a negative sign. Calculate the magnitude of the components substituting the values of the variables in the equation,
The components of the final velocity vector vf are directed along the +x and +y directions, hence the components are positive. Calculate the magnitude of the components of the vector vf using the values of the variables.
Calculate the change in velocity along the x and the y directions.
Calculate the components of the acceleration along the x and the y directions.
Using the values of vix and ax in the equation
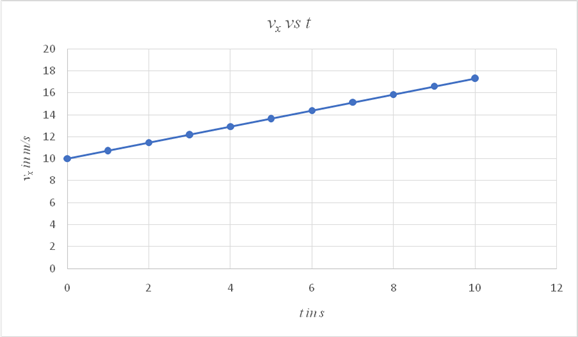
Plot a graph showing the variation of vx with time.
| t in s | vxin m/s |
| 0 | 10 |
| 1 | 10.732 |
| 2 | 11.464 |
| 3 | 12.196 |
| 4 | 12.928 |
| 5 | 13.66 |
| 6 | 14.392 |
| 7 | 15.124 |
| 8 | 15.856 |
| 9 | 16.588 |
| 10 | 17.32 |
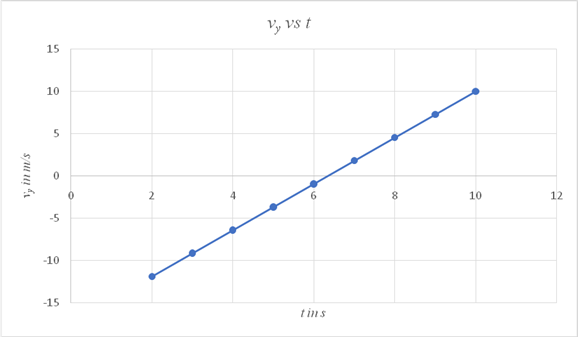
Using the values of viy and ay in the equation
Use the equation in a spread sheet and plot the graph showing the variation of vy with time t.
| X-Values | Y-Values |
| 0 | -17.32 |
| 1 | -14.588 |
| 2 | -11.856 |
| 3 | -9.124 |
| 4 | -6.392 |
| 5 | -3.66 |
| 6 | -0.928 |
| 7 | 1.804 |
| 8 | 4.536 |
| 9 | 7.268 |
| 10 | 10 |
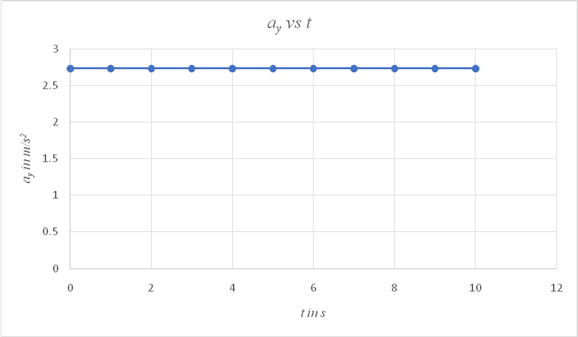
The y component of the acceleration ay is independent of time, since the object's acceleration remains constant during the time interval.
Plot a graph showing the variation of ay with time t.
| t in s | ayin m/s2 |
| 0 | 2.732 |
| 1 | 2.732 |
| 2 | 2.732 |
| 3 | 2.732 |
| 4 | 2.732 |
| 5 | 2.732 |
| 6 | 2.732 |
| 7 | 2.732 |
| 8 | 2.732 |
| 9 | 2.732 |
| 10 | 2.732 |
Conclusion:
The graph showing the variation of vx with time is linear and the value increases from 10 m/s to 17.32 m/s at the end of 10 s.
The graph showing the variation of vy with time is also linear and its value increases from -17.32 m/s to reach a value of 10 m/s at the end of 10 s.
The graph showing the variation of ay with time is a straight line parallel to the time axis, showing that its value is invariant with time.
Thus all the results are consistent with an object moving with a constant acceleration during the time interval of 10s.
Want to see more full solutions like this?
Chapter 3 Solutions
COLLEGE PHYSICS-ACHIEVE AC (1-TERM)
- Please help, everytime I try to input the data only one point shows on the graph. Graph of centripetal force, Fc, versus V E2 from Activity 1. Include a line of best fit and record the equation of the line.arrow_forwardBased on your graph, explain how centripetal force is affected when the hanging mass changes. Does your graph verify the relationship in the equation r = x^i + y^j = r cos ωt I + r sin ωt^j?arrow_forwardDid your experiment results in Data Table 3 verify, to within a reasonable experimental error, the condition of equilibrium of Equation 6: Στanti-clockwise = Στclockwise? Support your response with experimental data. My data shows that they are not equal to each other. So what does this mean? Thanks!arrow_forward
- Please help, everytime I try to input the data only one point shows on the graph. Graph of centripetal force, Fc, versus V E2 from Activity 1. Include a line of best fit and record the equation of the line.arrow_forwardExplain how your experiment met the condition for equilibrium in Equation 4: ΣFvertical = ΣFy = 0.arrow_forwardCan i get answer and solution for this question and can you teach me What we use to get the answer.arrow_forward
- Can i get answer and solution and can you teach me how to get it.arrow_forwardConsider a image that is located 30 cm in front of a lens. It forms an upright image 7.5 cm from the lens. Theillumination is so bright that that a faint inverted image, due to reflection off the front of the lens, is observedat 6.0 cm on the incident side of the lens. The lens is then turned around. Then it is observed that the faint,inverted image is now 10 cm on the incident side of the lens.What is the index of refraction of the lens?arrow_forward2. In class, we discussed several different flow scenarios for which we can make enough assumptions to simplify the Navier-Stokes equations enough to solve them and obtain an exact solution. Consulting the cylindrical form of the Navier-Stokes equations copied below, please answer the following questions. др a 1 a + +0x- + +O₂ = Pgr + μl 18²v, 2 ave ²v₁] az2 + at or r de r Əz dr ar Vodvz др [18 + + +Or + +Vz = Pgz +fl at ar r 20 ôz ôz dr ave дов V,Ve ave +Or + + = pge at dr r 80 Əz + az2 a.) In class, we discussed how the Navier-Stokes equations are an embodiment of Newton's 2nd law, F = ma (where bolded terms are vectors). Name the 3 forces that we are considering in our analysis of fluid flow for this class. др a 10 1 ve 2 av 2200] + +μ or 42 30 b.) If we make the assumption that flow is "fully developed" in the z direction, which term(s) would go to zero? Write the term below, describe what the term means in simple language (i.e. do not simply state "it is the derivative of a with…arrow_forward
- 1. Consult the form of the x-direction Navier-Stokes equation below that we discussed in class. (For this problem, only the x direction equation is shown for simplicity). Note that the equation provided is for a Cartesian coordinate system. In the spaces below, indicate which of the following assumptions would allow you to eliminate a term from the equation. If one of the assumptions provided would not allow you to eliminate a particular term, write "none" in the space provided. du ди at ( + + + 매일) du ди = - Pgx dy др dx ²u Fu u + fl + ax2 ay² az2 - дх - Əz 1 2 3 4 5 6 7 8 9 Assumption Flow is in the horizontal direction (e.g. patient lying on hospital bed) Flow is unidirectional in the x-direction Steady flow We consider the flow to be between two flat, infinitely wide plates There is no pressure gradient Flow is axisymmetric Term(s) in equationarrow_forwardDon't use ai to answer I will report you answerarrow_forwardwhy did the expert subtract the force exerted by the hand and the elbow by the force due to the weight of the hand and forearm and force exerted by the tricep. Does the order matter and how do you determine what to put first. Question 4 AP, CHAPTER 13 FROM BASIC BIOMECHANICS 8TH EDITIONarrow_forward
 University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





