Chapter 3, Problem 63QAP

To determine

How long after the ball is released from the balcony, the friend has to wait, to start running so that she'll be able to catch the ball exactly 1.00 m above the floor of the court.

Answer to Problem 63QAP

The friend has to wait for 0.25 s after the ball is released and then start running so as to catch the ball at the height of 1.00 m above the floor.

Explanation of Solution

Given info:

The height of the balcony above the court

  $y_0=7.00\text{ m}$

Initial velocity of the ball

  $v_0=9.00\text{ m/s}$

Angle at which the ball is released

  $\theta =33.0°$

Distance of the initial position of the friend from the balcony

  $x_1=11.0\text{ m}$

Friend's initial velocity

  $u_0=0\text{ m/s}$

Friend's acceleration

  $a=1.80{\text{ m/s}}^2$

Height at which the ball is caught

  $y=1.00\text{ m}$

Formula used:

The equations of motion for vertical and horizontal motion of the ball can be used to find the time the friend needs to wait.

For vertical motion,

  $\Delta y=v_{0y}t+\frac{1}{2}{a}_y{t}^2$......(1)

Here, $\Delta y$ is the vertical displacement of the ball, $v_{0y}$ is the vertical component of the ball's velocity, t is the time of flight of the ball and $a_y$ is the vertical component of the acceleration.

For horizontal motion of the ball,

  $\Delta x=v_{0x}t+\frac{1}{2}{a}_x{t}^2$......(2)

Here, $\Delta x$ is the horizontal displacement of the ball in time t, $v_{0x}$ is the horizontal component of the ball's velocity and $a_x$ is the acceleration in the horizontal direction.

The friend's motion can be analyzed using the equation,

  $\Delta x=u_0{t}_1+\frac{1}{2}a{t}_1^2$......(3)

Here, $\Delta x$ is the displacement made by the friend, $u_0$ her initial velocity, a her acceleration and $t_1$ is the time she takes to make the displacement.

Calculation:

Assume the origin A to be located at the point just below the balcony, with the x axis parallel to the ground and the positive y axis directed upwards. The height of the balcony from the ground is OA. The friend stands at B initially, and then catches the ball at the point C at a height CD from the ground. This is represented by the diagram shown below.

  

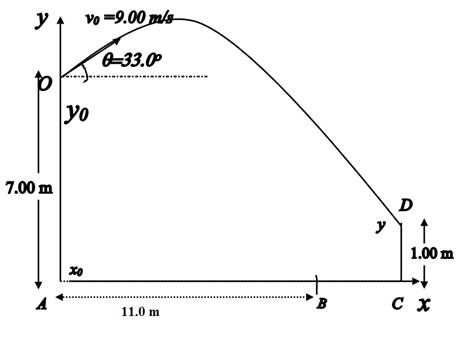
The ball is released with an initial velocity $v_0$ at an angle $\theta$ to the horizontal. Calculate the horizontal and vertical components of the ball's velocity.

  $\begin{array}{c}{v}_{0x}=v_0\cos \theta \\ =\left(9.00\text{ m/s}\right)\left(\cos 33.0°\right)\\ =7.55\text{ m/s}\\ v_{0y}=v_0\sin \theta \\ =\left(9.00\text{ m/s}\right)\left(\sin 33.0°\right)\\ =4.90\text{ m/s}\end{array}$

The vertical motion of the ball is governed by the gravitational force. The acceleration of the ball in the vertical direction is equal to the acceleration of free fall.

Therefore,

  $a_y=g=-9.80{\text{ m/s}}^2$

The ball makes a vertical displacement from the initial position $y_0$ to the final position y.

Therefore,

  $\Delta y=y-y_0$......(4)

Rewrite the equation (1) using the above expression, equation (4).

  $y-y_0=v_{0y}t+\frac{1}{2}{a}_y{t}^2$

Substitute the values of the variables in the equation and calculate the value of time of flight t.

  $\begin{array}{c}y-y_0=v_{0y}t+\frac{1}{2}{a}_y{t}^2\\ \left(1.00\text{ m}\right)-\left(7.00\text{ m}\right)=\left(4.90\text{ m/s}\right)t+\frac{1}{2}\left(-9.80{\text{ m/s}}^2\right)t^2\\ -6.00\text{ m}=\left(4.90\text{ m/s}\right)t-\left(4.90{\text{ m/s}}^2\right)t^2\end{array}$

Rewrite the equation as a quadratic for t.

  $\left(4.90{\text{ m/s}}^2\right)t^2-\left(4.90\text{ m/s}\right)t-6.00\text{ m}=0$

Solve for t.

  $\begin{array}{c}t=\frac{-\left(-4.90\text{ m/s}\right)\pm \sqrt{{\left(-4.90\text{ m/s}\right)}^2-4\left(4.90{\text{ m/s}}^2\right)\left(-6.00\text{ m}\right)}}{2\left(4.90{\text{ m/s}}^2\right)}\\ =\frac{\left(4.90\text{ m/s}\right)\pm \left(11.90\text{ m/s}\right)}{\left(9.80{\text{ m/s}}^2\right)}\end{array}$

Take the positive root alone.

  $t=1.71\text{ s}$

The ball is in flight for 1.71 s. During this time, the ball travels a horizontal distance $\Delta x$, from the position $x_0$ to a position x.

Therefore,

  $\Delta x=x-x_0$......(5)

Since point A is directly below the balcony, its x coordinate is $x_0=0\text{ m}$. No force acts on the ball in the horizontal direction, hence no acceleration acts on the ball in the horizontal direction.

Therefore, $a_x=0{\text{ m/s}}^2$.

Use equation (5) and the values of the variables in the equation (2) and calculate the value of x.

  $\begin{array}{c}\Delta x=v_{0x}t+\frac{1}{2}{a}_x{t}^2\\ x-x_0=v_{0x}t+\frac{1}{2}{a}_x{t}^2\\ x-\left(0\text{ m}\right)=\left(7.55\text{ m/s}\right)\left(1.71\text{ s}\right)+\frac{1}{2}\left(0{\text{ m/s}}^2\right){\left(1.71\text{ s}\right)}^2\\ x=12.91\text{ m}\end{array}$

The friend stands at the position $x_1$ and she needs to make a displacement of $\Delta x$ to reach the position x, with an acceleration a. She takes a time $t_1$ to cover this distance.

The horizontal displacement the friend needs to make is given by,

  $\Delta x=x-x_1$

In equation (3), substitute the known values of the variables and calculate the time $t_1$ she takes to cover the distance.

  $\begin{array}{c}\Delta x=u_0{t}_1+\frac{1}{2}a{t}_1^2\\ x-x_1=u_0{t}_1+\frac{1}{2}a{t}_1^2\\ \left(12.91\text{ m}\right)-\left(11.0\text{ m}\right)=\left(0\text{ m/s}\right)t_1+\frac{1}{2}\left(1.80{\text{ m/s}}^2\right)t_1^2\end{array}$

Simplify the expression and solve for $t_1$.

  $\begin{array}{c}{t}_1=\sqrt{\frac{2\left(1.91\text{ m}\right)}{1.80{\text{ m/s}}^2}}\\ =1.46\text{ s}\end{array}$

The ball takes a time $t=1.71\text{ s}$ to reach point D and the friend needs a time of $t_1=1.46\text{ s}$ to reach the point C. Therefore, she needs to start at a time $\Delta t=t-t_1$ after the ball is released so that she would be able to catch the ball.

Calculate the time $\Delta t$.

  $\begin{array}{c}\Delta t=t-t_1\\ =\left(1.71\text{ s}\right)-\left(1.46\text{ s}\right)\\ =0.25\text{ s}\end{array}$

Conclusion:

Thus, the friend has to wait for 0.25 s after the ball is released and then start running so as to catch the ball at the height of 1.00 m above the floor.