
Concept explainers
(a)
To Draw:
A graph of vx versus time for a projectile and identify the points where the object reaches its highest point and where it hits the ground at the end of its flight.
Explanation of Solution
Introduction:
Consider an object that undergoes a projectile motion. The object is projected with a velocity v at an angle θ to the horizontal. The velocity has an initial horizontal component
For the purpose of drawing a graph showing the variation of vx with time, assume the value of
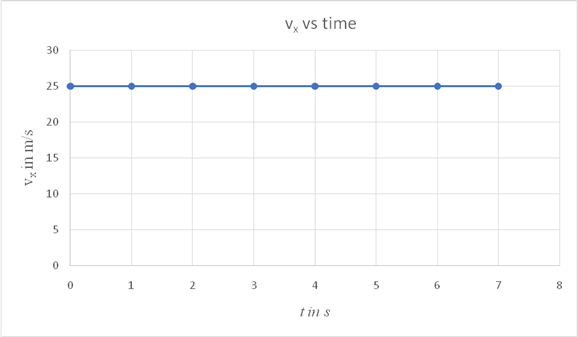
On a spread sheet insert the values as shown and draw a graph as shown.
| t in s | vx in m/s |
| 0 | 25 |
| 1 | 25 |
| 2 | 25 |
| 3 | 25 |
| 4 | 25 |
| 5 | 25 |
| 6 | 25 |
| 7 | 25 |
Conclusion:
The graph is a straight line parallel to the time axis. From the above graph, it is not possible to identify the points where the object reaches its maximum height or when it reaches the ground, since the graph shows no variation of the horizontal component with time.
(b)
To Draw:
A graph of vy versus time for a projectile and identify the points where the object reaches its highest point and where it hits the ground at the end of its flight.
Explanation of Solution
Introduction:
Consider an object that undergoes a projectile motion. The object is projected with a velocity v at an angle θ to the horizontal. The velocity has an initial horizontal component
The projectile after it is launched is under the action of the acceleration of free fall. The vertical component of the projectile varies under the action of the acceleration due to gravity g.
The expression which shows the variation of vy with time is given by,
The acceleration due to gravity g is directed downwards, opposite to the direction of the vertical component of the velocity at the moment of launch. Therefore, it is given a value
Assume, the value of
On a spreadsheet, use the following equation to plot the variation of vy with time.
| t in s | vy in m/s |
| 0 | 30 |
| 0.1 | 29.019 |
| 0.2 | 28.038 |
| 0.3 | 27.057 |
| 0.4 | 26.076 |
| 0.5 | 25.095 |
| 0.6 | 24.114 |
| 0.7 | 23.133 |
| 0.8 | 22.152 |
| 0.9 | 21.171 |
| 1 | 20.19 |
| 1.1 | 19.209 |
| 1.2 | 18.228 |
| 1.3 | 17.247 |
| 1.4 | 16.266 |
| 1.5 | 15.285 |
| 1.6 | 14.304 |
| 1.7 | 13.323 |
| 1.8 | 12.342 |
| 1.9 | 11.361 |
| 2 | 10.38 |
| 2.1 | 9.399 |
| 2.2 | 8.418 |
| 2.3 | 7.437 |
| 2.4 | 6.456 |
| 2.5 | 5.475 |
| 2.6 | 4.494 |
| 2.7 | 3.513 |
| 2.8 | 2.532 |
| 2.9 | 1.551 |
| 3 | 0.57 |
| 3.1 | -0.411 |
| 3.2 | -1.392 |
| 3.3 | -2.373 |
| 3.4 | -3.354 |
| 3.5 | -4.335 |
| 3.6 | -5.316 |
| 3.7 | -6.297 |
| 3.8 | -7.278 |
| 3.9 | -8.259 |
| 4 | -9.24 |
| 4.1 | -10.221 |
| 4.2 | -11.202 |
| 4.3 | -12.183 |
| 4.4 | -13.164 |
| 4.5 | -14.145 |
| 4.6 | -15.126 |
| 4.7 | -16.107 |
| 4.8 | -17.088 |
| 4.9 | -18.069 |
| 5 | -19.05 |
| 5.1 | -20.031 |
| 5.2 | -21.012 |
| 5.3 | -21.993 |
| 5.4 | -22.974 |
| 5.5 | -23.955 |
| 5.6 | -24.936 |
| 5.7 | -25.917 |
| 5.8 | -26.898 |
| 5.9 | -27.879 |
| 6 | -28.86 |
| 6.1 | -29.841 |
| 6.2 | -30.822 |
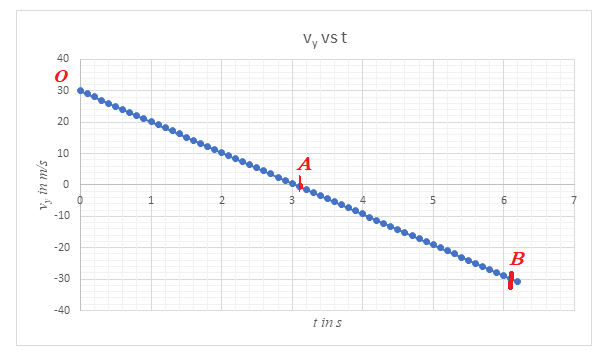
From the graph, the following points are noted:
1.The maximum positive value of vy is at point O, which the point at which it is launched.
2. As the object rises, the vertical component of its velocity reduces under the action of acceleration due to gravity g. When it reaches the maximum height, this component attains a value zero. This is seen from the graph as point A. The time taken by this projectile to reach its maximum height is seen to be equal to 3.05 s.
3. As the object descends from the position of maximum height, the vertical component of its velocity is directed downwards and hence it has a negative value. Its value increases as it moves downwards, since now, the vertical component vy and the acceleration due to gravity are both directed downwards. When it hits the ground, the vertical component vy has a magnitude of 30 m/s and it is directed downwards, hence negative. Point B represents the point when it reaches the ground. The total time of flight from the graph is 6.1 s.
Conclusion:
The object with a vertical component of magnitude 30 m/s, reaches the position of maximum height in time 3.05 s and reaches the ground after 6.1 s. The graph varies linearly with time. The gradient of the graph is equal to g which has a value
(c)
To Draw:
A graph showing the variation of ax with time.
Explanation of Solution
Introduction:
A projectile travels a parabolic path under the action of acceleration due to gravity, if no air resistance acts on it.
The only force acting on the projectile is the gravitational force, which is directed downwards, towards the center of the Earth. This force is constant at points close to the surface of the earth. Since it is directed towards the ground, it has no component along the horizontal direction. Hence,
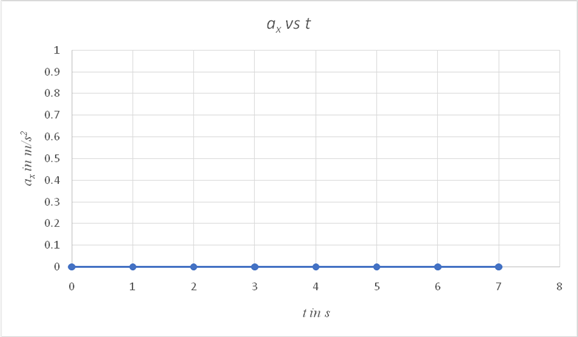
On a spreadsheet, use
| tin s | ax in m/s2 |
| 0 | 0 |
| 1 | 0 |
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 0 |
| 6 | 0 |
| 7 | 0 |
Conclusion:
Since the only force acting on the projectile is the gravitational force and it has no component along the horizontal direction, the horizontal component of its acceleration is zero at all times, as shown in the graph.
(d)
To Draw:
A graph showing the variation of ay with time.
Explanation of Solution
Introduction:
A projectile travel in a parabolic path under the action of acceleration due to gravity. If no air resistance acts on the object, the only force acting on it is the gravitational force. Hence the vertical component of the object's acceleration is
The gravitational force is a constant at points close to the surface of the earth. The acceleration due to gravity has a constant value of
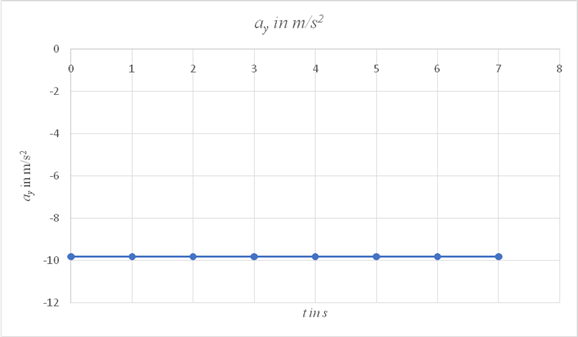
On a spreadsheet, use the expression
| tin s | ay in m/s2 |
| 0 | -9.81 |
| 1 | -9.81 |
| 2 | -9.81 |
| 3 | -9.81 |
| 4 | -9.81 |
| 5 | -9.81 |
| 6 | -9.81 |
| 7 | -9.81 |
Conclusion:
The graph of ay vs time is a straight line parallel to the time axis and has a constant value of
Want to see more full solutions like this?
Chapter 3 Solutions
COLLEGE PHYSICS LL W/ 6 MONTH ACCESS
- 3) Two bumper cars of masses 600 kg and 900 kg travelling (on a smooth surface) with velocities 8m/s and 4 m/s respectively, have a head on collision. If the coefficient of restitution is 0.5. a) What sort of collision is this? b) Calculate their velocities immediately after collision. c) If the coefficient of restitution was 1 instead of 0.5, what is the amount of energy lost during collision?arrow_forwardThe rectangular loop of wire shown in the figure (Figure 1) has a mass of 0.18 g per centimeter of length and is pivoted about side ab on a frictionless axis. The current in the wire is 8.5 A in the direction shown. Find the magnitude of the magnetic field parallel to the y-axis that will cause the loop to swing up until its plane makes an angle of 30.0 ∘ with the yz-plane. Find the direction of the magnetic field parallel to the y-axis that will cause the loop to swing up until its plane makes an angle of 30.0 ∘ with the yz-plane.arrow_forwardGive a more general expression for the magnitude of the torque τ. Rewrite the answer found in Part A in terms of the magnitude of the magnetic dipole moment of the current loop m. Define the angle between the vector perpendicular to the plane of the coil and the magnetic field to be ϕ, noting that this angle is the complement of angle θ in Part A. Give your answer in terms of the magnetic moment mm, magnetic field B, and ϕ.arrow_forward
- Calculate the electric and magnetic energy densities at thesurface of a 3-mm diameter copper wire carrying a 15-A current. The resistivity ofcopper is 1.68×10-8 Ω.m.Prob. 18, page 806, Ans: uE= 5.6 10-15 J/m3 uB= 1.6 J/m3arrow_forwardA 15.8-mW laser puts out a narrow beam 2.0 mm in diameter.Suppose that the beam is in free space. What is the rms value of E in the beam? What isthe rms value of B in the beam?Prob. 28, page 834. Ans: Erms= 1380 V/m, Brms =4.59×10-6 Tarrow_forwardA 4.5 cm tall object is placed 26 cm in front of a sphericalmirror. It is desired to produce a virtual image that is upright and 3.5 cm tall.(a) What type of mirror should be used, convex, or concave?(b) Where is the image located?(c) What is the focal length of the mirror?(d) What is the radius of curvature of the mirror?Prob. 25, page 861. Ans: (a) convex, (b) di= -20.2 cm, i.e. 20.2 cm behind the mirror,(c) f= -90.55 cm, (d) r= -181.1 cm.arrow_forward
- A series RCL circuit contains an inductor with inductance L=3.32 mH, and a generator whose rms voltage is 11.2 V. At a resonant frequencyof 1.25 kHz the average power delivered to the circuit is 26.9 W.(a) Find the value of the capacitance.(b) Find the value of the resistance.(c) What is the power factor of this circuit?Ans: C=4.89 μF, R=4.66 Ω, 1.arrow_forwardA group of particles is traveling in a magnetic field of unknown magnitude and direction. You observe that a proton moving at 1.70 km/s in the +x-direction experiences a force of 2.06×10−16 N in the +y-direction, and an electron moving at 4.40 km/s in the −z-direction experiences a force of 8.10×10−16 N in the +y-direction. What is the magnitude of the magnetic force on an electron moving in the −y-direction at 3.70 km/s ? What is the direction of this the magnetic force? (in the xz-plane)arrow_forwardA particle with a charge of −5.20 nC is moving in a uniform magnetic field of B =−( 1.22 T )k^. The magnetic force on the particle is measured to be F=−( 3.50×10−7 N )i^+( 7.60×10−7 N )j^. Calculate the x component of the velocity of the particle.arrow_forward
- Is it possible for average velocity to be negative?a. Yes, in cases when the net displacement is negative.b. Yes, if the body keeps changing its direction during motion.c. No, average velocity describes only magnitude and not the direction of motion.d. No, average velocity describes only the magnitude in the positive direction of motion.arrow_forwardTutorial Exercise An air-filled spherical capacitor is constructed with an inner-shell radius of 6.95 cm and an outer-shell radius of 14.5 cm. (a) Calculate the capacitance of the device. (b) What potential difference between the spheres results in a 4.00-μC charge on the capacitor? Part 1 of 4 - Conceptualize Since the separation between the inner and outer shells is much larger than a typical electronic capacitor with separation on the order of 0.1 mm and capacitance in the microfarad range, we expect the capacitance of this spherical configuration to be on the order of picofarads. The potential difference should be sufficiently low to avoid sparking through the air that separates the shells. Part 2 of 4 - Categorize We will calculate the capacitance from the equation for a spherical shell capacitor. We will then calculate the voltage found from Q = CAV.arrow_forwardI need help figuring out how to do part 2 with the information given in part 1 and putting it in to the simulation. ( trying to match the velocity graph from the paper onto the simulation to find the applied force graph) Using this simulation https://phet.colorado.edu/sims/cheerpj/forces-1d/latest/forces-1d.html?simulation=forces-1d.arrow_forward
 Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning
An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





