Chapter 3, Problem 42P

To determine

The velocity of a rocket launched at ${40.0}^{\text{o}}$ North latitude along East, with respect to the ground and the advantage in firing the rocket from a site closer to the equator.

Answer to Problem 42P

The velocity of a rocket launched at ${40.0}^{\text{o}}$ North latitude along East, with respect to the ground is found to be $1.0645\times {\text{10}}^4\text{ m/s}$ . If the rocket is launched from a point close to the equator, the speed which is to be imparted to it at the ground would beless by $108\text{ m/s}$ , which would save on fuel costs.

Explanation of Solution

Given info:

The latitude of the point of launch, $\theta =40.0°$

Velocity of the rocket with respect to the center of the Earth, $v_R=11.0\text{ km/s}$

Formula used:

The velocity of the ground with respect to the ground $v_G$ is given by

  $v_G=\frac{2\pi r}{T}$.....(1)

Here, r is the radius of the circular path traversed by the particle and T is the time taken for it to complete one rotation.

Calculation:

The point of launch is at a latitude ${40.0}^{\text{o}}$ North and as the Earth rotates around its axis, the ground moves in a circular path of radius r ,with its center on the Earth’s axis of rotation.

This is shown in the diagram below:

  

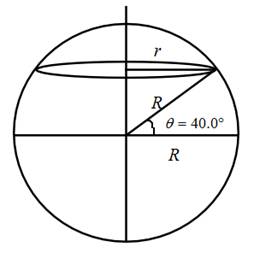
From the diagram, it can be seen that,

  $r=R\cos \theta$.....(2)

Here, R is the radius of the Earth, which has a value $6.37\times {10}^3\text{km}$ .

Express the radius of the Earth in meters.

  $\begin{array}{c}R=\left(6.37\times {10}^3\text{km}\right)\left(\frac{{10}^3\text{ m}}{1\text{ km}}\right)\\ =6.37\times {10}^6\text{m}\end{array}$

Calculate the value of r by substituting the values of R and $\theta$ in equation (2).

  $\begin{array}{c}r=R\cos \theta \\ =\left(6.37\times {10}^6\text{m}\right)\left(\cos 40.0°\right)\\ =4.88\times {10}^6\text{m}\end{array}$

The Earth takes 24 h to complete one rotation. In the same time, the point on the ground completes its circular path of radius r .

Calculate the time T taken by the point on the ground to go once around the circular path of radius r in seconds.

  $\begin{array}{c}T=\left(24\text{ h}\right)\left(\frac{3600\text{ s}}{1\text{ h}}\right)\\ =8.64\times {10}^4\text{s}\end{array}$

Substitute the values of r and T in equation (1) and calculate the magnitude of the ground’s velocity relative to the center of the Earth.

  $\begin{array}{c}{v}_G=\frac{2\pi r}{T}\\ =\frac{2\pi \left(4.88\times {10}^6\text{m}\right)}{\left(8.64\times {10}^4\text{s}\right)}\\ =3.55\times {10}^2\text{m/s}\end{array}$

The Earth rotates from west towards east. Hence, the point where the rocket is launched has a velocity $3.55\times {10}^2\text{m/s}$ directed eastwards at the instant of launch.

The rocket is launched with a speed of 11.0 km/s eastward with respect to the center of Earth.

Express the speed $v_R$ of the rocket with respect to the center of the Earth in m/s.

  $\begin{array}{c}{v}_R=\left(11.0\text{ km/s}\right)\left(\frac{{10}^3\text{m}}{1\text{ km}}\right)\\ =1.10\times {10}^4\text{m/s}\end{array}$

The Ground rotates with a speed $v_G$ eastwards with respect to the center of the Earth.

The speed $v_{RG}$ of the rocket with respect to the ground is given by,

  $v_{RG}=v_R-v_G$

Calculate the speed $v_{RG}$ by substituting the given values in the above equation.

  $\begin{array}{c}{v}_{RG}=v_R-v_G\\ =\left(1.10\times {10}^4\text{m/s}\right)-\left(3.55\times {10}^2\text{m/s}\right)\\ =1.0645\times {\text{10}}^4\text{ m/s}\end{array}$

If the rocket is launched at a point near the equator, the ground moves in a circular path equal to the radius of the Earth. Calculate the speed of the ground at the equator using equation (1) in the following form:

  ${\left(v_G\right)}_{Eq}=\frac{2\pi R}{T}$

Substitute the given values in the above expression and calculate the velocity of the ground with respect to the center of Earth at equator.

  $\begin{array}{c}{\left(v_G\right)}_{Eq}=\frac{2\pi R}{T}\\ =\frac{2\pi \left(6.37\times {10}^6\text{m}\right)}{\left(8.64\times {10}^4\text{s}\right)}\\ =4.63\times {10}^2\text{m/s}\end{array}$

The speed that needs to be imparted to the rocket at equator is the relative velocity of the rocket with respect to the ground.

  $\begin{array}{c}{\left(v_{RG}\right)}_{Eq}=v_R-{\left(v_G\right)}_{Eq}\\ =\left(1.10\times {10}^4\text{m/s}\right)-\left(4.63\times {10}^2\text{m/s}\right)\\ =1.0537\times {\text{10}}^4\text{ m/s}\end{array}$

The difference in the velocities of the rocket when launched at 40.0^o latitude and at equator is given by,

  $\Delta v=v_{RG}-{\left(v_{RG}\right)}_{Eq}$

Substitute the given values in the above expression:

  $\begin{array}{c}\Delta v=v_{RG}-{\left(v_{RG}\right)}_{Eq}\\ =\left(1.0645\times {10}^4\text{m/s}\right)-\left(1.0537\times {\text{10}}^4\text{ m/s}\right)\\ =108\text{ m/s}\end{array}$

Conclusion:

Thus, the velocity of a rocket launched at 40.0^oNorth latitude along East, with respect to the ground is found to be $1.0645\times {\text{10}}^4\text{ m/s}$ . If the rocket is launched from a point close to the equator, the speed which is to be imparted to it at the ground would be less by $108\text{ m/s}$ , which would save on fuel costs.