Chapter 3, Problem 33E

Program Plan Intro

a.

K-Map:

• K-Map stands for Karnaugh Map which is used to reduce the logic functions more easily and quickly.
• It will minimize the Boolean expressions without using Boolean algebra theorems.
• By using K-Map, the Boolean expressions with two to four variables are easily reduced.

Explanation of Solution

Simplification of Boolean expression using K-Map:

 Given:

 $\begin{array}{c}\text{F}\left(\text{x, y, z}\right)=\text{w'}\cdot \text{x'}\cdot \text{y'}\cdot \text{z' + w'}\cdot \text{x'}\cdot \text{y}\cdot \text{z' + w'}\cdot \text{x}\cdot \text{y'}\cdot \text{z + }\\ \text{ w'}\cdot \text{x}\cdot \text{y}\cdot \text{z + w'}\cdot \text{x}\cdot \text{y}\cdot \text{z' + w}\cdot \text{x'}\cdot \text{y'}\cdot \text{z' + w}\cdot \text{x'}\cdot \text{y}\cdot \text{z'}\end{array}$

 The K-Map for the given expression is as follows:

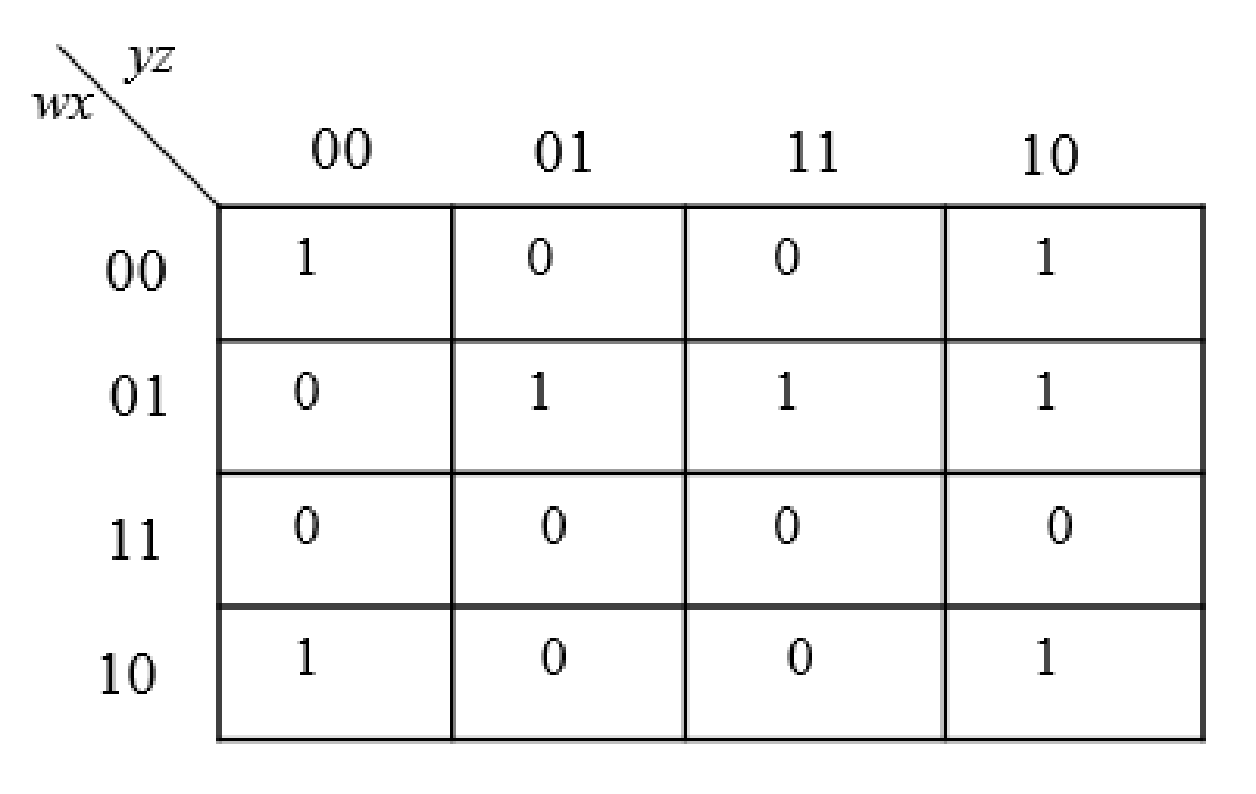
 The following steps are used to obtain the simplified Boolean expressions.

 Step1:

 Then group another possible 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.

     $\begin{array}{c}\text{F = w'}\cdot \text{x'}\cdot \text{y'}\cdot \text{z' + w'}\cdot \text{x'}\cdot \text{y}\cdot \text{z' + w}\cdot \text{x'}\cdot \text{y'}\cdot \text{z' + w}\cdot \text{x'}\cdot \text{y}\cdot \text{z'}\\ \text{= w'}\cdot \text{x'}\cdot \text{z'}\cdot \left(\text{y'+y}\right)\text{ + w}\cdot \text{x'}\cdot \text{z'}\cdot \left(\text{y'+y}\right)\\ =\text{w'}\cdot \text{x'}\cdot \text{z'}\cdot \left(\text{1}\right)\text{ + w}\cdot \text{x'}\cdot \text{z'}\cdot \left(\text{1}\right)\\ =\text{w'}\cdot \text{x'}\cdot \text{z' + w}\cdot \text{x'}\cdot \text{z'}\end{array}$

        $\begin{array}{c}=\left(\text{w' + w}\right)\cdot \text{x'}\cdot \text{z'}\\ =\left(\text{1}\right)\cdot \text{x'}\cdot \text{z'}\\ =\text{x'}\cdot \text{z'}\end{array}$

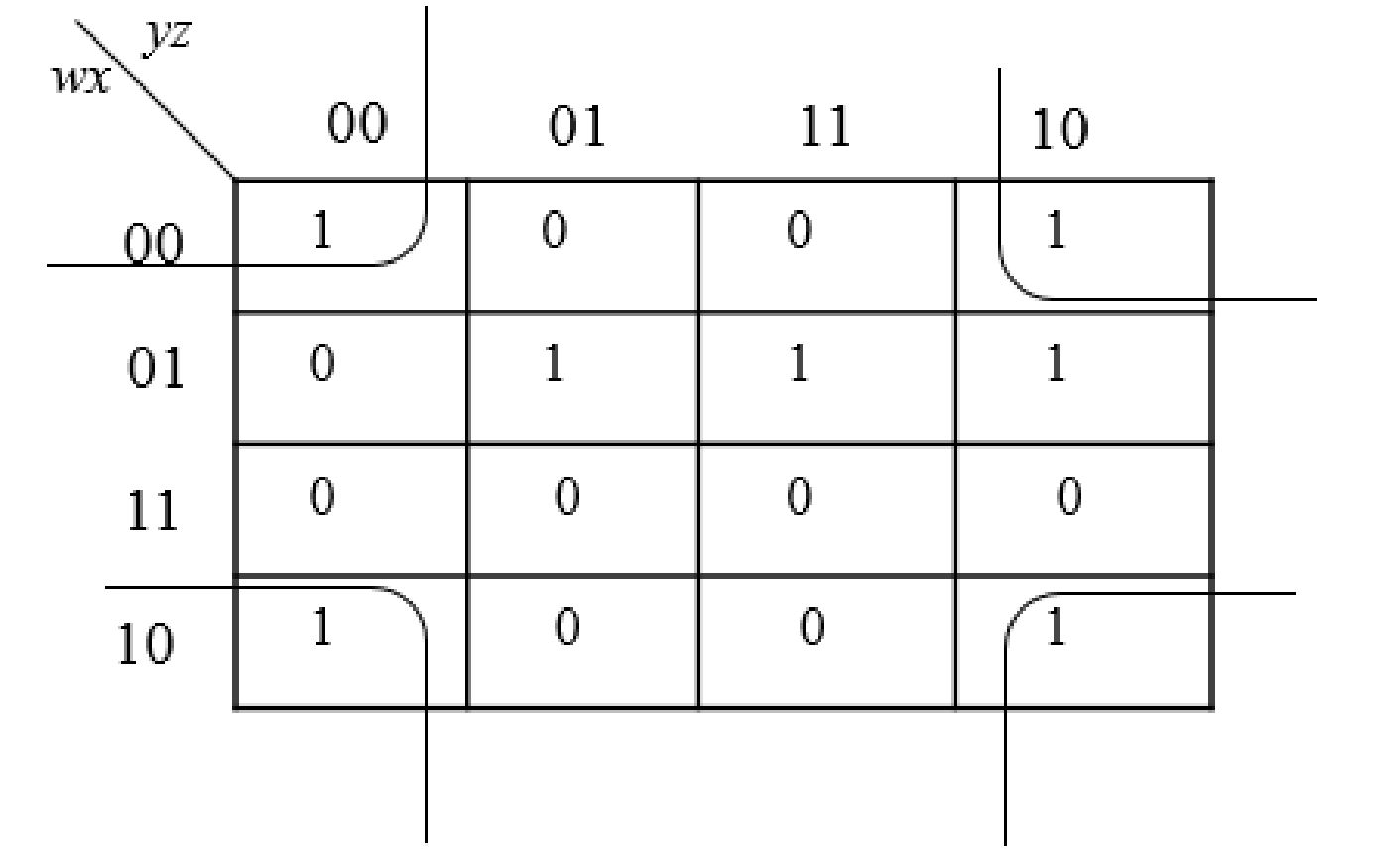
 Step2:

  The group the 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.

     $\begin{array}{c}\text{F = w'}\cdot \text{x}\cdot \text{y'}\cdot \text{z + w'}\cdot \text{x}\cdot \text{y}\cdot \text{z}\\ \text{= w'}\cdot \text{x}\cdot \text{z}\cdot \left(\text{y'+y}\right)\\ =\text{w'}\cdot \text{x}\cdot \text{z}\cdot \left(\text{1}\right)\\ =\text{w'}\cdot \text{x}\cdot \text{z}\end{array}$

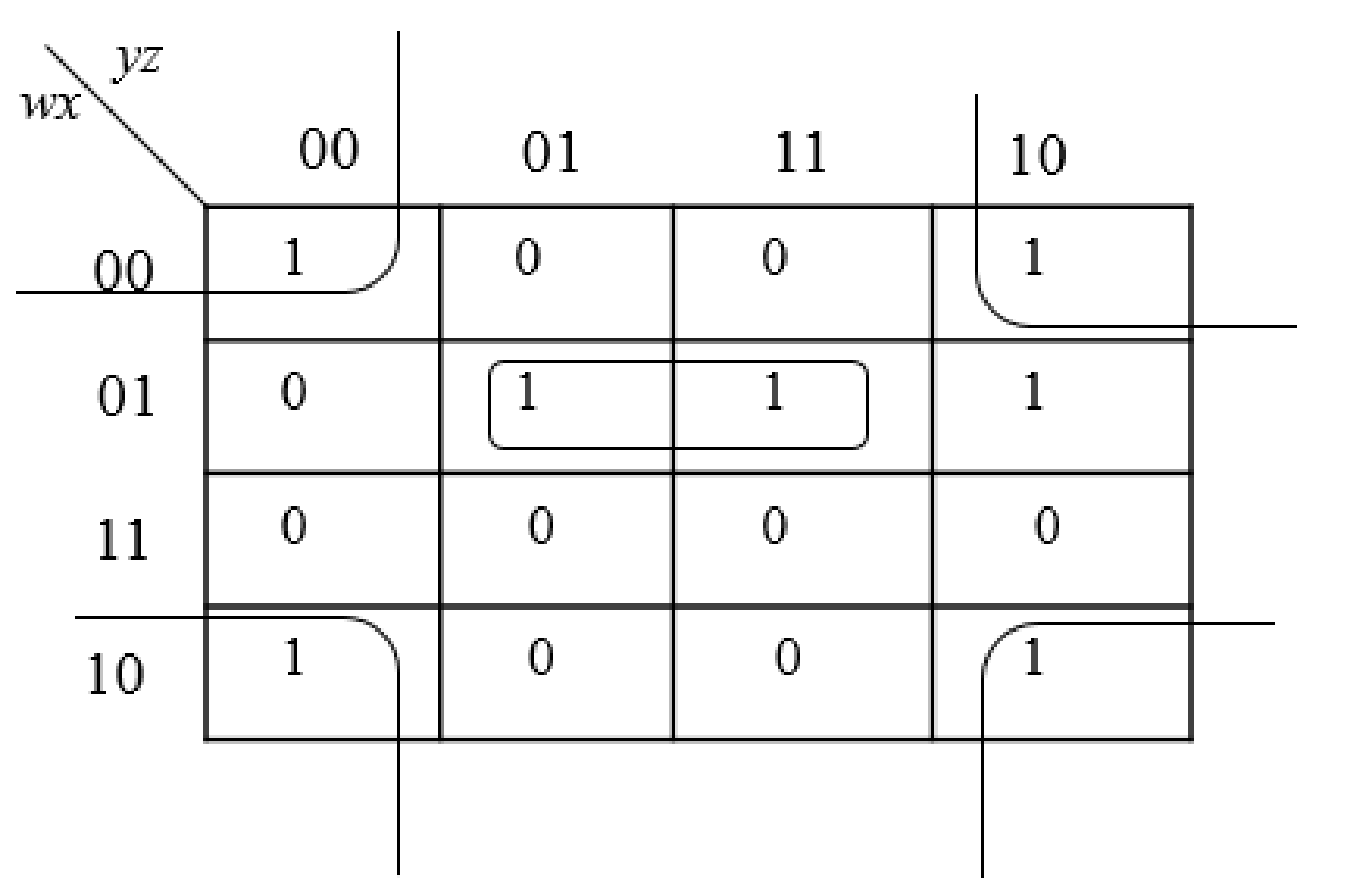
 Step3:

  The group the 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.

     $\begin{array}{c}\text{F = w'}\cdot \text{x}\cdot \text{y}\cdot \text{z + w'}\cdot \text{x}\cdot \text{y}\cdot \text{z'}\\ \text{= w'}\cdot \text{x}\cdot \text{y}\cdot \left(\text{z'+z}\right)\\ =\text{w'}\cdot \text{x}\cdot \text{y}\cdot \left(\text{1}\right)\\ =\text{w'}\cdot \text{x}\cdot \text{y}\end{array}$

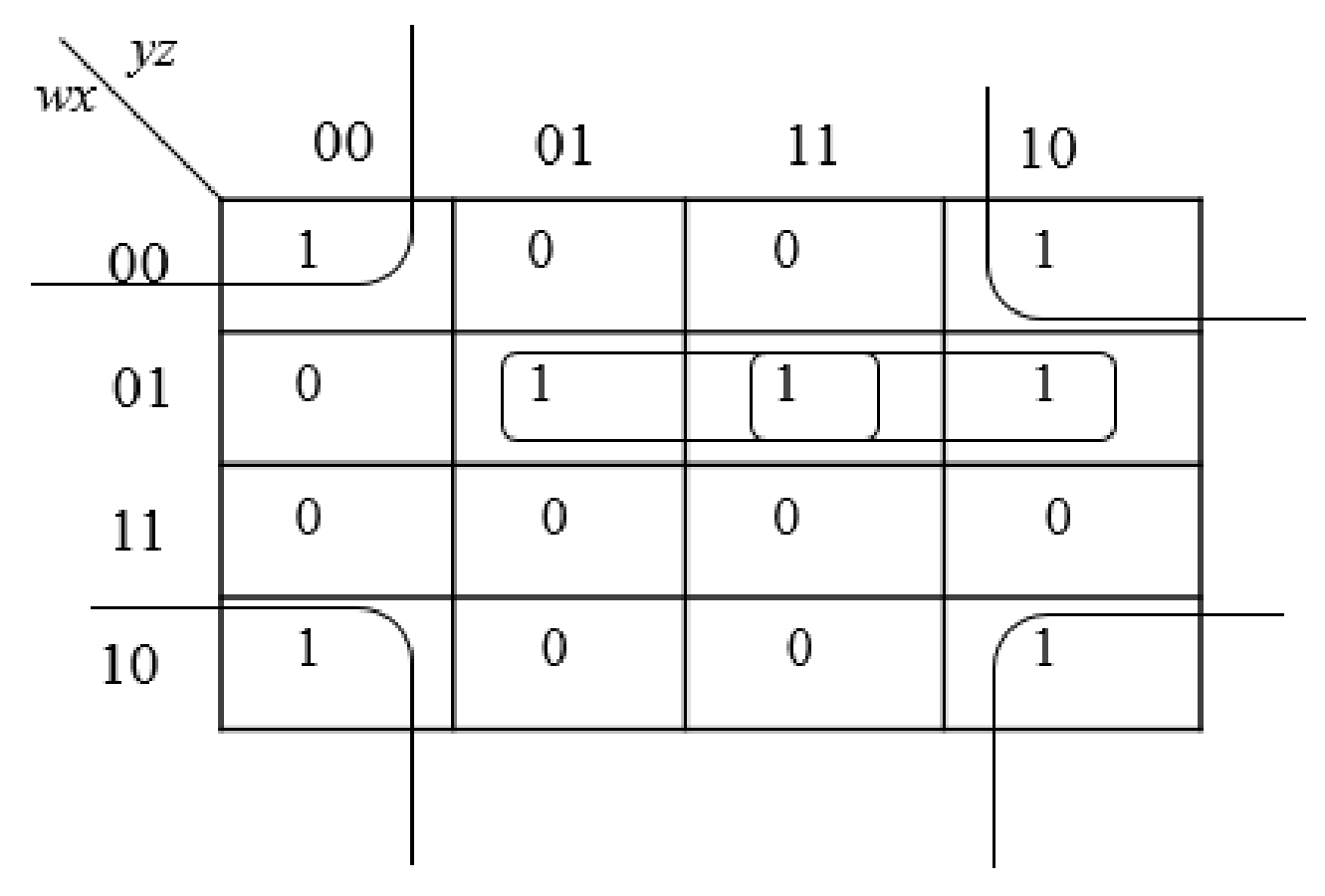
 Step4:

 Group all the expressions

 $\text{F = x'}\cdot \text{z' + w'}\cdot \text{x}\cdot \text{z + w'}\cdot \text{x}\cdot \text{y}$

 Therefore, the simplified expression is “$F=x\text{'}\cdot z\text{'}+w\text{'}\cdot x\cdot z+w\text{'}\cdot x\cdot y$”.

Program Plan Intro

b.

K-Map:

• K-Map stands for Karnaugh Map which is used to reduce the logic functions more easily and quickly.
• It will minimize the Boolean expressions without using Boolean algebra theorems.
• By using K-Map, the Boolean expressions with two to four variables are easily reduced.

Explanation of Solution

Simplification of Boolean expression using K-Map:

 Given:

 $\text{F}\left(\text{x, y, z}\right)=\text{w'}\cdot \text{x'}\cdot \text{y'}\cdot \text{z' + w'}\cdot \text{x'}\cdot \text{y'}\cdot \text{z + w}\cdot \text{x'}\cdot \text{y'}\cdot \text{z + w}\cdot \text{x'}\cdot \text{y}\cdot \text{z' + w}\cdot \text{x'}\cdot \text{y'}\cdot \text{z'}$

 The K-Map for the given expression is as follows:

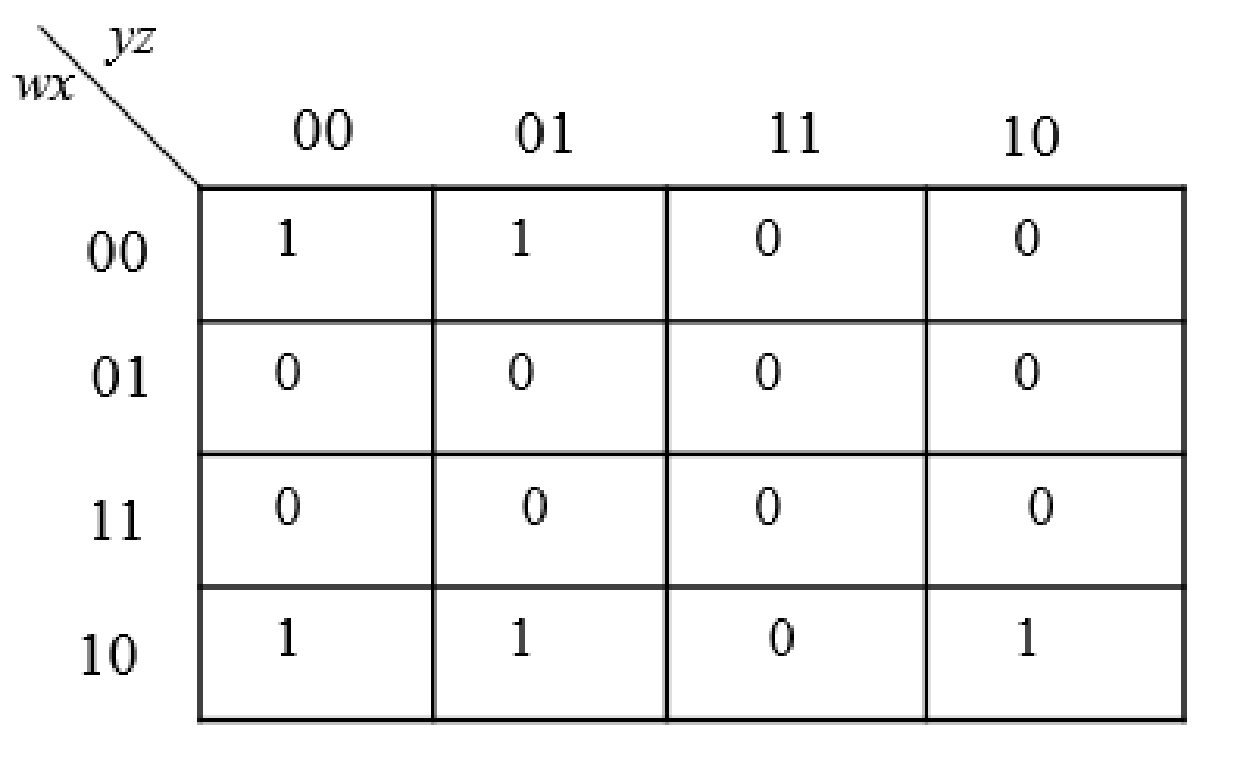
 The following steps are used to obtain the simplified Boolean expressions.

 Step1:

 The group the 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.

     $\begin{array}{c}\text{F = w'}\cdot \text{x'}\cdot \text{y'}\cdot \text{z' + w'}\cdot \text{x'}\cdot \text{y'}\cdot \text{z + w}\cdot \text{x'}\cdot \text{y'}\cdot \text{z' + w}\cdot \text{x'}\cdot \text{y'}\cdot \text{z}\\ \text{= w'}\cdot \text{x'}\cdot \text{y'}\cdot \left(\text{z' + z}\right)\text{+ w}\cdot \text{x'}\cdot \text{y'}\cdot \left(\text{z' + z}\right)\text{}\\ =\text{w'}\cdot \text{x'}\cdot \text{y'}\cdot \left(\text{1}\right)\text{+ w}\cdot \text{x'}\cdot \text{y'}\cdot \left(\text{1}\right)\\ =\text{w'}\cdot \text{x'}\cdot \text{y'}\text{+ w}\cdot \text{x'}\cdot \text{y'}\end{array}$

        $\begin{array}{c}=\left(\text{w' + w}\right)\cdot \text{x'}\cdot \text{y'}\\ =\left(\text{1}\right)\cdot \text{x'}\cdot \text{y'}\\ =\text{x'}\cdot \text{y'}\end{array}$

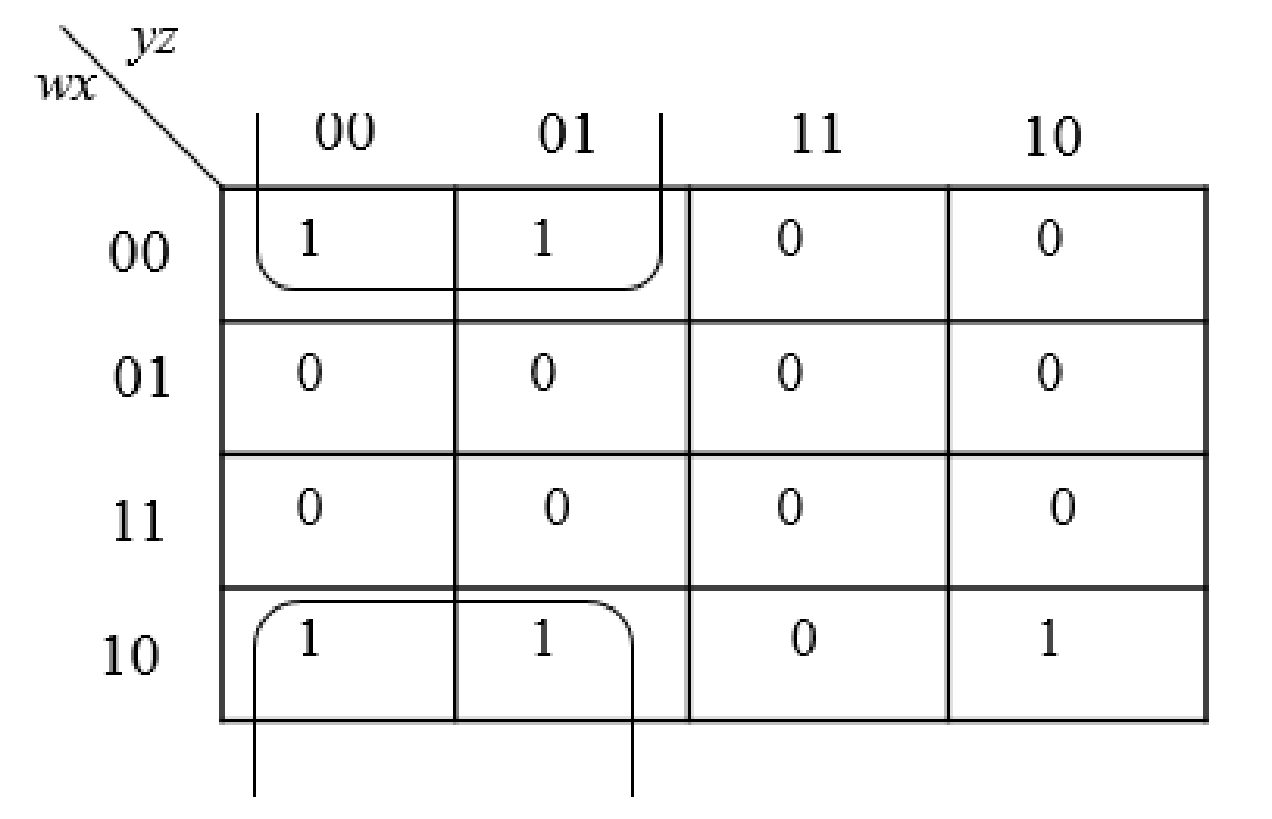
 Step2:

 The group the 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.

     $\begin{array}{c}\text{F = w}\cdot \text{x'}\cdot \text{y'}\cdot \text{z' + w}\cdot \text{x'}\cdot \text{y}\cdot \text{z'}\\ \text{= w}\cdot \text{x'}\cdot \text{z'}\cdot \left(\text{y' + y}\right)\text{}\\ =\text{w}\cdot \text{x'}\cdot \text{z'}\cdot \left(\text{1}\right)\\ =\text{w}\cdot \text{x'}\cdot \text{z'}\end{array}$

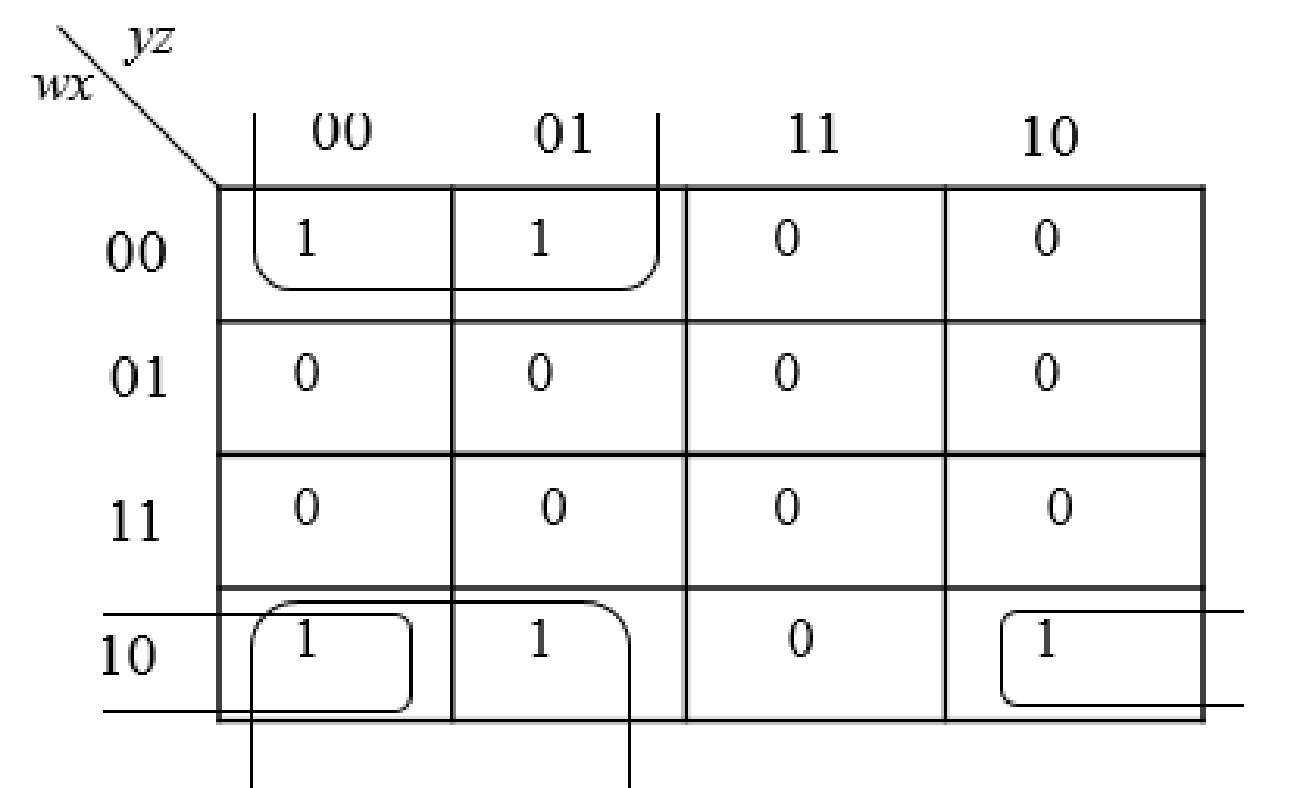
 Step3:

 Group all the expressions

 $\text{F = x'}\cdot \text{y' + w}\cdot \text{x'}\cdot \text{z'}$

 Therefore, the simplified expression is “$F=x\text{'}\cdot y\text{'}+w\cdot x\text{'}\cdot z\text{'}$”.

Program Plan Intro

c.

K-Map:

• K-Map stands for Karnaugh Map which is used to reduce the logic functions more easily and quickly.
• It will minimize the Boolean expressions without using Boolean algebra theorems.
• By using K-Map, the Boolean expressions with two to four variables are easily reduced.

Explanation of Solution

Simplification of Boolean expression using K-Map:

 Given:

 $\begin{array}{c}\text{F}\left(\text{x, y, z}\right)=\text{y'}\cdot \text{z + w}\cdot \text{y' + w'}\cdot \text{x}\cdot \text{y + w'}\cdot \text{x'}\cdot \text{y}\cdot \text{z' + w}\cdot \text{x'}\cdot \text{y}\cdot \text{z'}\\ \text{= }\left(\text{x' + x}\right)\cdot \text{y'}\cdot \text{z}\cdot \left(\text{w' + w}\right)\text{+ w}\cdot \left(\text{x' + x}\right)\cdot \text{y'}\cdot \left(\text{z' + z}\right)\text{ +}\\ \left(\text{z' + z}\right)\cdot \text{w'}\cdot \text{x}\cdot \text{y + w'}\cdot \text{x'}\cdot \text{y}\cdot \text{z' + w}\cdot \text{x'}\cdot \text{y}\cdot \text{z'}\end{array}$

                 $\begin{array}{c}\text{= w}\cdot \text{x}\cdot \text{y'}\cdot \text{z}\text{+ w'}\cdot \text{x}\cdot \text{y'}\cdot \text{z}\text{+ w}\cdot \text{x'}\cdot \text{y'}\cdot \text{z}\text{+ w'}\cdot \text{x'}\cdot \text{y'}\cdot \text{z}\text{+ }\\ \text{ w}\cdot \text{x}\cdot \text{y'}\cdot \text{z + w}\cdot \text{x}\cdot \text{y'}\cdot \text{z' + w}\cdot \text{x'}\cdot \text{y'}\cdot \text{z + w}\cdot \text{x'}\cdot \text{y'}\cdot \text{z' + }\\ \text{ w'}\cdot \text{x}\cdot \text{y}\cdot \text{z + w'}\cdot \text{x}\cdot \text{y}\cdot \text{z'}\text{+ w'}\cdot \text{x'}\cdot \text{y}\cdot \text{z'}\text{+ w}\cdot \text{x'}\cdot \text{y}\cdot \text{z'}\end{array}$

 The K-Map for the given expression is as follows:

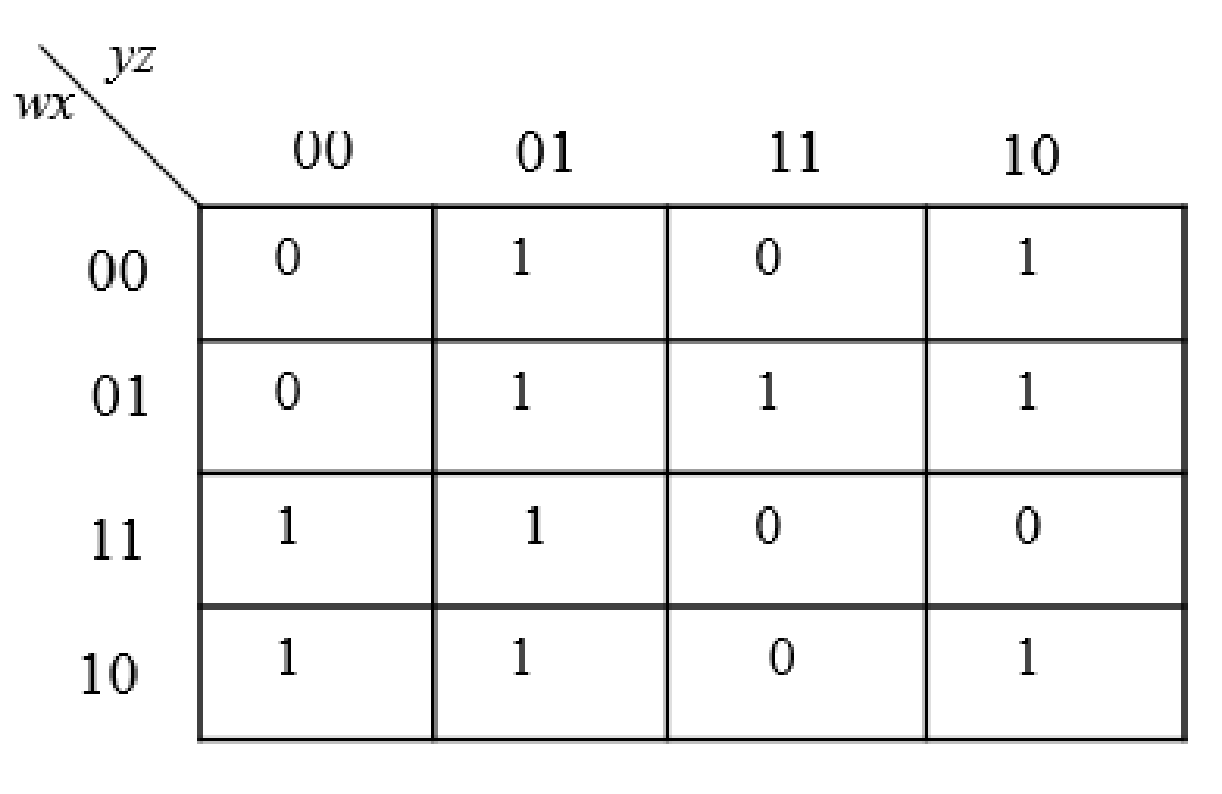
 The following steps are used to obtain the simplified Boolean expressions.

 Step1:

 Then group another possible 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.

  $\begin{array}{c}\text{F = w}\cdot \text{x}\cdot \text{y'}\cdot \text{z'}\text{+ w}\cdot \text{x}\cdot \text{y'}\cdot \text{z}\text{+ w}\cdot \text{x'}\cdot \text{y'}\cdot \text{z'}\text{+ w}\cdot \text{x'}\cdot \text{y'}\cdot \text{z}\\ \text{= w}\cdot \text{x}\cdot \text{y'}\cdot \left(\text{z+z'}\right)\text{ + w}\cdot \text{x'}\cdot \text{y'}\cdot \left(\text{z+z'}\right)\\ =\text{w}\cdot \text{x}\cdot \text{y'}\cdot \left(\text{1}\right)\text{ + w}\cdot \text{x'}\cdot \text{y'}\cdot \left(\text{1}\right)\\ =\text{w}\cdot \text{y'}\cdot \left(\text{x + x'}\right)\end{array}$

           $=\text{w}\cdot \text{y'}$

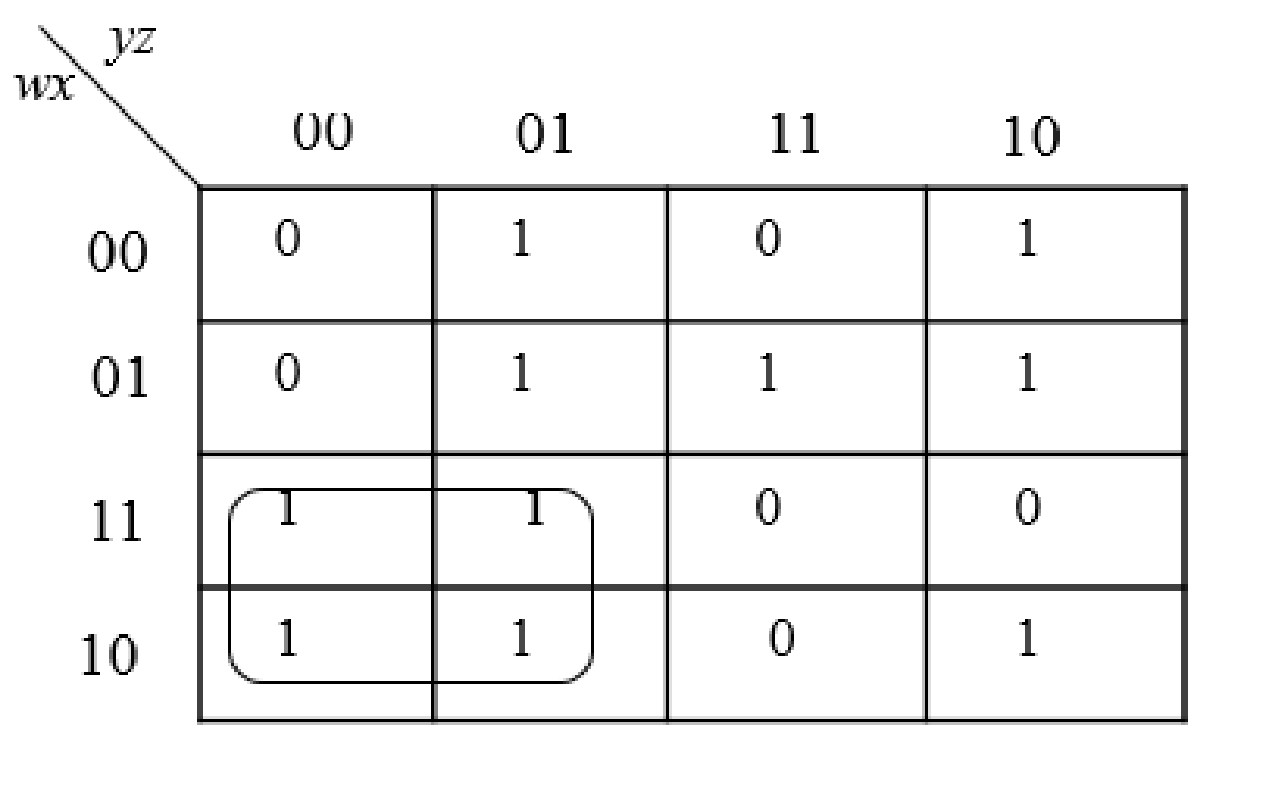
 Step2:

 The group the 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.

     $\begin{array}{c}\text{F = w'}\cdot \text{x'}\cdot \text{y'}\cdot \text{z}\text{+ w'}\cdot \text{x}\cdot \text{y'}\cdot \text{z}\text{+ w}\cdot \text{x}\cdot \text{y'}\cdot \text{z}\text{+ w}\cdot \text{x'}\cdot \text{y'}\cdot \text{z}\\ \text{= w'}\cdot \text{y'}\cdot \text{z}\cdot \left(\text{x+x'}\right)\text{ + w}\cdot \text{y'}\cdot \text{z}\cdot \left(\text{x+x'}\right)\\ =\text{w'}\cdot \text{y'}\cdot \text{z}\cdot \left(\text{1}\right)\text{ + w}\cdot \text{y'}\cdot \text{z}\cdot \left(\text{1}\right)\\ =\text{y'}\cdot \text{z}\cdot \left(\text{w + w'}\right)\end{array}$

                $=\text{ y'}\cdot \text{z}$

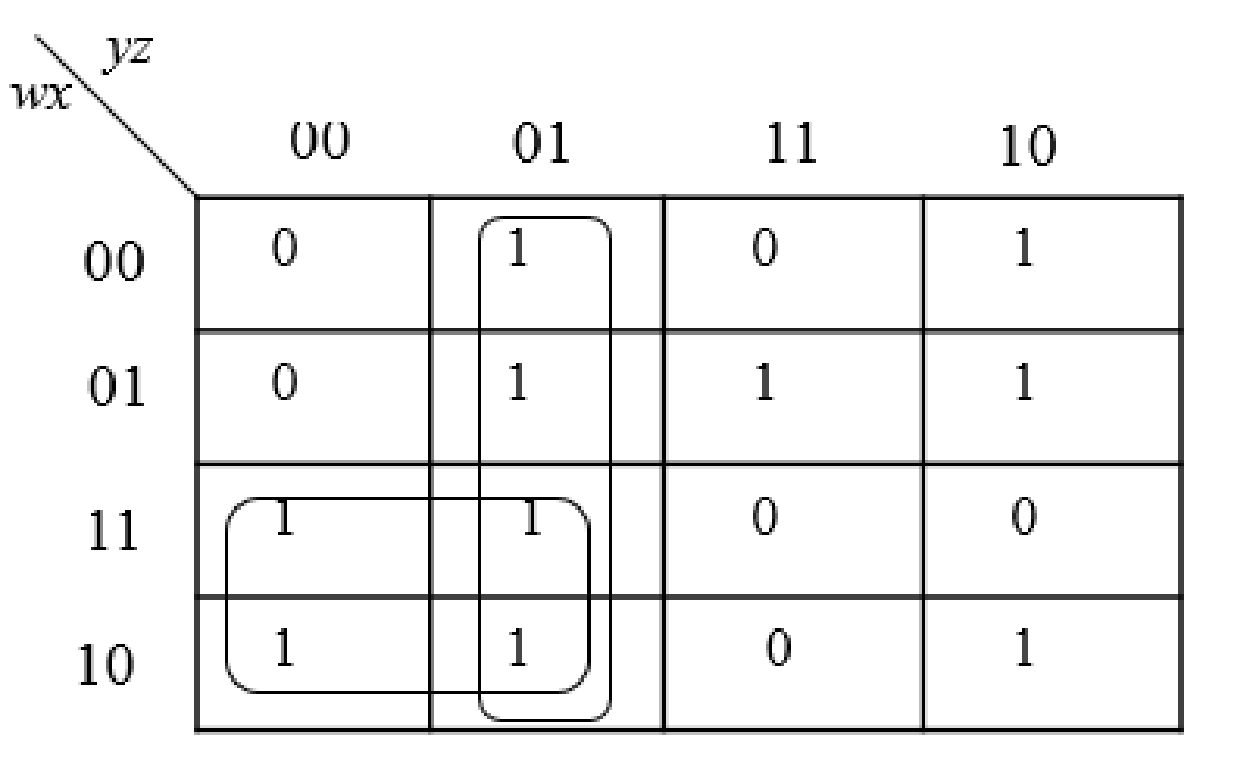
 Step3:

 The group the 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.

     $\begin{array}{c}\text{F = w}\cdot \text{x'}\cdot \text{y'}\cdot \text{z'}\text{+ w}\cdot \text{x'}\cdot \text{y}\cdot \text{z'}\\ \text{= w}\cdot \text{x'}\cdot \text{z'}\cdot \left(\text{y+y'}\right)\\ =\text{w}\cdot \text{x'}\cdot \text{z'}\cdot \left(\text{1}\right)\\ =\text{w}\cdot \text{x'}\cdot \text{z'}\end{array}$

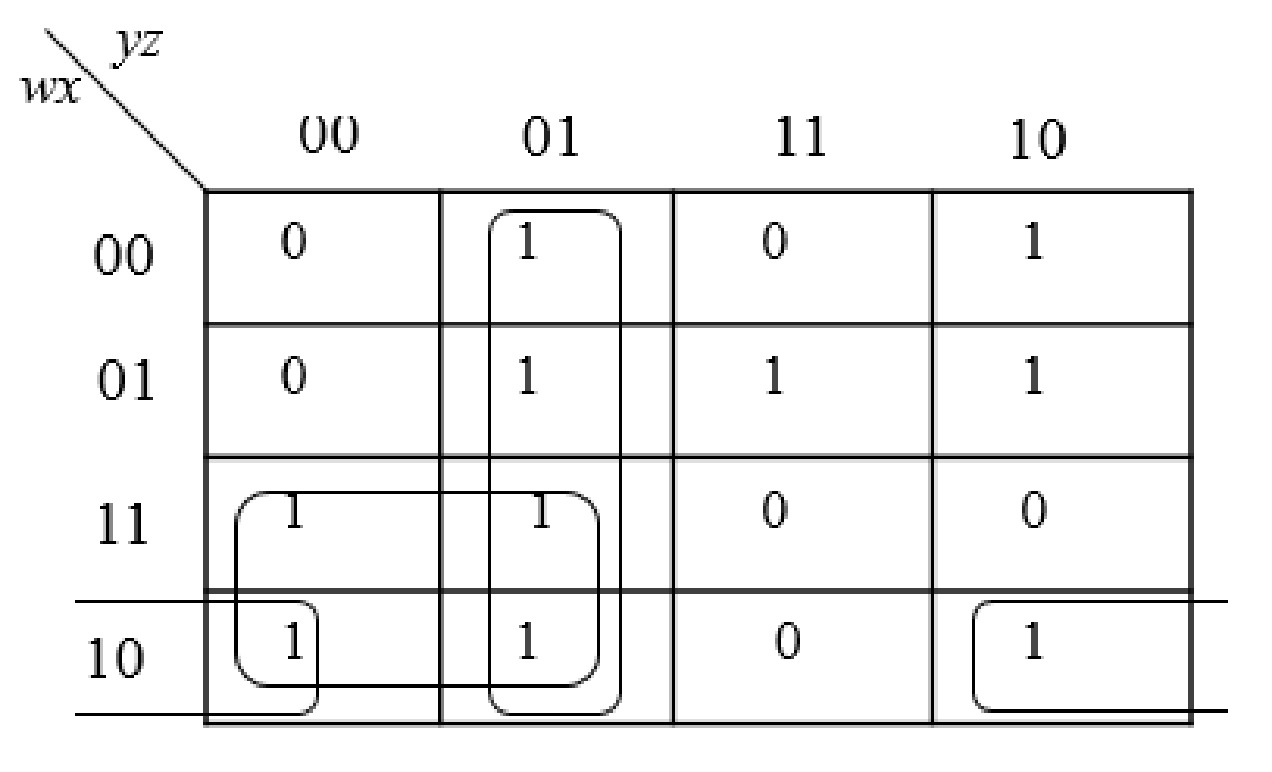
 Step4:

 The group the 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.

     $\begin{array}{c}\text{F = w'}\cdot \text{x'}\cdot \text{y}\cdot \text{z'}\text{+ w'}\cdot \text{x}\cdot \text{y}\cdot \text{z'}\\ \text{= w'}\cdot \text{y}\cdot \text{z'}\cdot \left(\text{x+x'}\right)\\ =\text{w'}\cdot \text{y}\cdot \text{z'}\cdot \left(\text{1}\right)\\ =\text{w'}\cdot \text{y}\cdot \text{z'}\end{array}$

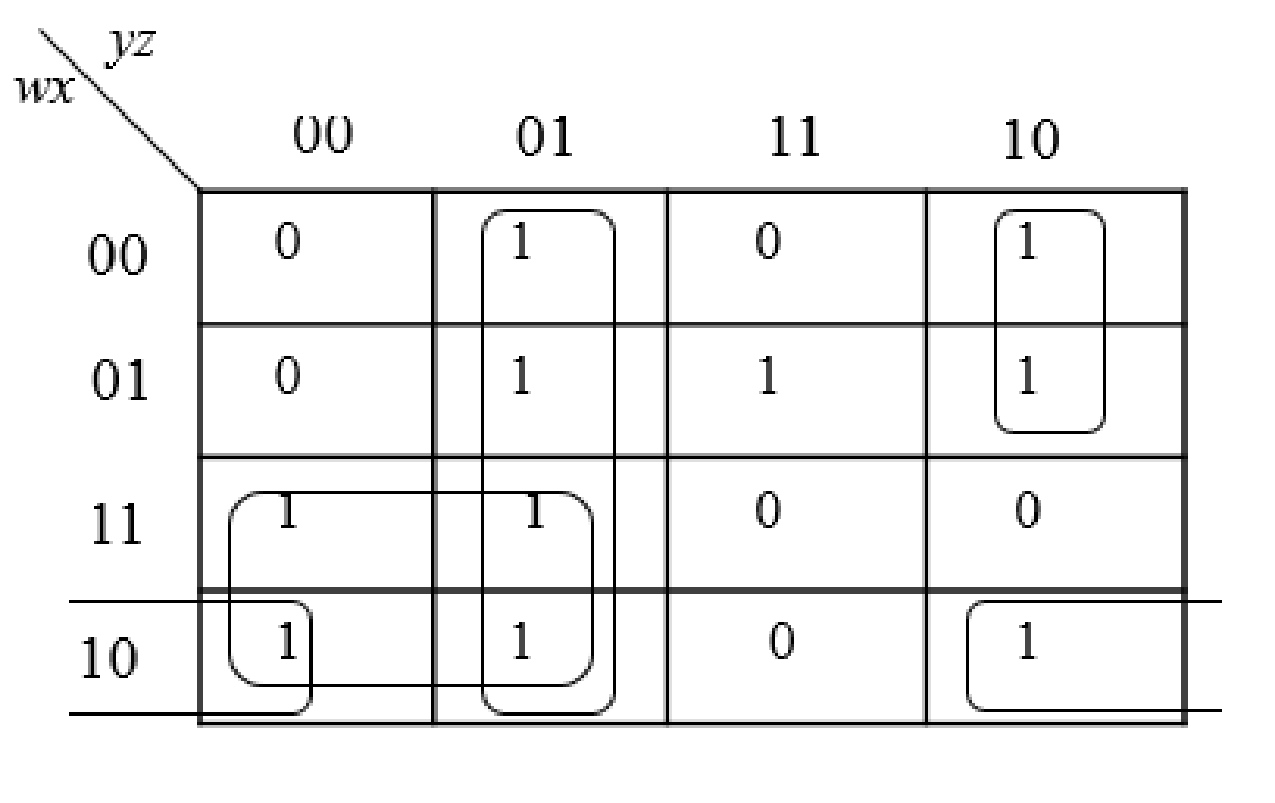
 Step5:

 The group the 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.

     $\begin{array}{c}\text{F = w'}\cdot \text{x}\cdot \text{y}\cdot \text{z}\text{+ w'}\cdot \text{x}\cdot \text{y}\cdot \text{z'}\\ \text{= w'}\cdot \text{x}\cdot \text{y}\cdot \left(\text{z+z'}\right)\\ =\text{w'}\cdot \text{x}\cdot \text{y}\cdot \left(\text{1}\right)\\ =\text{w'}\cdot \text{x}\cdot \text{y}\end{array}$

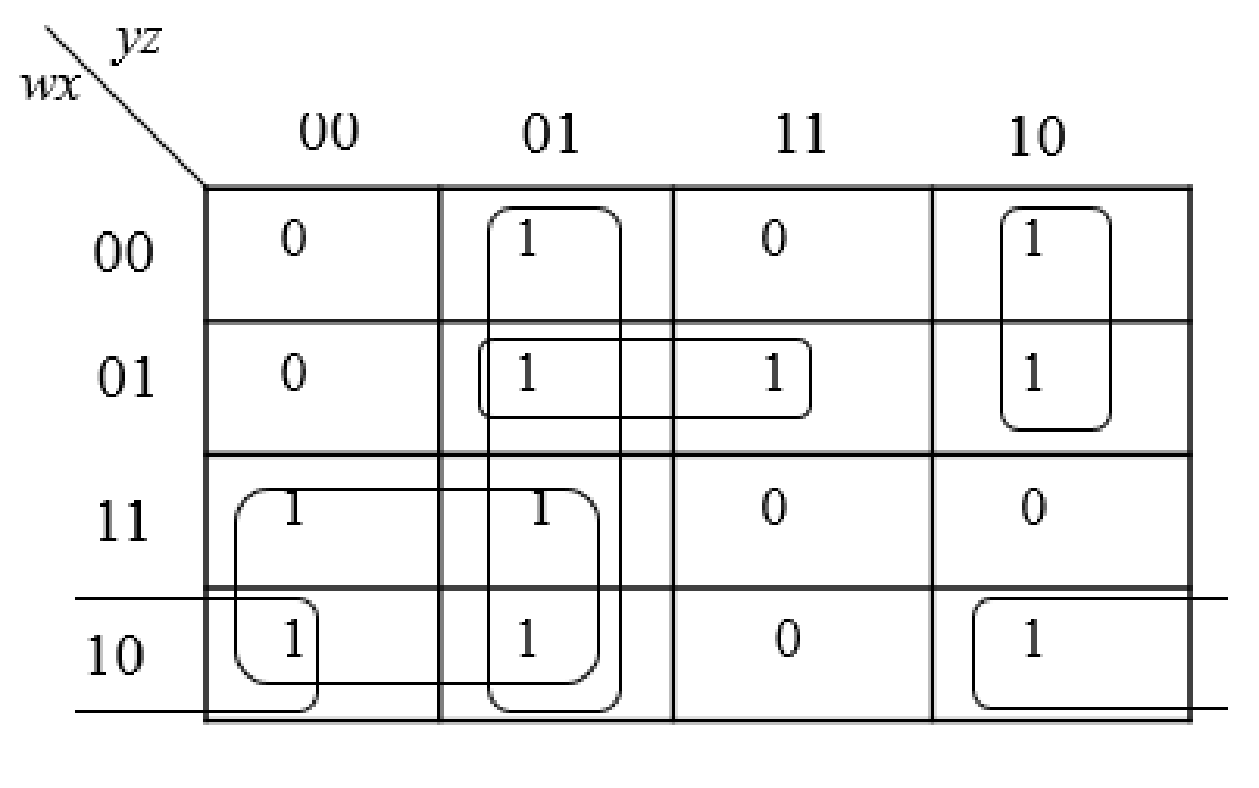
 Step6:

 Group all the expressions

 $\text{F = y'}\cdot \text{z + w'}\cdot \text{y}\cdot \text{z' + w'}\cdot \text{x}\cdot \text{y + w}\cdot \text{y' + w}\cdot \text{x'}\cdot \text{z' }$

 Therefore, the simplified expression is “$F=y\text{'}\cdot z+w\text{'}\cdot y\cdot z\text{'}+w\text{'}\cdot x\cdot y+w\cdot y\text{'}+w\cdot x\text{'}\cdot z\text{'}$”.