Videos
a.
K-Map:
- K-Map stands for Karnaugh Map which is used to reduce the logic functions more easily and quickly.
- It will minimize the Boolean expressions without using Boolean algebra theorems.
- By using K-Map, the Boolean expressions with two to four variables are easily reduced.
Explanation of Solution
Simplification of Boolean expression using K-Map:
Given:
The K-Map for the given expression is as follows:
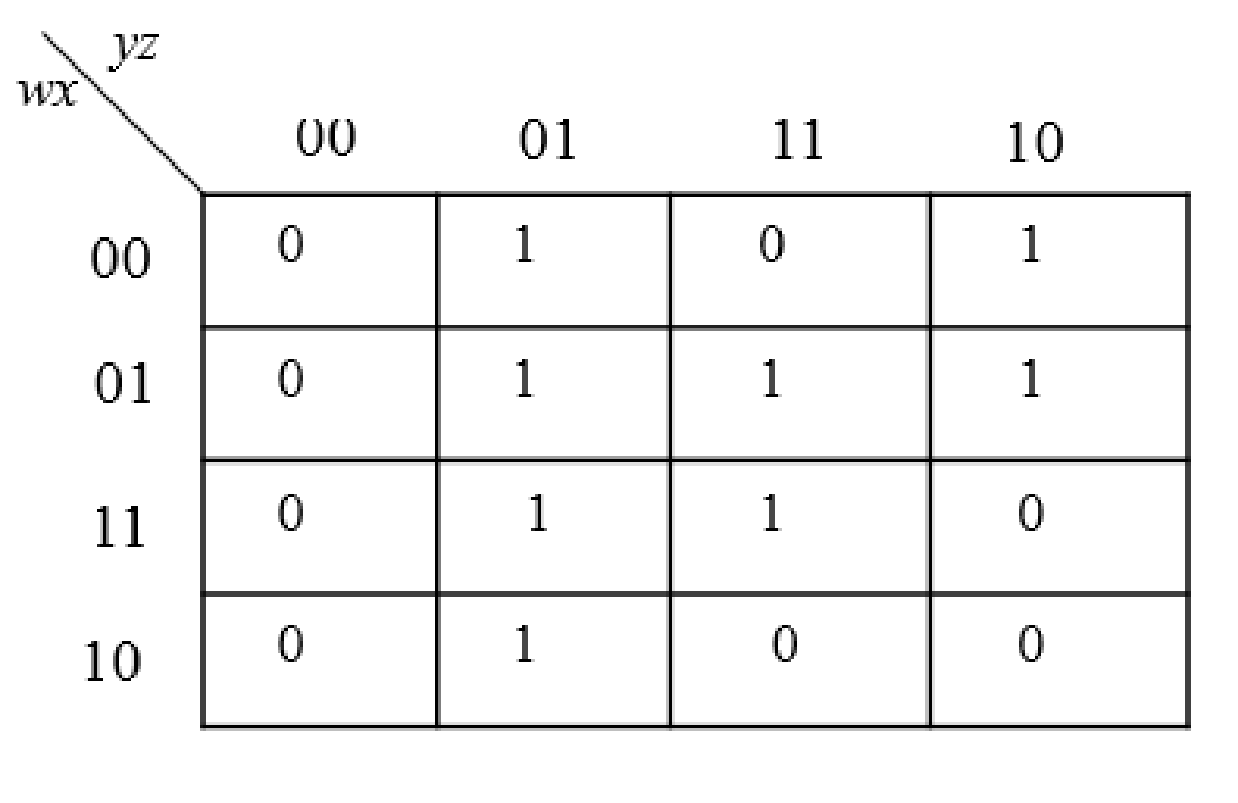
The following steps are used to obtain the simplified Boolean expressions.
Step1:
Then group another possible 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.
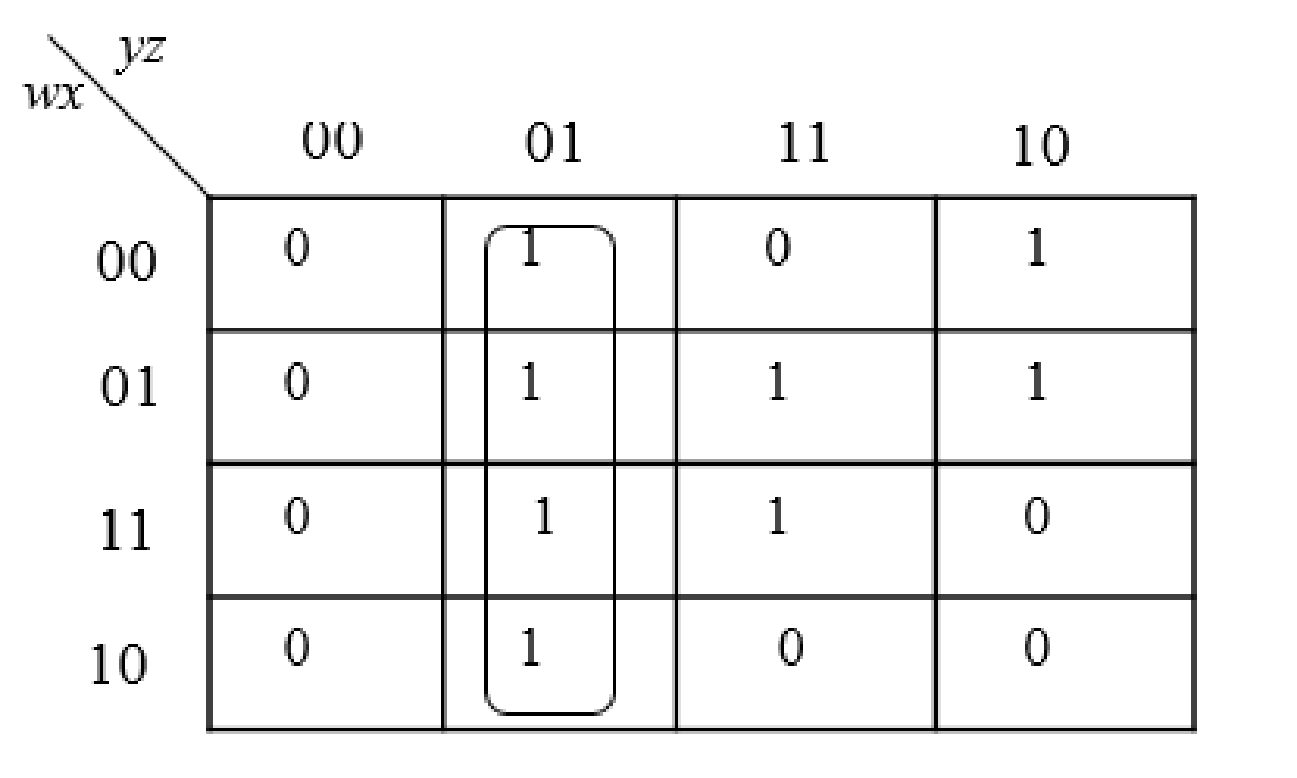
Step2:
The group the 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.
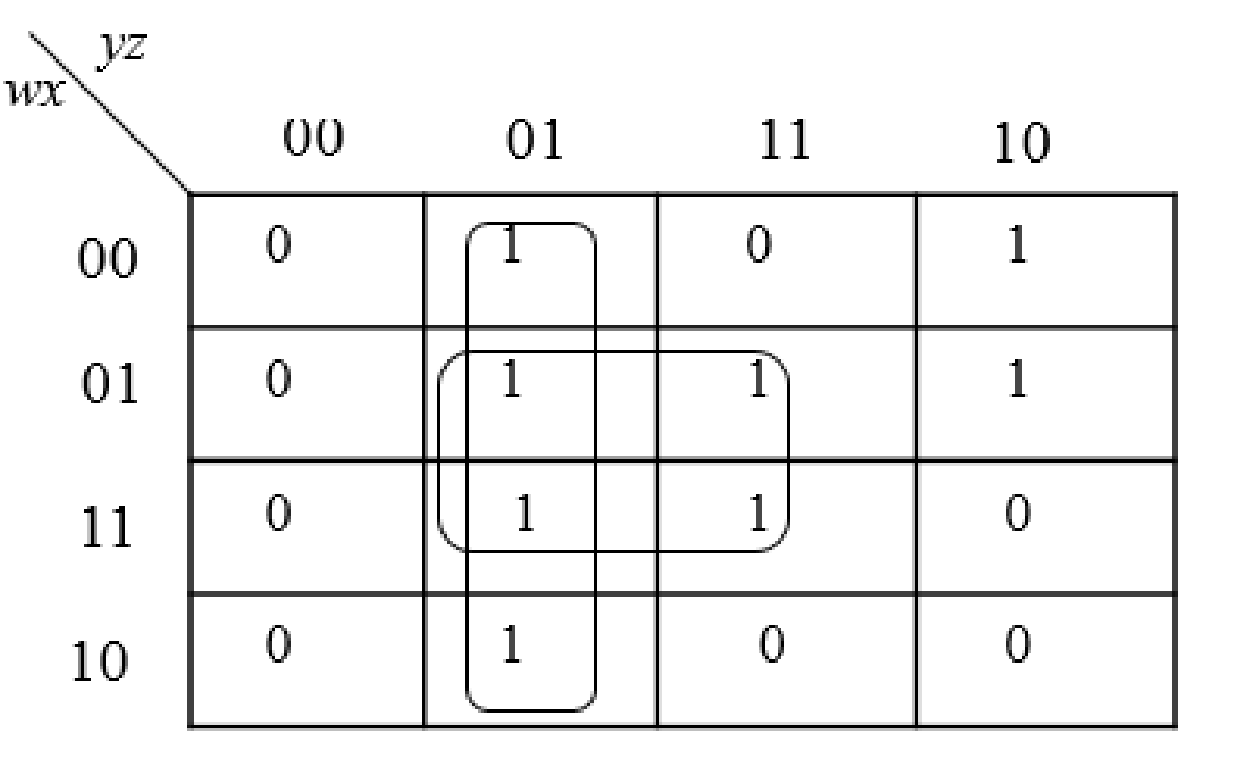
Step3:
The group the 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.
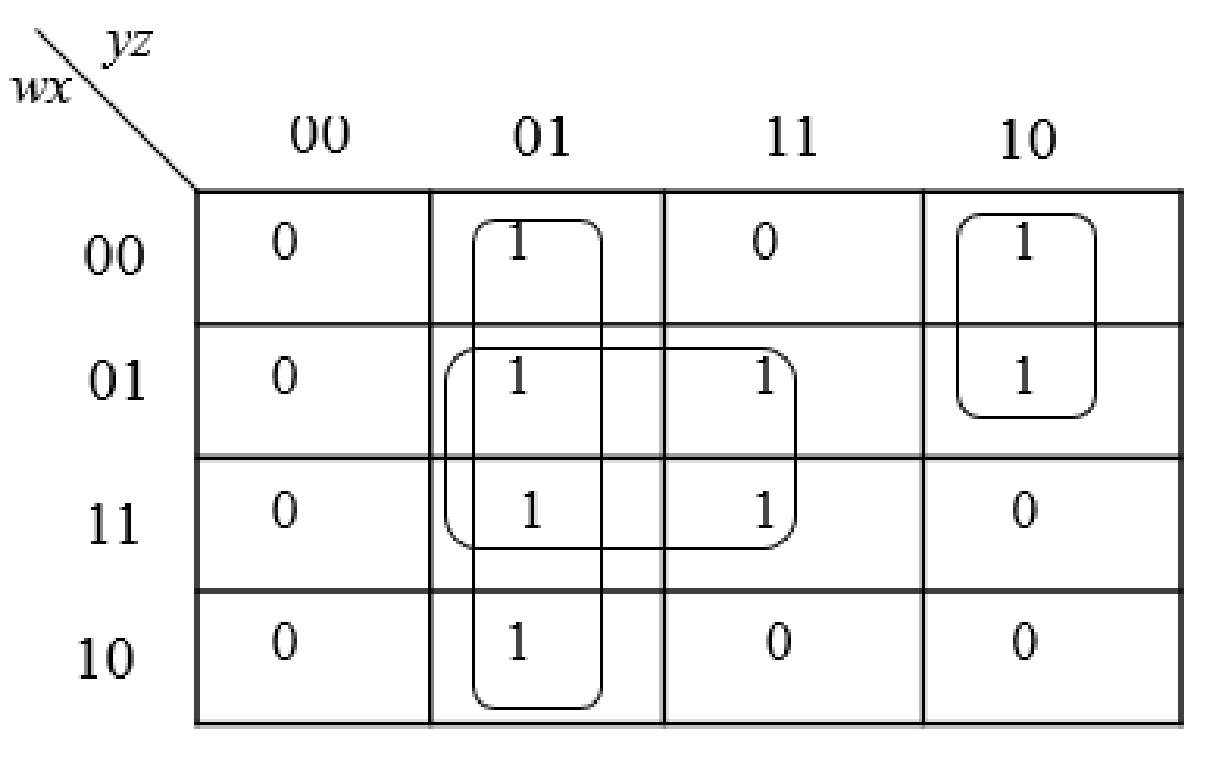
Step4:
Group all the expressions
Therefore, the simplified expression is “
b.
K-Map:
- K-Map stands for Karnaugh Map which is used to reduce the logic functions more easily and quickly.
- It will minimize the Boolean expressions without using Boolean algebra theorems.
- By using K-Map, the Boolean expressions with two to four variables are easily reduced.
Explanation of Solution
Simplification of Boolean expression using K-Map:
Given:
Simplifying the given equation into 4 variable terms as shown below:
The K-Map for the given expression is as follows:
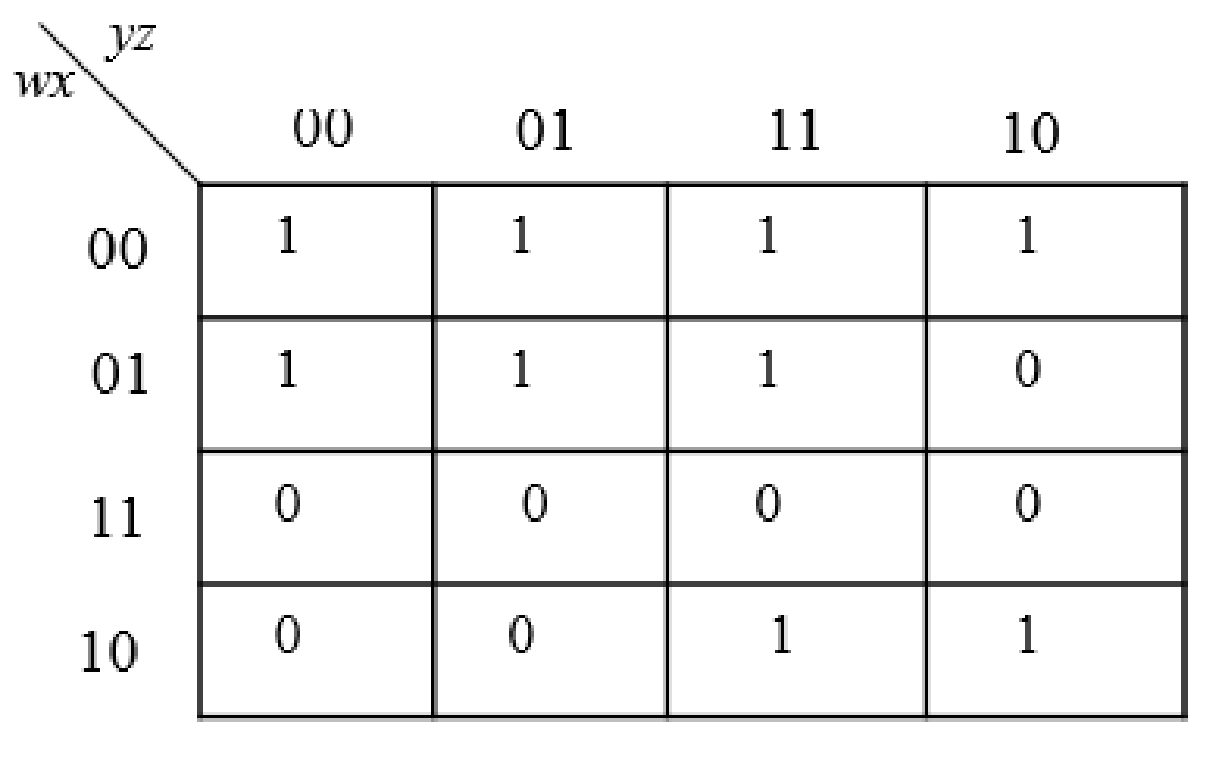
The following steps are used to obtain the simplified Boolean expressions.
Step1:
The group the 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.
Step2:
The group the 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.
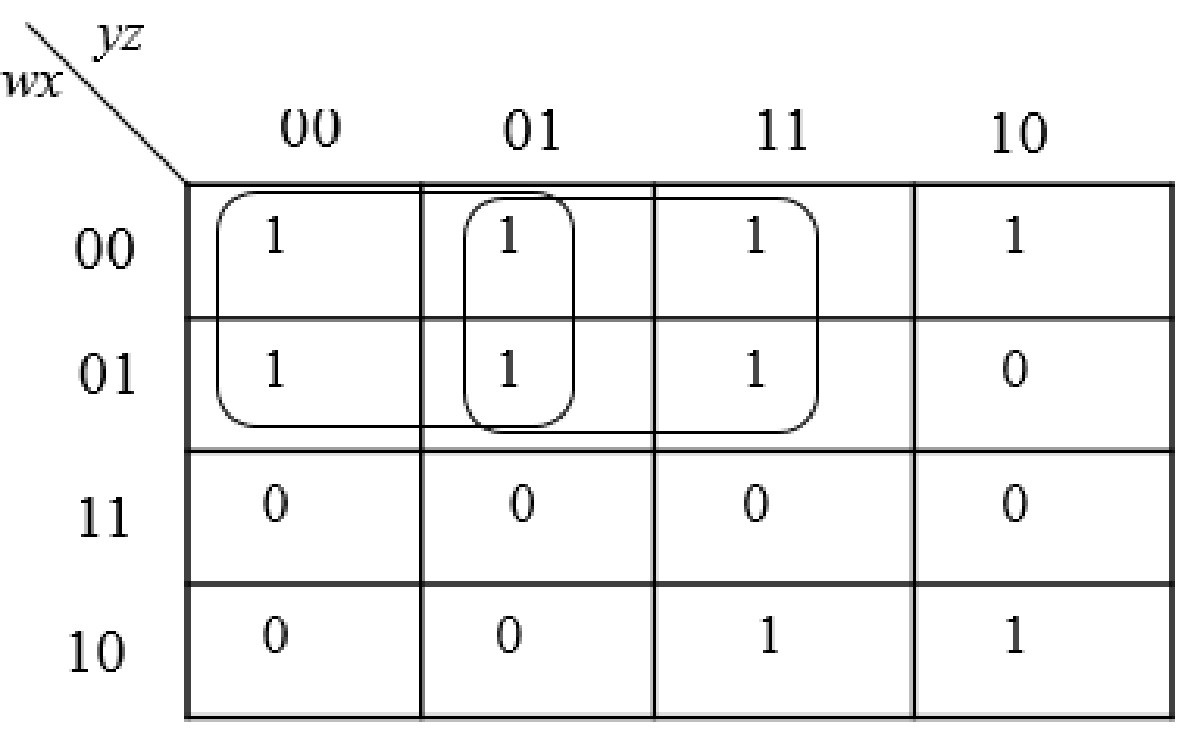
Step3:
The group the 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.
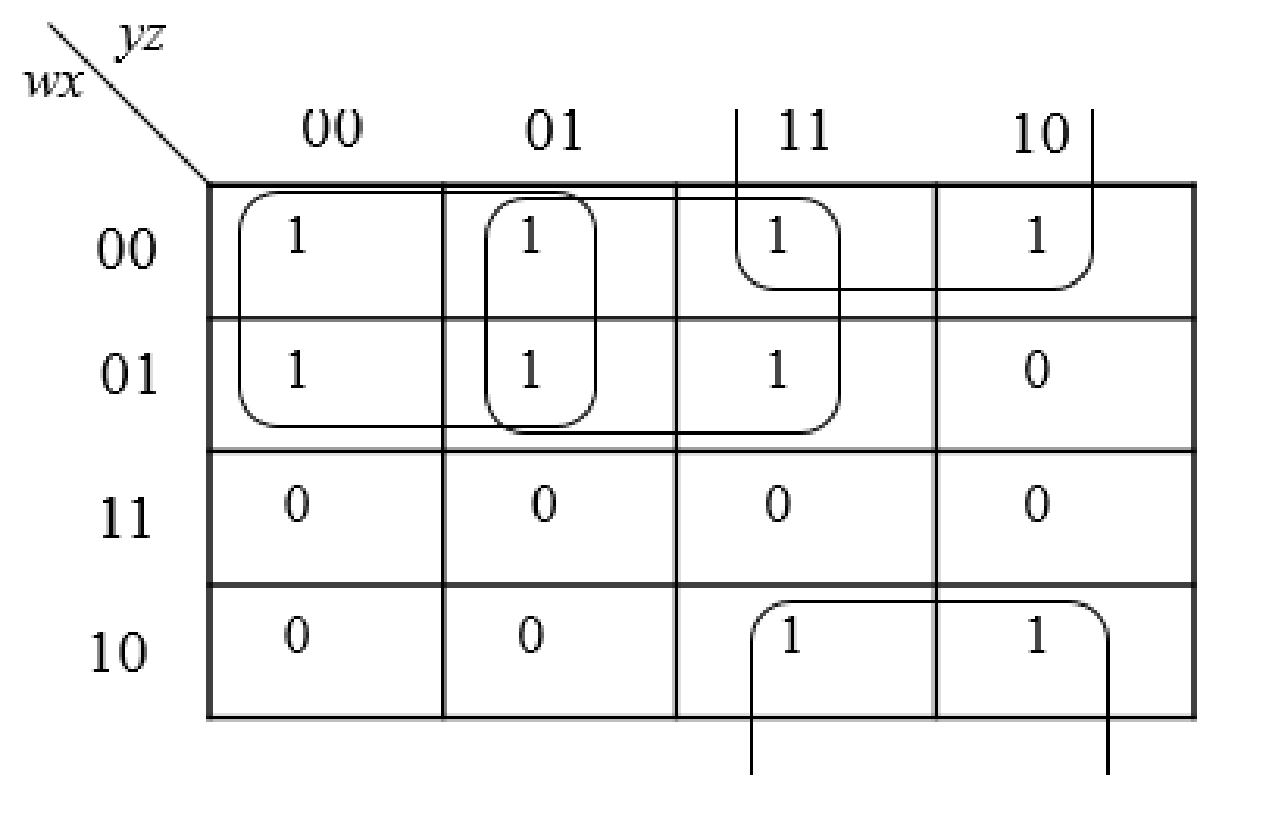
Step4:
Group all the expressions
Therefore, the simplified expression is “
c.
K-Map:
- K-Map stands for Karnaugh Map which is used to reduce the logic functions more easily and quickly.
- It will minimize the Boolean expressions without using Boolean algebra theorems.
- By using K-Map, the Boolean expressions with two to four variables are easily reduced.
Explanation of Solution
Simplification of Boolean expression using K-Map:
Given:
Simplifying the given equation into 4 variable terms as shown below:
The K-Map for the given expression is as follows:
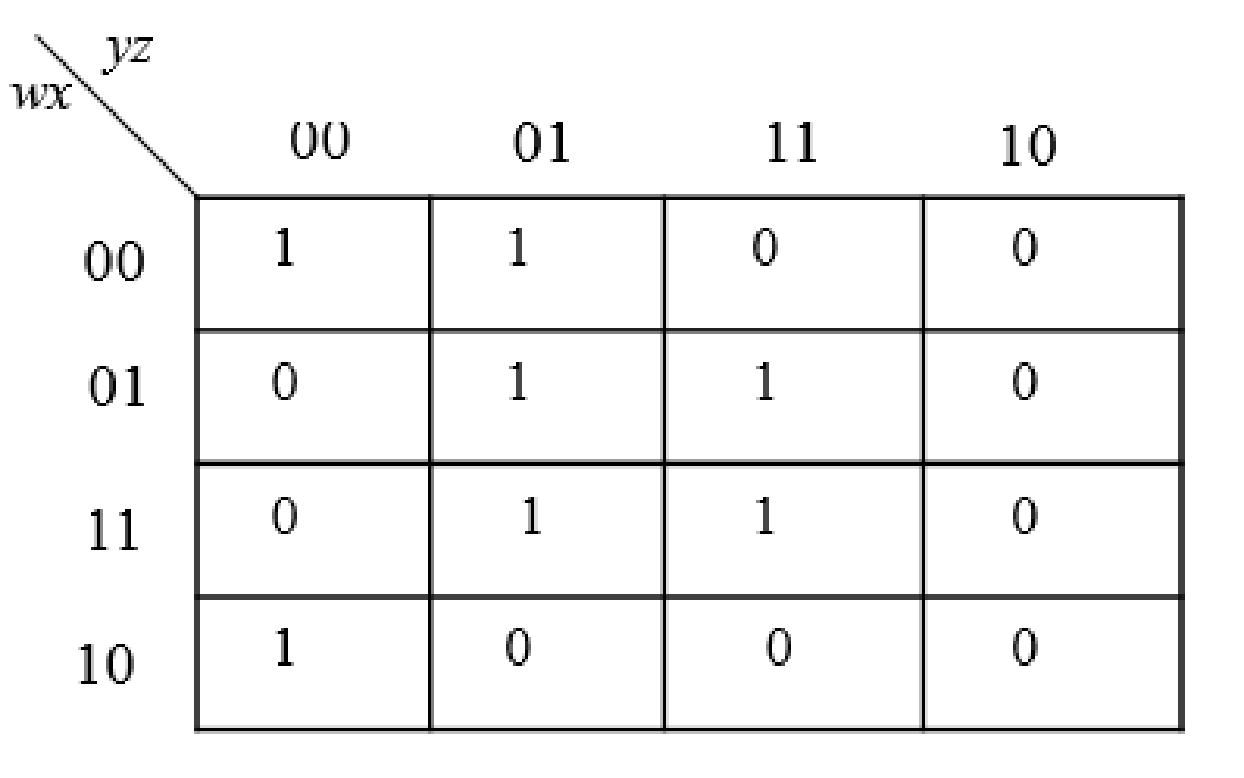
The following steps are used to obtain the simplified Boolean expressions.
Step1:
Then group another possible 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.
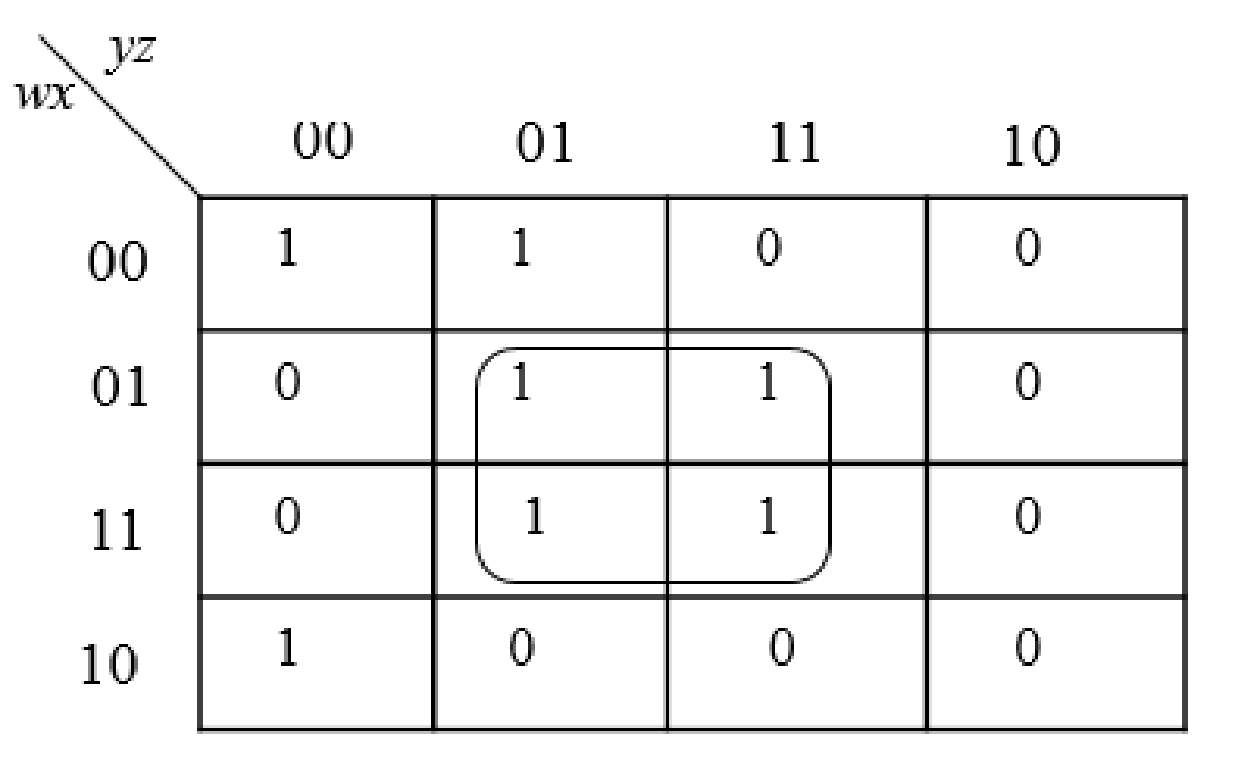
Step2:
The group the 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.
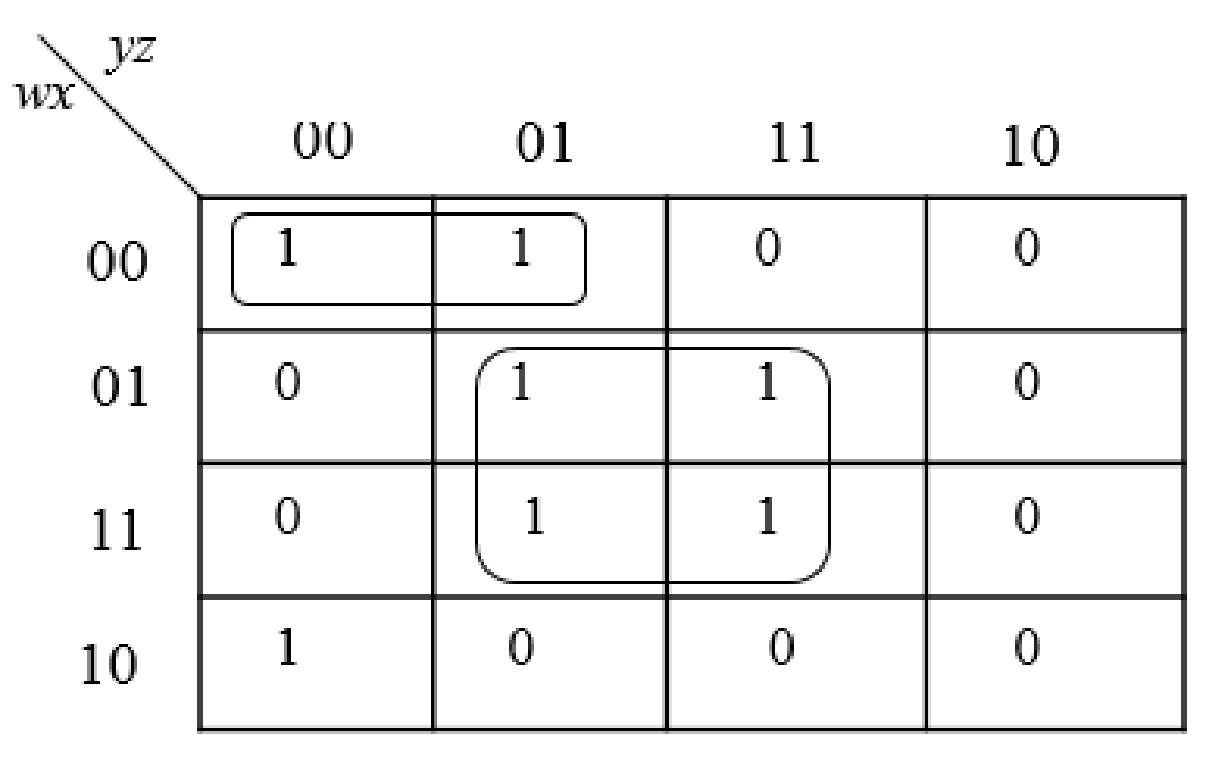
Step3:
The group the 1’s in the table. Then write the Boolean expression according to the mapping. Write 0 term’s as complemented variable like x’ and 1 term’s as it is like x.
Step4:
Group all the expressions
Therefore, the simplified expression is “
Want to see more full solutions like this?
Chapter 3 Solutions
Essentials of Computer Organization and Architecture
- Please answer the homework scenario below and make a JAVA OOP code. You have been hired by GMU to create and manage their course registration portal. Your first task is to develop a program that will create and track different courses in the portal. Each course has the following properties: • a course number ex. IT 106, IT 206, • A course description, ex. Intro to Programming • Total credit hour ex. 3.0, and • current enrollment ex. 30 Each course must have at least a course number and credit hours. The maximum enrollment for each course is 40 students. The current enrollment should be no greater than the maximum enrollment. A course can have a maximum of 4 credit hour. The DDC should calculate the number of seats remaining for the course. Design an object-oriented solution to create a data definition class for the course object. The course class must define all the constructors, mutators with proper validation, accessors, and special purpose methods. The DDC should calculate the…arrow_forwardFor this case study, students will analyze the ethical considerations surrounding artificial intelligence and big data in healthcare, as explored in the case study found in the textbook (pages 34-36) and in the extended version available here There will also be additional articles in this weeks learning module to show both sides of the coin. https://www.delftdesignforvalues.nl/wp-content/uploads/2018/03/Saving-the-life-of-medical-ethics-in-the-age-of-AI-and-Big-Data.pdf Students should refer to the syllabus for specific guidelines regarding length, format, and content requirements. Reflection Questions to Consider: What are the key ethical dilemmas presented in the case? How does AI challenge traditional medical ethics principles such as autonomy, beneficence, and confidentiality? In what ways can responsible innovation help address moral overload in healthcare decision-making? What are the potential risks and benefits of integrating AI-driven decision-making into patient care?…arrow_forwardCan you please solve this. Thanksarrow_forward
- can you solve this pleasearrow_forwardIn the previous homework scenario problem below: You have been hired by TechCo to create and manage their employee training portal. Your first task is to develop a program that will create and track different training sessions in the portal. Each training session has the following properties: • A session ID (e.g., "TECH101", "TECH205") • A session title (e.g., "Machine learning", "Advanced Java Programming") • A total duration in hours (e.g., 5.0, 8.0) • Current number of participants (e.g., 25) Each session must have at least a session ID and a total duration and must met the following requirements: • The maximum participant for each session is 30. • The total duration of a session must not exceed 10 hours. • The current number of participants should never exceed the maximum number of participants. Design an object-oriented solution to create a data definition class(DDC) and an implementation class for the session object. In the DDC, a session class must include: • Constructors to…arrow_forwardIn the previous homework scenario problem below: You have been hired by TechCo to create and manage their employee training portal. Your first task is to develop a program that will create and track different training sessions in the portal. Each training session has the following properties: • A session ID (e.g., "TECH101", "TECH205") • A session title (e.g., "Machine learning", "Advanced Java Programming") • A total duration in hours (e.g., 5.0, 8.0) • Current number of participants (e.g., 25) Each session must have at least a session ID and a total duration and must met the following requirements: • The maximum participant for each session is 30. • The total duration of a session must not exceed 10 hours. • The current number of participants should never exceed the maximum number of participants. Design an object-oriented solution to create a data definition class(DDC) and an implementation class for the session object. In the DDC, a session class must include: • Constructors to…arrow_forward
- Send me the lexer and parserarrow_forwardHere is my code please draw a transition diagram and nfa on paper public class Lexer { private static final char EOF = 0; private static final int BUFFER_SIZE = 10; private Parser yyparser; // parent parser object private java.io.Reader reader; // input stream public int lineno; // line number public int column; // column // Double buffering implementation private char[] buffer1; private char[] buffer2; private boolean usingBuffer1; private int currentPos; private int bufferLength; private boolean endReached; // Keywords private static final String[] keywords = { "int", "print", "if", "else", "while", "void" }; public Lexer(java.io.Reader reader, Parser yyparser) throws Exception { this.reader = reader; this.yyparser = yyparser; this.lineno = 1; this.column = 0; // Initialize double buffering buffer1 = new char[BUFFER_SIZE]; buffer2 = new char[BUFFER_SIZE]; usingBuffer1 = true; currentPos = 0; bufferLength = 0; endReached = false; // Initial buffer fill fillBuffer(); } private…arrow_forwardIf integer x is divisible by 3, can you prove that ceil(x/2) + floor(x/6) = floor(x/2) + ceil(x/6)arrow_forward
- Draw the NFA for thisarrow_forwardWhat are three examples each of closed-ended, open-ended, and range-of-response questions? thank youarrow_forwardCreate 2 charts using this data. One without using wind speed and one including max speed in mph. Write a Report and a short report explaining your visualizations and design decisions. Include the following: Lead Story: Identify the key story or insight based on your visualizations. Shaffer’s 4C Framework: Describe how you applied Shaffer’s 4C principles in the design of your charts. External Data Integration: Explain the second data and how you integrated it with the Halloween dataset. Compare the two datasets. Attach screenshots of the two charts (Bar graph or Line graph) The Shaffer 4 C’s of Data Visualization Clear - easily seen; sharply defined• who's the audience? what's the message? clarity more important than aestheticsClean - thorough; complete; unadulterated, labels, axis, gridlines, formatting, right chart type, colorchoice, etc.Concise - brief but comprehensive. not minimalist but not verboseCaptivating - to attract and hold by beauty or excellence does it capture…arrow_forward
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education