Chapter 29, Problem 7P

(a)

To determine

The magnitude and direction of magnetic field at point $A$.

Answer to Problem 7P

The magnitude of magnetic field at point $A$ is $53.3\text{}\text{μT}$ and direction is toward the bottom of page.

Explanation of Solution

Given Info: The current flowing through the conductor is $2.00\text{A}$, distance between corner of square to centre of square is $1.00\text{cm}$.

Diagram of three parallel conductor having current of magnitude $I$ is given below.

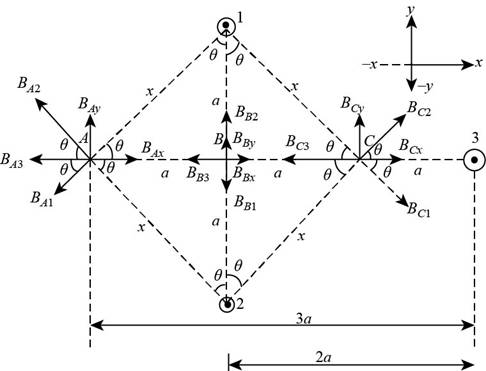
Figure (1)

Formula to calculate side of the square is,

$\begin{array}{c}x=\sqrt{a^2+a^2}\\ =\sqrt{2}a\end{array}$

Formula to calculate angle $\theta$

$\begin{array}{c}\theta ={\tan }^{-1}\left(\frac{a}{a}\right)\\ ={\tan }^{-1}\left(1\right)\\ ={45}^{°}\end{array}$

Formula to calculate magnetic field at point $A$ due to conductor 1,

$B_A{}_{{}_1}=\frac{{\mu }_{o}I}{2\pi r}$

Here

$I$ is current flowing through conductor.

$r$ is distance of the the point $A$ from conductors 1.

Substitute $\sqrt{2}a$ for $r\text{or}x$ in above equation

$\begin{array}{c}{B}_A{}_{{}_1}=\frac{{\mu }_{o}I}{2\pi \left(\sqrt{2}a\right)}\\ =\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}\end{array}$

Formula to calculate magnetic field at point $A$ due to conductor 2

$B_{A_2}=\frac{{\mu }_{o}I}{2\pi r}$

Here

$I$ is current flowing through conductor.

$r$ is distance of the the point $A$ from conductors.2

Substitute $\sqrt{2}a$ for $r\text{or}x$ in above equation

$\begin{array}{c}{B}_A{}_{{}_2}=\frac{{\mu }_{o}I}{2\pi \left(\sqrt{2}a\right)}\\ =\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}\end{array}$

Formula to calculate magnetic field at point $A$ due to conductor 3,

$B_{A_3}=\frac{{\mu }_{o}I}{2\pi r}$

Here

$I$ is current flowing through conductor.

$r$ is distance of the the point $A$ from conductors 3.

Substitute $3a$ for $r\text{or}x$ in above equation

$\begin{array}{c}{B}_A{}_{{}_3}=\frac{{\mu }_{o}I}{2\pi \left(3a\right)}\\ =\frac{{\mu }_{o}I}{6\pi a}\end{array}$

Write the expression to calculate magnetic field at point $A$ due to conductors by summing in x-direction.

$\begin{array}{c}{\displaystyle \sum B_x=0}\\ B_{A_x}-B_{A_3}+B_{A_2}\cos \theta +B_{A_1}\cos \theta =0\\ B_{A_x}=B_{A_3}+B_{A_2}\cos \theta +B_{A_1}\cos \theta \end{array}$ (1)

Here,

$B_{A_1}$ is magnetic field at $A$ due to conductor 1.

$B_{A_2}$ is magnetic field at $A$ due to conductor 2.

$B_{A_3}$ is magnetic field at $A$ due to conductor 3.

Substitute $\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}$ for $B_{A_{\text{1}}}\text{and}{B}_{A_{\text{2}}}$ and $\frac{{\mu }_{o}I}{6\pi a}$ for $B_{A_3}$ and ${45}^{°}$ for $\theta$ in equation (1).

$\begin{array}{c}{B}_{A_x}=\frac{{\mu }_{o}I}{6\pi a}+\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}\cos {45}^{°}+\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}\cos {45}^{°}\\ =\frac{{\mu }_{o}I}{6\pi a}+\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}\left(\frac{1}{\sqrt{2}}\right)+\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}\left(\frac{1}{\sqrt{2}}\right)\\ =\frac{{\mu }_{o}I}{6\pi a}+\frac{{\mu }_{o}I}{4\pi a}+\frac{{\mu }_{o}I}{4\pi a}\\ =\frac{2}{3}\frac{{\mu }_{o}I}{\pi a}\end{array}$

substitute $4\pi \times {10}^{-7}\raisebox{1ex}{$\text{Tm}$}\!\left/ \!\raisebox{-1ex}{$\text{A}$}\right.$ for ${\mu }_o$, $2.00\text{A}$ for $I$ and $1.00\text{cm}$ for $a$ in above equation.

$\begin{array}{c}{B}_{A_x}=\frac{2}{3}\left(\frac{\left(4\pi \times {10}^{-7}\raisebox{1ex}{$\text{Tm}$}\!\left/ \!\raisebox{-1ex}{$\text{A}$}\right.\right)\left(2.00\text{A}\right)}{\pi \left(1.00\text{cm}\right)}\right)\\ =\frac{2}{3}\left(\frac{\left(4\pi \times {10}^{-7}\raisebox{1ex}{$\text{Tm}$}\!\left/ \!\raisebox{-1ex}{$\text{A}$}\right.\right)\left(2.00\text{A}\right)}{\pi \left(1.00\text{cm}\frac{{10}^{-2}\text{m}}{1\text{cm}}\right)}\right)\\ =53.3\times {10}^{-6}\text{T}\\ =53.3\text{μT}\end{array}$

Write the expression to calculate y-component of magnetic field at $A$ by summing all in y-direction.

$\begin{array}{c}{\displaystyle \sum B_Y=0}\\ B_{A_y}-B_{A_1}\sin {45}^{°}+B_{A_2}\sin {45}^{°}=0\end{array}$

Substitute $\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}$ for $B_{A_1}$ and $\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}$ for $B_{A_2}$.

$\begin{array}{c}{B}_{A_y}-\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}\sin 45+\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}\cos 45=0\\ B_{A_y}=0\end{array}$

Formula to calculate net magnetic field at point $A$,

$B_A=\sqrt{B_{A_x}{}^2+B_{A_y}{}^2}$ (2)

Substitute $53.3\text{μT}$ for $B_{A_x}$ and $0$ for $B_{A_y}$ in above equation.

$\begin{array}{c}{B}_A=\sqrt{{\left(53.3\text{μT}\right)}^2+0}\\ =53.3\text{μT}\end{array}$

Hence, magnetic field at point $A$ is $53.3\text{μT}$ and direction is toward the bottom of page from rule of right hand with grasp figure where thumb shows direction of current and grasp figure shows plane of magnetic field.

Conclusion:

Therefore magnetic field at point $A$ is $53.3\text{μT}$ and direction is toward the bottom of page from rule of right hand with grasp figure where thumb shows direction of current and grasp figure shows plane of magnetic field.

(b)

To determine

magnitude and direction of magnetic field at point $B$.

Answer to Problem 7P

magnitude of magnetic field at point $B$  is $20.0\text{}\text{μT}$ and direction is toward the bottom of page.

Explanation of Solution

Formula to calculate magnetic field at point $B$ due to conductor 1,

$B_B{}_{{}_1}=\frac{{\mu }_{o}I}{2\pi r}$

Here

$I$ is current flowing through conductor.

$r$ is distance of the the point $B$ from conductors 1.

Substitute $a$ for $r\text{or}x$ in above equation

$\begin{array}{c}{B}_B{}_{{}_1}=\frac{{\mu }_{o}I}{2\pi \left(a\right)}\\ =\frac{{\mu }_{o}I}{2\pi a}\end{array}$

Formula to calculate magnetic field at point $B$ due to conductor 2

$B_{B_2}=\frac{{\mu }_{o}I}{2\pi r}$

Here

$I$ is current flowing through conductor.

$r$ is distance of the the point $B$ from conductors.2

Substitute $a$ for $r\text{or}x$ in above equation

$\begin{array}{c}{B}_B{}_{{}_2}=\frac{{\mu }_{o}I}{2\pi \left(a\right)}\\ =\frac{{\mu }_{o}I}{2\pi a}\end{array}$

Formula to calculate magnetic field at point $B$ due to conductor 3,

$B_{B_3}=\frac{{\mu }_{o}I}{2\pi r}$

Here

$I$ is current flowing through conductor.

$r$ is distance of the the point $B$ from conductors 3.

Substitute $2a$ for $r\text{or}x$ in above equation

$\begin{array}{c}{B}_B{}_{{}_3}=\frac{{\mu }_{o}I}{2\pi \left(2a\right)}\\ =\frac{{\mu }_{o}I}{4\pi a}\end{array}$

Write the expression to calculate magnetic field at point $B$ due to conductors by summing in x-direction.

$\begin{array}{c}{\displaystyle \sum B_x=0}\\ B_{B_x}-B_{B_3}=0\\ B_{B_x}=B_{B_3}\end{array}$ (3)

Here,

$B_{B_1}$ is magnetic field at $B$ due to conductor 1.

$B_{B_2}$ is magnetic field at $B$ due to conductor 2.

$B_{B_3}$ is magnetic field at $B$ due to conductor 3.

Substitute $\frac{{\mu }_{o}I}{4\pi a}$ for $B_{B_3}$ in equation (3).

$B_{B_x}=\frac{{\mu }_{o}I}{4\pi a}$

substitute $4\pi \times {10}^{-7}\raisebox{1ex}{$\text{Tm}$}\!\left/ \!\raisebox{-1ex}{$\text{A}$}\right.$ for ${\mu }_o$, $2.00\text{A}$ for $I$ and $1.00\text{cm}$ for $a$ in above equation.

$\begin{array}{c}{B}_{B_x}=\left(\frac{\left(4\pi \times {10}^{-7}\raisebox{1ex}{$\text{Tm}$}\!\left/ \!\raisebox{-1ex}{$\text{A}$}\right.\right)\left(2.00\text{A}\right)}{4\pi \left(1.00\text{cm}\right)}\right)\\ =\left(\frac{\left(4\pi \times {10}^{-7}\raisebox{1ex}{$\text{Tm}$}\!\left/ \!\raisebox{-1ex}{$\text{A}$}\right.\right)\left(2.00\text{A}\right)}{4\pi \left(1.00\text{cm}\frac{{10}^{-2}\text{m}}{1\text{cm}}\right)}\right)\\ =20\times {10}^{-6}\text{T}\\ \text{=20}\text{μT}\end{array}$

Write the expression to calculate y-component of magnetic field at $B$ by summing all in y-direction.

$\begin{array}{c}{\displaystyle \sum B_Y=0}\\ B_{B_y}-B_{{\text{B}}_{\text{1}}}+B_{{\text{B}}_{\text{2}}}=0\end{array}$

Substitute $\frac{{\mu }_{o}I}{2\pi a}$ for $B_{{\text{B}}_{\text{2}}}$ and $\frac{{\mu }_{o}I}{2\pi a}$ for $B_{{\text{B}}_{\text{1}}}$ in above equation.

$\begin{array}{c}{B}_{B_y}-\frac{{\mu }_{o}I}{2\pi a}+\frac{{\mu }_{o}I}{2\pi a}=0\\ B_{B_y}=0\end{array}$

Formula to calculate net magnetic field at point $A$,

$B_B=\sqrt{B_{B_x}{}^2+B_{B_y}{}^2}$ (II)

Substitute $53.3\text{μT}$ for $B_{A_x}$ and $0$ for $B_{A_y}$ in above equation.

$\begin{array}{c}{B}_B=\sqrt{{\left(20.0\text{μT}\right)}^2+0}\\ =20.0\text{μT}\end{array}$

Hence, magnetic field at point $B$ is $20.0\text{μT}$ and direction is toward the bottom of page from rule of right hand with grasp figure where thumb shows direction of current and grasp figure shows plane of magnetic field.

Conclusion:

Therefore magnetic field at point $B$ is $20.0\text{μT}$ and direction is toward the bottom of page from rule of right hand with grasp figure where thumb shows direction of current and grasp figure shows plane of magnetic field.

(c)

To determine

magnitude and direction of magnetic field at point $C$.

Answer to Problem 7P

magnitude of magnetic field at point $C$ is $0$.

Explanation of Solution

Formula to calculate magnetic field at point $C$ due to conductor 1,

$B_C{}_{{}_1}=\frac{{\mu }_{o}I}{2\pi r}$

Here

$I$ is current flowing through conductor.

$r$ is distance of the the point $C$ from conductors 1.

Substitute $\sqrt{2}a$ for $r\text{or}x$ in above equation

$\begin{array}{c}{B}_C{}_{{}_1}=\frac{{\mu }_{o}I}{2\pi \left(\sqrt{2}a\right)}\\ =\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}\end{array}$

Formula to calculate magnetic field at point $C$ due to conductor 2

$B_{C_2}=\frac{{\mu }_{o}I}{2\pi r}$

Here

$I$ is current flowing through conductor.

$r$ is distance of the the point $C$ from conductors.2

Substitute $\sqrt{2}a$ for $r\text{or}x$ in above equation

$\begin{array}{c}{B}_C{}_{{}_2}=\frac{{\mu }_{o}I}{2\pi \left(\sqrt{2}a\right)}\\ =\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}\end{array}$

Formula to calculate magnetic field at point $C$ due to conductor 3,

$B_{C_3}=\frac{{\mu }_{o}I}{2\pi r}$

Here

$I$ is current flowing through conductor.

$r$ is distance of the the point $C$ from conductors 3.

Substitute $a$ for $r\text{or}x$ in above equation

$\begin{array}{c}{B}_C{}_{{}_3}=\frac{{\mu }_{o}I}{2\pi \left(a\right)}\\ =\frac{{\mu }_{o}I}{2\pi a}\end{array}$

Write the expression to calculate magnetic field at point $A$ due to conductors by summing in x-direction.

$\begin{array}{c}{\displaystyle \sum B_x=0}\\ B_{C_x}-B_{C_3}+B_{C_2}\cos \theta +B_{C_1}\cos \theta =0\\ B_{C_x}=-B_{C_3}+B_{C_2}\cos \theta +B_{C_1}\cos \theta \end{array}$ (I)

Here,

$B_{C_1}$ is magnetic field at $C$ due to conductor 1.

$B_{C_2}$ is magnetic field at $C$ due to conductor 2.

$B_{C_3}$ is magnetic field at $C$ due to conductor 3.

Substitute $\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}$ for $B_{C_{\text{1}}}\text{and}{B}_{C_{\text{2}}}$ and $\frac{{\mu }_{o}I}{2\pi a}$ for $B_{C_3}$ in equation (I) and ${45}^{°}$ for $\theta$ in equation (I).

$\begin{array}{c}{B}_{C_x}=-\frac{{\mu }_{o}I}{2\pi a}+\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}\cos {45}^{°}+\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}\cos {45}^{°}\\ =-\frac{{\mu }_{o}I}{2\pi a}+\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}\left(\frac{1}{\sqrt{2}}\right)+\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}\left(\frac{1}{\sqrt{2}}\right)\\ =-\frac{{\mu }_{o}I}{2\pi a}+\frac{{\mu }_{o}I}{4\pi a}+\frac{{\mu }_{o}I}{4\pi a}\\ =0\end{array}$

Write the expression to calculate y-component of magnetic field at $C$ by summing all in y-direction.

$\begin{array}{c}{\displaystyle \sum B_Y=0}\\ B_{C_y}-B_{C_1}\sin {45}^{°}+B_{C_2}\sin {45}^{°}=0\end{array}$

Substitute $\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}$ for $B_{C_1}$ and $\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}$ for $B_{C_2}$.

$\begin{array}{c}{B}_{C_y}-\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}\sin 45+\frac{{\mu }_{o}I}{2\sqrt{2}\pi a}\cos 45=0\\ B_{C_y}=0\end{array}$

Formula to calculate net magnetic field at point $C$,

$B_C=\sqrt{B_{C_x}{}^2+B_{C_y}{}^2}$ (II)

Substitute $0\text{μT}$ for $B_{c_x}$ and $0$ for $B_{C_y}$ in above equation.

$\begin{array}{c}{B}_C=\sqrt{0+0}\\ =0\end{array}$

Hence, magnetic field at point $A$ is $0$.

Conclusion:

Therefore magnetic field at point $A$ is $0$.