University Physics with Modern Physics (14th Edition)
14th Edition
ISBN: 9780321973610
Author: Hugh D. Young, Roger A. Freedman
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 28, Problem 28.67P
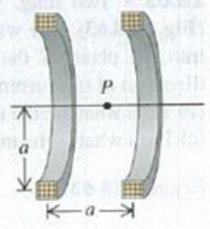
CALC Helmholtz Coils. Figure P28.67 is a sectional view of two circular coils with radius a. each wound with N turns of wire carrying a current I, circulating in the same direction in both coils. The coils are separated by a distance a equal to their radii. In this configuration the coils are called Helmholtz coils; they produce a very uniform magnetic field in the region between them, (a) Derive the expression for the magnitude B of the magnetic field at a point on the axis a distance x to the right of point P, which is midway between the coils, (b) Graph B versus x for x = 0 to x = a/2. Compare this graph to one for the magnetic field due to the right-hand coil alone, (c) From part (a), obtain an expression for the magnitude of the magnetic field at point P. (d) Calculate the magnitude of the magnetic field at P if N = 300 turns, I = 6.00 A, and a = 8.00 cm. (e) Calculate dB/dx and d2B/dx2 at P(x = 0). Discuss how your results show that the field is very uniform in the vicinity of P.
Figure P28.67
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Please solve and answer the problem correctly please. Be sure to give explanations on each step and write neatly please. Thank you!!
In the figures, the masses are hung from an elevator ceiling. Assume the velocity of the elevator is constant. Find the tensions in
the ropes (in N) for each case. Note that 0₁ = 35.0°, 0₂ = 55.0°, 03 = 60.0°, m₁ = 3.00 kg, and m2 = 7.00 kg. (Due to the
nature of this problem, do not use rounded intermediate values-including answers submitted in WebAssign-in your calculations.)
(a)
Τι
WY NY MY
T3
e₁
T₁
=
N
=
N
=
N
(b)
18
Τι
=
Τι
T3
=
|| || ||
=
T
T
Ts
m₂
N
N
N
02
T₂
T3
m₁
You are working with a movie director and investigating a scene with a cowboy sliding off a tree limb and falling onto the saddle of
a moving horse. The distance of the fall is several meters, and the calculation shows a high probability of injury to the cowboy
from the stunt. Let's look at a simpler situation. Suppose the director asks you to have the cowboy step off a platform 2.55 m off
the ground and land on his feet on the ground. The cowboy keeps his legs straight as he falls, but then bends at the knees as
soon as he touches the ground. This allows the center of mass of his body to move through a distance of 0.660 m before his body
comes to rest. (Center of mass will be formally defined in Linear Momentum and Collisions.) You assume this motion to be under
constant acceleration of the center of mass of his body. To assess the degree of danger to the cowboy in this stunt, you wish to
calculate the average force upward on his body from the ground, as a multiple of the cowboy's…
Chapter 28 Solutions
University Physics with Modern Physics (14th Edition)
Ch. 28.1 - (a) If two protons are traveling parallel to each...Ch. 28.2 - An infinitesimal current element located at the...Ch. 28.3 - The accompanying figure shows a circuit that lies...Ch. 28.4 - A solenoid is a wire wound into a helical coil....Ch. 28.5 - Prob. 28.5TYUCh. 28.6 - The accompanying figure shows magnetic field lines...Ch. 28.7 - Prob. 28.7TYUCh. 28.8 - Which of the following materials are attracted to...Ch. 28 - A topic of current interest in physics research is...Ch. 28 - Streams of charged particles emitted from the sun...
Ch. 28 - The text discussed the magnetic field of an...Ch. 28 - Prob. 28.4DQCh. 28 - Pairs of conductors carrying current into or out...Ch. 28 - Suppose you have three long, parallel wires...Ch. 28 - In deriving the force on one of the long,...Ch. 28 - Two concentric, coplanar, circular loops of wire...Ch. 28 - A current was sent through a helical coil spring....Ch. 28 - Prob. 28.10DQCh. 28 - Prob. 28.11DQCh. 28 - Two very long, parallel wires carry equal currents...Ch. 28 - In the circuit shown in Fig. Q28.13, when switch S...Ch. 28 - A metal ring carries a current that causes a...Ch. 28 - Prob. 28.15DQCh. 28 - Prob. 28.16DQCh. 28 - If a magnet is suspended over a container of...Ch. 28 - Prob. 28.18DQCh. 28 - Prob. 28.19DQCh. 28 - A cylinder of iron is placed so that it is free to...Ch. 28 - Prob. 28.1ECh. 28 - Prob. 28.2ECh. 28 - An electron moves at 0.100c as shown in Fig....Ch. 28 - An alpha particle (charge +2e) and an electron...Ch. 28 - A 4.80-C charge is moving at a constant speed of...Ch. 28 - Positive point charges q = +8.00 C and q' = +3.00...Ch. 28 - A negative charge q = 3.60 106 C is located at...Ch. 28 - An electron and a proton are each moving at 735...Ch. 28 - A straight wire carries a 10.0-A current (Fig....Ch. 28 - A short current element dl = (0.500 mm) carries a...Ch. 28 - A long, straight wire lies along the z-axis and...Ch. 28 - Two parallel wires are 5.00 cm apart and carry...Ch. 28 - Prob. 28.13ECh. 28 - A square wire loop 10.0 cm on each side carries a...Ch. 28 - The Magnetic Field from a Lightning Bolt....Ch. 28 - A very long, straight horizontal wire carries a...Ch. 28 - Prob. 28.17ECh. 28 - BIO Bacteria Navigation. Certain bacteria (such as...Ch. 28 - (a) How large a current would a very long,...Ch. 28 - Two long, straight wires, one above the other, are...Ch. 28 - A long, straight wire lies along the y-axis and...Ch. 28 - BIO Transmission Lines and Health. Currents in dc...Ch. 28 - Two long, straight, parallel wires, 10.0 cm apart,...Ch. 28 - A rectangular loop with dimensions 4.20 cm by 9.50...Ch. 28 - Four, long, parallel power lines each carry 100-A...Ch. 28 - Four very long, current-carrying wires in the same...Ch. 28 - Two very long insulated wires perpendicular to...Ch. 28 - Three very long parallel wires each carry current...Ch. 28 - Two long, parallel wires arc separated by a...Ch. 28 - Prob. 28.30ECh. 28 - Lamp Cord Wires. The wires in a household lamp...Ch. 28 - Prob. 28.32ECh. 28 - BIO Currents in the Brain. The magnetic field...Ch. 28 - Calculate the magnitude and direction of the...Ch. 28 - Calculate the magnitude of the magnetic field at...Ch. 28 - A closely wound, circular coil with radius 2.40 cm...Ch. 28 - A single circular current loop 10.0 cm in diameter...Ch. 28 - A closely wound coil has a radius of 6.00 cm and...Ch. 28 - Two concentric circular loops of wire lie on a...Ch. 28 - Figure E28.40 shows, in cross section, several...Ch. 28 - A closed curve encircles several conductors. The...Ch. 28 - As a new electrical technician, you are designing...Ch. 28 - Prob. 28.43ECh. 28 - Prob. 28.44ECh. 28 - A solenoid that is 35 cm long and contains 450...Ch. 28 - A 15.0-cm-long solenoid with radius 0.750 cm is...Ch. 28 - A solenoid is designed to produce a magnetic field...Ch. 28 - A toroidal solenoid has an inner radius of 12.0 cm...Ch. 28 - A magnetic field of 37.2 T has been achieved at...Ch. 28 - An ideal toroidal solenoid (see Example 28.10) has...Ch. 28 - A wooden ring whose mean diameter is 14.0 cm is...Ch. 28 - A toroidal solenoid with 400 turns of wire and a...Ch. 28 - A long solenoid with 60 turns of wire per...Ch. 28 - The current in the windings of a toroidal solenoid...Ch. 28 - A pair of point charges, q = +8.00 C and q' = 5.00...Ch. 28 - At a particular instant, charge q1 = +4.80 106C...Ch. 28 - Two long, parallel transmission lines, 40.0 cm...Ch. 28 - A long, straight wire carries a current of 8.60 A....Ch. 28 - Prob. 28.59PCh. 28 - Prob. 28.60PCh. 28 - An electric bus operates by drawing direct current...Ch. 28 - Figure P28.62 shows an end view of two long,...Ch. 28 - Prob. 28.63PCh. 28 - The long, straight wire AB shown in Fig. P28.64...Ch. 28 - CP Two long, parallel wires hang by 4.00-cm-long...Ch. 28 - The wire semicircles shown in Fig. P28.66 have...Ch. 28 - CALC Helmholtz Coils. Figure P28.67 is a sectional...Ch. 28 - Prob. 28.68PCh. 28 - CALC A long, straight wire with a circular cross...Ch. 28 - CALC The wire shown in Fig. P28.70 is infinitely...Ch. 28 - Prob. 28.71PCh. 28 - Prob. 28.72PCh. 28 - An Infinite Current Sheet. Long, straight...Ch. 28 - Long, straight conductors with square cross...Ch. 28 - A long, straight, solid cylinder, oriented with...Ch. 28 - Prob. 28.76PCh. 28 - DATA You use a teslameter (a Hall-effect device)...Ch. 28 - DATA A pair of long, rigid metal rods, each of...Ch. 28 - CP Two long, straight conducting wires with linear...Ch. 28 - Prob. 28.80CPCh. 28 - BIO STUDYING MAGNETIC BACTERIA. Some types of...Ch. 28 - Prob. 28.82PPCh. 28 - The solenoid is removed from the enclosure and...
Additional Science Textbook Solutions
Find more solutions based on key concepts
15.1 What purpose do the bla and lacZ genes serve in the plasmid vector ?
Genetic Analysis: An Integrated Approach (3rd Edition)
48. Four solutions of unknown NaOH concentration are titrated with solutions of HCl. The following table lists ...
Introductory Chemistry (6th Edition)
1. ___ Mitosis 2. ___ Meiosis 3. __ Homologous chromosomes 4. __ Crossing over 5. __ Cytokinesis A. Cytoplasmic...
Microbiology with Diseases by Body System (5th Edition)
Fibrous connective tissue consists of ground substance and fibers that provide strength, support, and flexibili...
Human Biology: Concepts and Current Issues (8th Edition)
16. Explain some of the reasons why the human species has been able to expand in number and distribution to a g...
Campbell Biology: Concepts & Connections (9th Edition)
Police Captain Jeffers has suffered a myocardial infarction. a. Explain to his (nonmedically oriented) family w...
Human Physiology: An Integrated Approach (8th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A box of mass m = 2.00 kg is released from rest at the top of an inclined plane as seen in the figure. The box starts out at height h =0.200 m above the top of the table, the table height is H = 2.00 m, and 0 = 41.0°. H m (a) What is the acceleration (in m/s²) of the box while it slides down the incline? m/s² (b) What is the speed (in m/s) of the box when it leaves the incline? m/s (c) At what horizontal distance (in m) from the end of the table will the box hit the ground? m (d) How long (in s) from when the box is released does it hit the ground? S (e) Does the box's mass affect any of your above answers? Yes Noarrow_forward(a) A sphere made of rubber has a density of 0.940 g/cm³ and a radius of 7.00 cm. It falls through air of density 1.20 kg/m³ and has a drag coefficient of 0.500. What is its terminal speed (in m/s)? m/s (b) From what height (in m) would the sphere have to be dropped to reach this speed if it fell without air resistance? marrow_forwardThe systems shown below are in equilibrium. If the spring scales are calibrated in newtons, what do they read? Ignore the masses of the pulleys and strings and assume the pulleys and the incline are frictionless. (Let m = 2.19 kg and € = 29.0°.) scale in (a) N N scale in (b) scale in (c) N scale in (d) N a C m m m m m b d m Ꮎarrow_forward
- An elevator car has two equal masses attached to the ceiling as shown. (Assume m = 3.10 kg.) m m T₁ T2 (a) The elevator ascends with an acceleration of magnitude 2.00 m/s². What are the tensions in the two strings? (Enter your answers in N.) = N T₁ Τι = N (b) The maximum tension the strings can withstand is 78.8 N. What is the maximum acceleration of the elevator so that a string does not break? (Enter the magnitude in m/s².) m/s²arrow_forward(a) At what speed (in m/s) will a proton move in a circular path of the same radius as an electron that travels at 7.85 x 100 m/s perpendicular to the Earth's magnetic field at an altitude where the field strength is 1.20 x 10-5 T? 4.27e3 m/s (b) What would the radius (in m) of the path be if the proton had the same speed as the electron? 7.85e6 x m (c) What would the radius (in m) be if the proton had the same kinetic energy as the electron? 195.38 x m (d) What would the radius (in m) be if the proton had the same momentum as the electron? 3.7205 marrow_forward! Required information The block shown is made of a magnesium alloy, for which E = 45 GPa and v = 0.35. Know that σx = -185 MPa. NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. 25 mm B D 40 mm 100 mm Determine the magnitude of Oy for which the change in the height of the block will be zero. The magnitude of Oy is MPa.arrow_forward
- The rigid bar ABC is supported by two links, AD and BE, of uniform 37.5 × 6-mm rectangular cross section and made of a mild steel that is assumed to be elastoplastic with E = 200 GPa and σy= 250 MPa. The magnitude of the force Q applied at B is gradually increased from zero to 265 kN and a = 0.640 m. 1.7 m 1 m D A B 2.64 m E Determine the value of the normal stress in each link. The value of the normal stress in link AD is The value of the normal stress in link BE is 250 MPa. MPa.arrow_forwardTwo tempered-steel bars, each 16 in. thick, are bonded to a ½ -in. mild-steel bar. This composite bar is subjected as shown to a centric axial load of magnitude P. Both steels are elastoplastic with E= 29 × 106 psi and with yield strengths equal to 100 ksi and 50 ksi, respectively, for the tempered and mild steel. The load P is gradually increased from zero until the deformation of the bar reaches a maximum value dm = 0.04 in. and then decreased back to zero. Take L = 15 in. NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. 2.0 in. in. 3 in. 3 16 in. Determine the maximum stress in the tempered-steel bars. The maximum stress in the tempered-steel bars is ksi.arrow_forwardAmmonia enters the compressor of an industrial refrigeration plant at 2 bar, -10°C with a mass flow rate of 15 kg/min and is compressed to 12 bar, 140°C. Heat transfer from the compressor to its surroundings occurs at a rate of 6 kW. For steady-state operation, calculate, (a) the power input to the compressor, in kW, Answer (b) the entropy production rate, in kW/K, for a control volume encompassing the compressor and its immediate surroundings such that heat transfer occurs at 300 K.arrow_forward
- No chatgpt pls will upvotearrow_forwardShown to the right is a block of mass m=5.71kgm=5.71kg on a ramp that makes an angle θ=24.1∘θ=24.1∘ with the horizontal. This block is being pushed by a horizontal force, F=229NF=229N. The coefficient of kinetic friction between the two surfaces is μ=0.51μ=0.51. Enter an expression for the acceleration of the block up the ramp using variables from the problem statement together with gg for the acceleration due to gravity. a=arrow_forwardIf the density and atomic mass of copper are respectively 8.80 x 103 kg/m³ and 63.5 kg/kmol (note that 1 kmol = 1,000 mol), and copper has one free electron per copper atom, determine the following. (a) the drift speed of the electrons in a 10 gauge copper wire (2.588 mm in diameter) carrying a 13.5 A current 1.988-4 See if you can obtain an expression for the drift speed of electrons in a copper wire in terms of the current in the wire, the diameter of the wire, the molecular weight and mass density of copper, Avogadro's number, and the charge on an electron. m/s (b) the Hall voltage if a 2.68 T field is applied perpendicular to the wire 3.34e-6 x Can you start with basic equations for the electric and magnetic forces acting on the electrons moving through the wire and obtain a relationship between the magnitude of the electric and magnetic field and the drift speed of the electrons? How is the magnitude of the electric field related to the Hall voltage and the diameter of the wire? Varrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
What is Electromagnetic Induction? | Faraday's Laws and Lenz Law | iKen | iKen Edu | iKen App; Author: Iken Edu;https://www.youtube.com/watch?v=3HyORmBip-w;License: Standard YouTube License, CC-BY