Chapter 28, Problem 28.21E

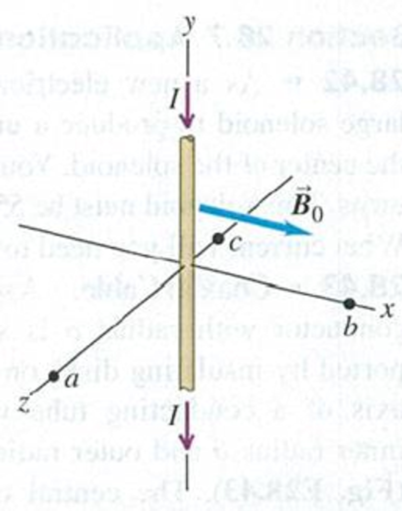
A long, straight wire lies along the y-axis and carries a current I = 8.00 A in the −y-direction (Fig. E28.21). In addition to the magnetic field due to the current in the wire, a uniform magnetic field $\stackrel{\to }{{\text{B}}_0}$ with magnitude 1.50 × 10⁻⁶T is in the +x-direction. What is the total field (magnitude and direction) at the following points in the xz-plane: (a) x = 0, z = 1.00 m; (b) x = 1.00 m, z = 0; (c) x = 0, z = −0.25 m?

Figure E28.21