
(a)
A spreadsheet for
(a)
Answer to Problem 46AP
A spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.015932 | 25.1067 |
| 0.405 | 0.019602 | 20.66116 |
| 0.41 | 0.024117 | 17.00046 |
| 0.415 | 0.029673 | 13.98578 |
| 0.42 | 0.036508 | 11.50433 |
| 0.425 | 0.044918 | 9.461686 |
| 0.43 | 0.055264 | 7.780834 |
| 0.435 | 0.067995 | 6.397529 |
| 0.44 | 0.083657 | 5.259572 |
| 0.445 | 0.102927 | 4.323453 |
| 0.45 | 0.126637 | 3.553464 |
| 0.455 | 0.155807 | 2.92028 |
| 0.46 | 0.191697 | 2.39962 |
| 0.465 | 0.235855 | 1.97155 |
| 0.47 | 0.290184 | 1.619662 |
| 0.475 | 0.357027 | 1.330432 |
| 0.48 | 0.439268 | 1.092727 |
| 0.485 | 0.540454 | 0.897394 |
| 0.495 | 0.818117 | 0.605048 |
| 0.5 | 1.006569 | 0.496737 |
| 0.505 | 1.238432 | 0.407774 |
| 0.51 | 1.523704 | 0.334711 |
| 0.515 | 1.874688 | 0.274712 |
| 0.52 | 2.306521 | 0.225448 |
| 0.525 | 2.837827 | 0.185001 |
| 0.53 | 3.491518 | 0.151796 |
| 0.535 | 4.295787 | 0.124541 |
| 0.54 | 5.285319 | 0.10217 |
| 0.545 | 6.502788 | 0.08381 |
| 0.55 | 8.000701 | 0.068744 |
| 0.555 | 9.843657 | 0.056381 |
| 0.56 | 12.11114 | 0.046238 |
| 0.565 | 14.90093 | 0.037917 |
| 0.57 | 18.33335 | 0.031091 |
| 0.575 | 22.55642 | 0.025492 |
| 0.58 | 27.75228 | 0.020899 |
| 0.585 | 34.145 | 0.017133 |
| 0.59 | 42.01028 | 0.014044 |
| 0.595 | 51.68732 | 0.011512 |
| 0.6 | 63.59346 | 0.009435 |
A spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.005274 | 75.84672 |
| 0.405 | 0.0064 | 63.28565 |
| 0.41 | 0.007766 | 52.79679 |
| 0.415 | 0.009423 | 44.03979 |
| 0.42 | 0.011435 | 36.72991 |
| 0.425 | 0.013876 | 30.62901 |
| 0.43 | 0.016838 | 25.53795 |
| 0.435 | 0.020432 | 21.29022 |
| 0.44 | 0.024793 | 17.74668 |
| 0.445 | 0.030086 | 14.79101 |
| 0.45 | 0.036508 | 12.32605 |
| 0.455 | 0.044301 | 10.27061 |
| 0.46 | 0.053758 | 8.556892 |
| 0.465 | 0.065233 | 7.128278 |
| 0.47 | 0.079158 | 5.937492 |
| 0.475 | 0.096055 | 4.945067 |
| 0.48 | 0.11656 | 4.118066 |
| 0.485 | 0.141441 | 3.428998 |
| 0.495 | 0.20827 | 2.376718 |
| 0.5 | 0.252728 | 1.978408 |
| 0.505 | 0.306677 | 1.646686 |
| 0.51 | 0.372141 | 1.370449 |
| 0.515 | 0.451579 | 1.140443 |
| 0.52 | 0.547974 | 0.948949 |
| 0.525 | 0.664947 | 0.789537 |
| 0.53 | 0.806888 | 0.656844 |
| 0.535 | 0.979129 | 0.546404 |
| 0.54 | 1.188137 | 0.454493 |
| 0.545 | 1.44176 | 0.37801 |
| 0.55 | 1.749522 | 0.314372 |
| 0.555 | 2.122981 | 0.261425 |
| 0.56 | 2.576159 | 0.217378 |
| 0.565 | 3.126073 | 0.180738 |
| 0.57 | 3.793374 | 0.150262 |
| 0.575 | 4.603119 | 0.124915 |
| 0.58 | 5.585715 | 0.103836 |
| 0.585 | 6.778058 | 0.086308 |
| 0.59 | 8.224923 | 0.071733 |
| 0.595 | 9.98064 | 0.059615 |
| 0.6 | 12.11114 | 0.049541 |
A spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.002004 | 199.5582 |
| 0.405 | 0.002403 | 168.5349 |
| 0.41 | 0.002881 | 142.3127 |
| 0.415 | 0.003454 | 120.1526 |
| 0.42 | 0.004141 | 101.4283 |
| 0.425 | 0.004964 | 85.60991 |
| 0.43 | 0.005952 | 72.24847 |
| 0.435 | 0.007135 | 60.96416 |
| 0.44 | 0.008554 | 51.43551 |
| 0.445 | 0.010256 | 43.39059 |
| 0.45 | 0.012295 | 36.59933 |
| 0.455 | 0.014741 | 30.86719 |
| 0.46 | 0.017672 | 26.02967 |
| 0.465 | 0.021187 | 21.9477 |
| 0.47 | 0.0254 | 18.50372 |
| 0.475 | 0.030452 | 15.59839 |
| 0.48 | 0.036508 | 13.14778 |
| 0.485 | 0.043769 | 11.08098 |
| 0.495 | 0.062909 | 7.868498 |
| 0.5 | 0.07542 | 6.629515 |
| 0.505 | 0.09042 | 5.585066 |
| 0.51 | 0.108402 | 4.704703 |
| 0.515 | 0.129961 | 3.962729 |
| 0.52 | 0.155807 | 3.337456 |
| 0.525 | 0.186794 | 2.810585 |
| 0.53 | 0.223943 | 2.366674 |
| 0.535 | 0.26848 | 1.992698 |
| 0.54 | 0.321875 | 1.67767 |
| 0.545 | 0.385889 | 1.412324 |
| 0.55 | 0.462633 | 1.188846 |
| 0.555 | 0.554641 | 1.000647 |
| 0.56 | 0.664947 | 0.842173 |
| 0.565 | 0.79719 | 0.70874 |
| 0.57 | 0.955733 | 0.596401 |
| 0.575 | 1.145807 | 0.50183 |
| 0.58 | 1.373682 | 0.422223 |
| 0.585 | 1.646877 | 0.355218 |
| 0.59 | 1.974404 | 0.298824 |
| 0.595 | 2.367069 | 0.251366 |
| 0.6 | 2.837827 | 0.211429 |
Explanation of Solution
Given information: Th first symbol i.e. Euler’s number is
It is given that the expression for the current-voltage characteristic curve for a semiconductor diode as a function of temperature
Here,
Formula to calculate the resistance across the diode is,
Here,
The value of magnitude of electron charge is
The value of Boltzmann’s constant is
The value of voltage across the diode varies from
From equation (1), formula to calculate the current across a semiconductor diode temperature
Here,
Substitute
Thus, the current across a semiconductor diode temperature
From equation (2), formula to calculate the resistance across the diode is,
Here,
Substitute
Thus, the resistance across the diode is
As the value of voltage across the diode varies from
Thus, a spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.015932 | 25.1067 |
| 0.405 | 0.019602 | 20.66116 |
| 0.41 | 0.024117 | 17.00046 |
| 0.415 | 0.029673 | 13.98578 |
| 0.42 | 0.036508 | 11.50433 |
| 0.425 | 0.044918 | 9.461686 |
| 0.43 | 0.055264 | 7.780834 |
| 0.435 | 0.067995 | 6.397529 |
| 0.44 | 0.083657 | 5.259572 |
| 0.445 | 0.102927 | 4.323453 |
| 0.45 | 0.126637 | 3.553464 |
| 0.455 | 0.155807 | 2.92028 |
| 0.46 | 0.191697 | 2.39962 |
| 0.465 | 0.235855 | 1.97155 |
| 0.47 | 0.290184 | 1.619662 |
| 0.475 | 0.357027 | 1.330432 |
| 0.48 | 0.439268 | 1.092727 |
| 0.485 | 0.540454 | 0.897394 |
| 0.495 | 0.818117 | 0.605048 |
| 0.5 | 1.006569 | 0.496737 |
| 0.505 | 1.238432 | 0.407774 |
| 0.51 | 1.523704 | 0.334711 |
| 0.515 | 1.874688 | 0.274712 |
| 0.52 | 2.306521 | 0.225448 |
| 0.525 | 2.837827 | 0.185001 |
| 0.53 | 3.491518 | 0.151796 |
| 0.535 | 4.295787 | 0.124541 |
| 0.54 | 5.285319 | 0.10217 |
| 0.545 | 6.502788 | 0.08381 |
| 0.55 | 8.000701 | 0.068744 |
| 0.555 | 9.843657 | 0.056381 |
| 0.56 | 12.11114 | 0.046238 |
| 0.565 | 14.90093 | 0.037917 |
| 0.57 | 18.33335 | 0.031091 |
| 0.575 | 22.55642 | 0.025492 |
| 0.58 | 27.75228 | 0.020899 |
| 0.585 | 34.145 | 0.017133 |
| 0.59 | 42.01028 | 0.014044 |
| 0.595 | 51.68732 | 0.011512 |
| 0.6 | 63.59346 | 0.009435 |
From equation (1), formula to calculate the current across a semiconductor diode temperature
Here,
Substitute
Thus, the current across a semiconductor diode temperature
From equation (2), formula to calculate the resistance across the diode is,
Here,
Substitute
Thus, the resistance across the diode is
As the value of voltage across the diode varies from
Thus, a spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.005274 | 75.84672 |
| 0.405 | 0.0064 | 63.28565 |
| 0.41 | 0.007766 | 52.79679 |
| 0.415 | 0.009423 | 44.03979 |
| 0.42 | 0.011435 | 36.72991 |
| 0.425 | 0.013876 | 30.62901 |
| 0.43 | 0.016838 | 25.53795 |
| 0.435 | 0.020432 | 21.29022 |
| 0.44 | 0.024793 | 17.74668 |
| 0.445 | 0.030086 | 14.79101 |
| 0.45 | 0.036508 | 12.32605 |
| 0.455 | 0.044301 | 10.27061 |
| 0.46 | 0.053758 | 8.556892 |
| 0.465 | 0.065233 | 7.128278 |
| 0.47 | 0.079158 | 5.937492 |
| 0.475 | 0.096055 | 4.945067 |
| 0.48 | 0.11656 | 4.118066 |
| 0.485 | 0.141441 | 3.428998 |
| 0.495 | 0.20827 | 2.376718 |
| 0.5 | 0.252728 | 1.978408 |
| 0.505 | 0.306677 | 1.646686 |
| 0.51 | 0.372141 | 1.370449 |
| 0.515 | 0.451579 | 1.140443 |
| 0.52 | 0.547974 | 0.948949 |
| 0.525 | 0.664947 | 0.789537 |
| 0.53 | 0.806888 | 0.656844 |
| 0.535 | 0.979129 | 0.546404 |
| 0.54 | 1.188137 | 0.454493 |
| 0.545 | 1.44176 | 0.37801 |
| 0.55 | 1.749522 | 0.314372 |
| 0.555 | 2.122981 | 0.261425 |
| 0.56 | 2.576159 | 0.217378 |
| 0.565 | 3.126073 | 0.180738 |
| 0.57 | 3.793374 | 0.150262 |
| 0.575 | 4.603119 | 0.124915 |
| 0.58 | 5.585715 | 0.103836 |
| 0.585 | 6.778058 | 0.086308 |
| 0.59 | 8.224923 | 0.071733 |
| 0.595 | 9.98064 | 0.059615 |
| 0.6 | 12.11114 | 0.049541 |
From equation (1), formula to calculate the current across a semiconductor diode temperature
Here,
Substitute
Thus, the current across a semiconductor diode temperature
From equation (2), formula to calculate the resistance across the diode is,
Here,
Substitute
Thus, the resistance across the diode is
As the value of voltage across the diode varies from
Thus, a spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.002004 | 199.5582 |
| 0.405 | 0.002403 | 168.5349 |
| 0.41 | 0.002881 | 142.3127 |
| 0.415 | 0.003454 | 120.1526 |
| 0.42 | 0.004141 | 101.4283 |
| 0.425 | 0.004964 | 85.60991 |
| 0.43 | 0.005952 | 72.24847 |
| 0.435 | 0.007135 | 60.96416 |
| 0.44 | 0.008554 | 51.43551 |
| 0.445 | 0.010256 | 43.39059 |
| 0.45 | 0.012295 | 36.59933 |
| 0.455 | 0.014741 | 30.86719 |
| 0.46 | 0.017672 | 26.02967 |
| 0.465 | 0.021187 | 21.9477 |
| 0.47 | 0.0254 | 18.50372 |
| 0.475 | 0.030452 | 15.59839 |
| 0.48 | 0.036508 | 13.14778 |
| 0.485 | 0.043769 | 11.08098 |
| 0.495 | 0.062909 | 7.868498 |
| 0.5 | 0.07542 | 6.629515 |
| 0.505 | 0.09042 | 5.585066 |
| 0.51 | 0.108402 | 4.704703 |
| 0.515 | 0.129961 | 3.962729 |
| 0.52 | 0.155807 | 3.337456 |
| 0.525 | 0.186794 | 2.810585 |
| 0.53 | 0.223943 | 2.366674 |
| 0.535 | 0.26848 | 1.992698 |
| 0.54 | 0.321875 | 1.67767 |
| 0.545 | 0.385889 | 1.412324 |
| 0.55 | 0.462633 | 1.188846 |
| 0.555 | 0.554641 | 1.000647 |
| 0.56 | 0.664947 | 0.842173 |
| 0.565 | 0.79719 | 0.70874 |
| 0.57 | 0.955733 | 0.596401 |
| 0.575 | 1.145807 | 0.50183 |
| 0.58 | 1.373682 | 0.422223 |
| 0.585 | 1.646877 | 0.355218 |
| 0.59 | 1.974404 | 0.298824 |
| 0.595 | 2.367069 | 0.251366 |
| 0.6 | 2.837827 | 0.211429 |
Conclusion:
Therefore, a spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.015932 | 25.1067 |
| 0.405 | 0.019602 | 20.66116 |
| 0.41 | 0.024117 | 17.00046 |
| 0.415 | 0.029673 | 13.98578 |
| 0.42 | 0.036508 | 11.50433 |
| 0.425 | 0.044918 | 9.461686 |
| 0.43 | 0.055264 | 7.780834 |
| 0.435 | 0.067995 | 6.397529 |
| 0.44 | 0.083657 | 5.259572 |
| 0.445 | 0.102927 | 4.323453 |
| 0.45 | 0.126637 | 3.553464 |
| 0.455 | 0.155807 | 2.92028 |
| 0.46 | 0.191697 | 2.39962 |
| 0.465 | 0.235855 | 1.97155 |
| 0.47 | 0.290184 | 1.619662 |
| 0.475 | 0.357027 | 1.330432 |
| 0.48 | 0.439268 | 1.092727 |
| 0.485 | 0.540454 | 0.897394 |
| 0.495 | 0.818117 | 0.605048 |
| 0.5 | 1.006569 | 0.496737 |
| 0.505 | 1.238432 | 0.407774 |
| 0.51 | 1.523704 | 0.334711 |
| 0.515 | 1.874688 | 0.274712 |
| 0.52 | 2.306521 | 0.225448 |
| 0.525 | 2.837827 | 0.185001 |
| 0.53 | 3.491518 | 0.151796 |
| 0.535 | 4.295787 | 0.124541 |
| 0.54 | 5.285319 | 0.10217 |
| 0.545 | 6.502788 | 0.08381 |
| 0.55 | 8.000701 | 0.068744 |
| 0.555 | 9.843657 | 0.056381 |
| 0.56 | 12.11114 | 0.046238 |
| 0.565 | 14.90093 | 0.037917 |
| 0.57 | 18.33335 | 0.031091 |
| 0.575 | 22.55642 | 0.025492 |
| 0.58 | 27.75228 | 0.020899 |
| 0.585 | 34.145 | 0.017133 |
| 0.59 | 42.01028 | 0.014044 |
| 0.595 | 51.68732 | 0.011512 |
| 0.6 | 63.59346 | 0.009435 |
A spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.005274 | 75.84672 |
| 0.405 | 0.0064 | 63.28565 |
| 0.41 | 0.007766 | 52.79679 |
| 0.415 | 0.009423 | 44.03979 |
| 0.42 | 0.011435 | 36.72991 |
| 0.425 | 0.013876 | 30.62901 |
| 0.43 | 0.016838 | 25.53795 |
| 0.435 | 0.020432 | 21.29022 |
| 0.44 | 0.024793 | 17.74668 |
| 0.445 | 0.030086 | 14.79101 |
| 0.45 | 0.036508 | 12.32605 |
| 0.455 | 0.044301 | 10.27061 |
| 0.46 | 0.053758 | 8.556892 |
| 0.465 | 0.065233 | 7.128278 |
| 0.47 | 0.079158 | 5.937492 |
| 0.475 | 0.096055 | 4.945067 |
| 0.48 | 0.11656 | 4.118066 |
| 0.485 | 0.141441 | 3.428998 |
| 0.495 | 0.20827 | 2.376718 |
| 0.5 | 0.252728 | 1.978408 |
| 0.505 | 0.306677 | 1.646686 |
| 0.51 | 0.372141 | 1.370449 |
| 0.515 | 0.451579 | 1.140443 |
| 0.52 | 0.547974 | 0.948949 |
| 0.525 | 0.664947 | 0.789537 |
| 0.53 | 0.806888 | 0.656844 |
| 0.535 | 0.979129 | 0.546404 |
| 0.54 | 1.188137 | 0.454493 |
| 0.545 | 1.44176 | 0.37801 |
| 0.55 | 1.749522 | 0.314372 |
| 0.555 | 2.122981 | 0.261425 |
| 0.56 | 2.576159 | 0.217378 |
| 0.565 | 3.126073 | 0.180738 |
| 0.57 | 3.793374 | 0.150262 |
| 0.575 | 4.603119 | 0.124915 |
| 0.58 | 5.585715 | 0.103836 |
| 0.585 | 6.778058 | 0.086308 |
| 0.59 | 8.224923 | 0.071733 |
| 0.595 | 9.98064 | 0.059615 |
| 0.6 | 12.11114 | 0.049541 |
A spreadsheet for
|
(Volts) |
(Amperes) |
|
| 0.4 | 0.002004 | 199.5582 |
| 0.405 | 0.002403 | 168.5349 |
| 0.41 | 0.002881 | 142.3127 |
| 0.415 | 0.003454 | 120.1526 |
| 0.42 | 0.004141 | 101.4283 |
| 0.425 | 0.004964 | 85.60991 |
| 0.43 | 0.005952 | 72.24847 |
| 0.435 | 0.007135 | 60.96416 |
| 0.44 | 0.008554 | 51.43551 |
| 0.445 | 0.010256 | 43.39059 |
| 0.45 | 0.012295 | 36.59933 |
| 0.455 | 0.014741 | 30.86719 |
| 0.46 | 0.017672 | 26.02967 |
| 0.465 | 0.021187 | 21.9477 |
| 0.47 | 0.0254 | 18.50372 |
| 0.475 | 0.030452 | 15.59839 |
| 0.48 | 0.036508 | 13.14778 |
| 0.485 | 0.043769 | 11.08098 |
| 0.495 | 0.062909 | 7.868498 |
| 0.5 | 0.07542 | 6.629515 |
| 0.505 | 0.09042 | 5.585066 |
| 0.51 | 0.108402 | 4.704703 |
| 0.515 | 0.129961 | 3.962729 |
| 0.52 | 0.155807 | 3.337456 |
| 0.525 | 0.186794 | 2.810585 |
| 0.53 | 0.223943 | 2.366674 |
| 0.535 | 0.26848 | 1.992698 |
| 0.54 | 0.321875 | 1.67767 |
| 0.545 | 0.385889 | 1.412324 |
| 0.55 | 0.462633 | 1.188846 |
| 0.555 | 0.554641 | 1.000647 |
| 0.56 | 0.664947 | 0.842173 |
| 0.565 | 0.79719 | 0.70874 |
| 0.57 | 0.955733 | 0.596401 |
| 0.575 | 1.145807 | 0.50183 |
| 0.58 | 1.373682 | 0.422223 |
| 0.585 | 1.646877 | 0.355218 |
| 0.59 | 1.974404 | 0.298824 |
| 0.595 | 2.367069 | 0.251366 |
| 0.6 | 2.837827 | 0.211429 |
(b)
To draw: The graph for
(b)
Answer to Problem 46AP
The graph for
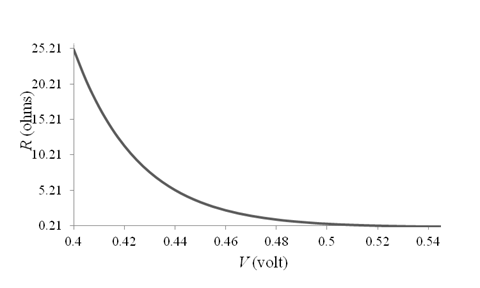
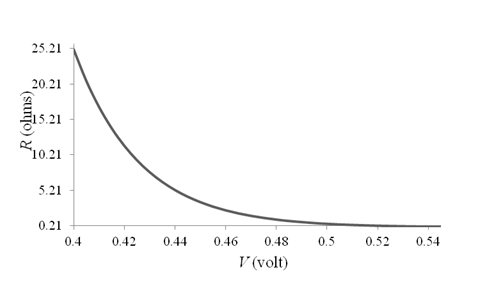
The graph for
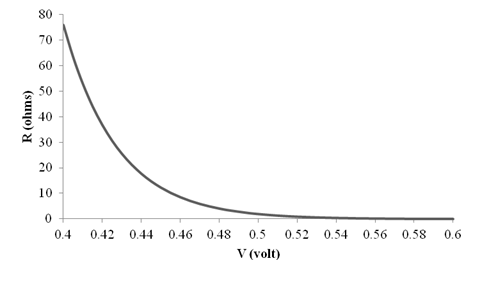
The graph for
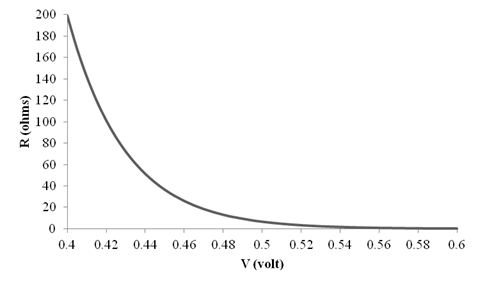
Explanation of Solution
Given information: The first symbol i.e. Euler’s number is
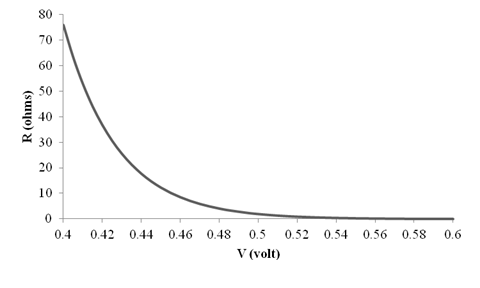
The different values of the
Thus, the graph for
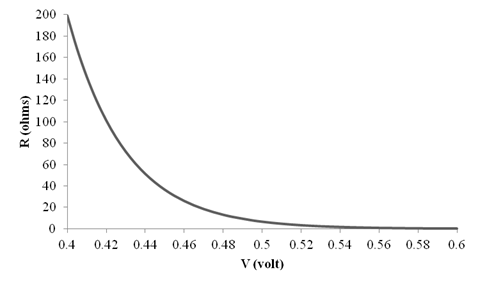
The different values of the
Thus, the graph for
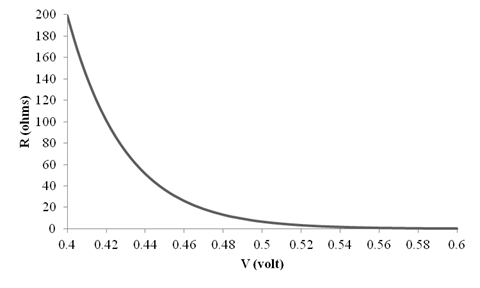
The different values of the
The graph for
Conclusion:
Therefore, the graph for

Therefore, the graph for

Therefore, the graph for
Want to see more full solutions like this?
Chapter 26 Solutions
Physics for Scientists and Engineers with Modern Physics
- Lab 8 Part 3 PHET Wave Interface simulation. I am having trouble with this part of the lab.arrow_forwardMick and Rick are twins born on Earth in the year 2175. Rick grows up to be an Earth-bound robotics technician while Mick becomes an intergalactic astronaut. Mick leaves the Earth on his first space mission in the year 2200 and travels, according to his clock, for 10 years at a speed of 0.75c. Unfortunately, at this point in his journey, the structure of his ship undergoes mechanical breakdown and the ship explodes. How old is Rick when his brother dies?arrow_forwardHi, I have canceled, why did you charge me again?arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax





