Chapter 2.4, Problem 9CE

a.

To determine

To find:two congruent supplementary angles

Answer to Problem 9CE

  $\angle AXB,\angle DXB$

Explanation of Solution

Given information: $\angle AXB=90°$

  

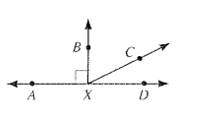
First find $\angle DXB$

As sum of angles on a straight line is equal to $180°$ ,

  $\angle AXB+\angle DXB=180°$

Put $\angle AXB=90°$

  $\begin{array}{l}90°+\angle DXB=180°\\ \Rightarrow \angle DXB=180°-90°=90°\end{array}$

So,

  $\angle DXB=90°$

Now prove that $\angle AXB\cong \angle DXB$

Here, $\angle AXB=\angle DXB=90°$

As angles equal in measures are also congruent,

  $\angle AXB\cong \angle DXB$

Now prove that $\angle AXB,\angle DXB$ are supplementary angles

If sum of two angles is $180°$ then those angles are said to be supplementary.

As $\angle AXB+\angle DXB=180°$ ,

  $\angle AXB,\angle DXB$ are supplementary angles

Therefore,

  $\angle AXB,\angle DXB$ are two congruent supplementary angles.

b.

To determine

To find: two supplementary angles that are not congruent

Answer to Problem 9CE

  $\angle AXC,\angle CXD$

Explanation of Solution

  

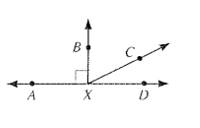
From the figure, it can be observed that $\angle BXD=\angle BXC+\angle CXD$

So,

  $\angle CXD<\angle BXD$

In part a., it has been proved that $\angle BXD=90°$

So,

  $\begin{array}{l}\angle CXD<\angle BXD=90°\\ \Rightarrow \angle CXD<90°=\angle AXB\left\{\because \angle AXB=90°\right\}\\ \Rightarrow \angle CXD<\angle AXB(i)\end{array}$

And

  $\angle AXB<\angle AXC$ (ii)

From (i) and (ii),

  $\angle CXD<\angle AXC$

As two angles which are not equal in measure are not congruent,

  $\angle CXD\cancel{\cong }\angle AXC$

Also,

  $\angle CXD+\angle AXC=180°$ (sum of angles on a straight line is equal to $180°$ )

So,

  $\angle CXD,\angle AXC$ are supplementary angles

(If sum of two angles is $180°$ then such angles are said to be supplementary)

Therefore,

  $\angle CXD,\angle AXC$ are supplementary angles such that $\angle CXD\cancel{\cong }\angle AXC$

So,

  $\angle CXD,\angle AXC$ are two supplementary angles that are not congruent.

c.

To determine

To find:two complementary angles

Answer to Problem 9CE

  $\angle BXC,\angle CXD$ are two complementary angles

Explanation of Solution

  

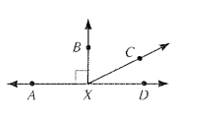
It has already been proved in explanation of part a. that $\angle BXD=90°$

Also,

  $\begin{array}{l}\angle BXD=\angle BXC+\angle CXD\\ \Rightarrow 90°=\angle BXC+\angle CXD\end{array}$

If sum of two angles is $90°$ then such angles are said to be complementary.

Here, $\angle BXC+\angle CXD=90°$

So,

  $\angle BXC,\angle CXD$ are two complementary angles.

d.

To determine

To find: a straight angle

Answer to Problem 9CE

  $\angle AXD$ is a straight angle

Explanation of Solution

  

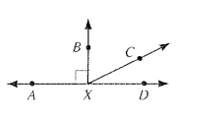
A straight angle is an angle whose sides lie in opposite direction in the same straight line.

In the given figure,

  $\angle AXD$ is an angle such that rays $\overrightarrow{XA},\overrightarrow{XD}$ lie in opposite directions in a same straight line.

So, $\angle AXD$ is a straight angle