
Concept explainers
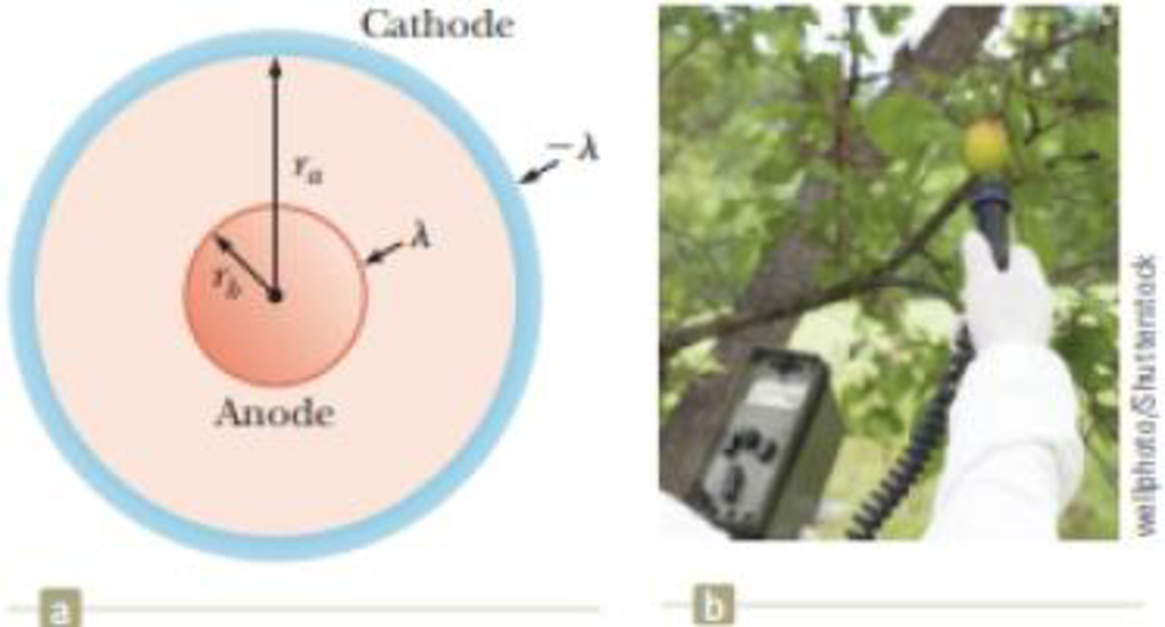
A Geiger–Mueller tube is a
(b) Show that the magnitude of the electric field in the space between cathode and anode is
where r is the distance from the axis of the anode to the point where the field is to be calculated.
Figure P24.42
Want to see the full answer?
Check out a sample textbook solution
Chapter 24 Solutions
Bundle: Physics For Scientists And Engineers With Modern Physics, Loose-leaf Version, 10th + Webassign Printed Access Card For Serway/jewett's Physics For Scientists And Engineers, 10th, Single-term
Additional Science Textbook Solutions
EBK INTRODUCTION TO CHEMISTRY
Organic Chemistry
Fundamentals Of Thermodynamics
Campbell Essential Biology with Physiology (5th Edition)
Brock Biology of Microorganisms (15th Edition)
Loose Leaf For Integrated Principles Of Zoology
- The determined Wile E. Coyote is out once more to try to capture the elusive Road Runner of Loony Tunes fame. The coyote is strapped to a rocket, which provide a constant horizontal acceleration of 15.0 m/s2. The coyote starts off at rest 79.2 m from the edge of a cliff at the instant the roadrunner zips by in the direction of the cliff. If the roadrunner moves with constant speed, find the minimum velocity the roadrunner must have to reach the cliff before the coyote. (proper sig fig in answer)arrow_forwardPROBLEM 4 What is the resultant of the force system acting on the connection shown? 25 F₁ = 80 lbs IK 65° F2 = 60 lbsarrow_forwardThree point-like charges in the attached image are placed at the corners of an equilateral triangle as shown in the figure. Each side of the triangle has a length of 38.0 cm, and the point (C) is located half way between q1 and q3 along the side. Find the magnitude of the electric field at point (C). Let q1 = −2.80 µC, q2 = −3.40 µC, and q3 = −4.50 µC. Thank you.arrow_forward
- STRUCTURES I Homework #1: Force Systems Name: TA: PROBLEM 1 Determine the horizontal and vertical components of the force in the cable shown. PROBLEM 2 The horizontal component of force F is 30 lb. What is the magnitude of force F? 6 10 4 4 F = 600lbs F = ?arrow_forwardThe determined Wile E. Coyote is out once more to try to capture the elusive Road Runner of Loony Tunes fame. The coyote is strapped to a rocket, which provide a constant horizontal acceleration of 15.0 m/s2. The coyote starts off at rest 79.2 m from the edge of a cliff at the instant the roadrunner zips by in the direction of the cliff. If the roadrunner moves with constant speed, find the minimum velocity the roadrunner must have to reach the cliff before the coyote. (proper sig fig)arrow_forwardHello, I need some help with calculations for a lab, it is Kinematics: Finding Acceleration Due to Gravity. Equations: s=s0+v0t+1/2at2 and a=gsinθ. The hypotenuse,r, is 100cm (given) and a height, y, is 3.5 cm (given). How do I find the Angle θ1? And, for distance traveled, s, would all be 100cm? For my first observations I recorded four trials in seconds: 1 - 2.13s, 2 - 2.60s, 3 - 2.08s, & 4 - 1.95s. This would all go in the coloumn for time right? How do I solve for the experimental approximation of the acceleration? Help with trial 1 would be great so I can use that as a model for the other trials. Thanks!arrow_forward
- After the countdown at the beginning of a Mario Kart race, Bowser slams on the gas, taking off from rest. Bowser get up to a full speed of 25.5 m/s due to an acceleration of 10.4 m/s2. A)How much time does it take to reach full speed? B) How far does Bowser travel while accelerating?arrow_forwardThe drawing in the image attached shows an edge-on view of two planar surfaces that intersect and are mutually perpendicular. Side 1 has an area of 1.90 m^2, Side 2 has an area of 3.90 m^2, the electric field in magnitude is around 215 N/C. Please find the electric flux magnitude through side 1 and 2 combined if the angle (theta) made between the electric field with side 2 is 30.0 degrees. I believe side 1 is 60 degrees but could be wrong. Thank you.arrow_forwardAfter the countdown at the beginning of a Mario Kart race, Bowser slams on the gas, taking off from rest. Bowser get up to a full speed of 25.5 m/s due to an acceleration of 10.4 m/s2.arrow_forward
- The drawing in the image attached shows an edge-on view of two planar surfaces that intersect and are mutually perpendicular. Side 1 has an area of 1.90 m^2, Side 2 has an area of 3.90 m^2, the electric field in magnitude is around 215 N/C. Please find the electric flux magnitude through side 1 and 2 combined if the angle (theta) made between the electric field with side 2 is 30.0 degrees. Thank you.arrow_forwardThe drawing in the image attached shows an edge-on view of two planar surfaces that intersect and are mutually perpendicular. Surface (1) has an area of 1.90 m^2, while Surface (2) has an area of 3.90 m^2. The electric field in magnitude of 215 N/C. Please find the magnitude of the electric flux through surface (with both 1 and 2 combined) if the angle (theta) made between the electric field with surface (2) is 30.0 degrees. Thank you.arrow_forwardThe drawing in the image attached shows an edge-on view of two planar surfaces that intersect and are mutually perpendicular. Surface (1) has an area of 1.90 m^2, while Surface (2) has an area of 3.90 m^2. The electric field in magnitude of 215 N/C. Please find the magnitude of the electric flux through surface (with both 1 and 2 combined) if the angle (theta) made between the electric field with surface (2) is 30.0 degrees. Thank you.arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





