Chapter 24, Problem 41A

To determine

Each type of cost for all three jobs.

Answer to Problem 41A

Job 1:

Labor cost percentage is $47\%$.

Material cost percentage is $22\%$.

Overhead cost percentage is $31\%$.

Job 2:

Labor cost percentage is $32\%$.

Material cost percentage is $37\%$.

Overhead cost percentage is $31\%$.

Job 3:

Labor cost percentage is $42\%$.

Material cost percentage is $31\%$.

Overhead cost percentage is $27\%$.

Explanation of Solution

Given information:

Manufacturing cost consists of labor costs, material cost and overhead cost. Total manufacturing cost for job $1,2\text{ and 3}$ is given as below.

  

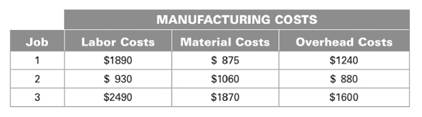
Calculation:

Components of manufacturing cost is given as below.

Job	Labor Cost	Material cost	Overhead cost	Total cost
$1$	$\$1890$	$\$875$	$\$1240$	$\$4005$
$2.$	$\$930$	$\$1060$	$\$880$	$\$2870$
$3.$	$\$2490$	$\$1870$	$\$1600$	$\$5960$

Now we need to find the individual cost percentage for each job. Total cost will be base and individual costs will be percentage.

As we know the proportion to find percentage is given as

  $\frac{P}{B}=\frac{R}{100}$   where, $P=\text{percentage, }B=\text{ base and }R=\text{rate}$

Job 1:

Labor cost $=$$\$1890$ i.e. $P=$$\$1890$ and total manufacturing cost $=$$\$4005$ i.e. $B=$$\$4005$.

Putting these value in standard proportion,

  $\begin{array}{l}\frac{P}{B}=\frac{R}{100}\\ \Rightarrow \frac{1890}{4005}=\frac{R}{100}\text{ {Put }B=4005\text{ and }P=1890\text{}}\\ \text{Applying cross multiplication,}\\ \Rightarrow 4005R=1890\times 100\\ \Rightarrow R=\frac{1890\times 100}{4005}\\ \Rightarrow R=47.191\\ \Rightarrow R=47\text{ {Rounding off to nearest whole number}}\end{array}$

Hence, the labor cost percentage is $47\%$.

Similarly,

Material cost $=$$\$875$ i.e. $P=$$\$875$ and total manufacturing cost $=$$\$4005$ i.e. $B=$$\$4005$.

Putting these value in standard proportion,

  $\begin{array}{l}\frac{P}{B}=\frac{R}{100}\\ \Rightarrow \frac{875}{4005}=\frac{R}{100}\text{ {Put }B=4005\text{ and }P=875\text{}}\\ \text{Applying cross multiplication,}\\ \Rightarrow 4005R=875\times 100\\ \Rightarrow R=\frac{875\times 100}{4005}\\ \Rightarrow R=21.84769\\ \Rightarrow R=22\text{ {Rounding off to nearest whole number}}\end{array}$

Hence, the material cost percentage is $22\%$.

Again,

Overhead cost $=$$\$1240$ i.e. $P=$$\$1240$ and total manufacturing cost $=$$\$4005$ i.e. $B=$$\$4005$

Putting these value in standard proportion,

  $\begin{array}{l}\frac{P}{B}=\frac{R}{100}\\ \Rightarrow \frac{1240}{4005}=\frac{R}{100}\text{ {Put }B=4005\text{ and }P=1240\text{}}\\ \text{Applying cross multiplication,}\\ \Rightarrow 4005R=1240\times 100\\ \Rightarrow R=\frac{1240\times 100}{4005}\\ \Rightarrow R=30.96129\\ \Rightarrow R=31\text{ {Rounding off to nearest whole number}}\end{array}$

Hence, the Overhead cost percentage is $31\%$.

Job 2:

Labor cost $=$$\$930$ i.e. $P=$$\$930$ and total manufacturing cost $=$$\$2870$ i.e. $B=$$\$2870$.

Putting these value in standard proportion,

  $\begin{array}{l}\frac{P}{B}=\frac{R}{100}\\ \Rightarrow \frac{930}{2870}=\frac{R}{100}\text{ {Put }B=2870\text{ and }P=930\text{}}\\ \text{Applying cross multiplication,}\\ \Rightarrow 2870R=930\times 100\\ \Rightarrow R=\frac{930\times 100}{2870}\\ \Rightarrow R=32.4041\\ \Rightarrow R=32\text{ {Rounding off to nearest whole number}}\end{array}$

Hence, the labor cost percentage is $32\%$.

Similarly,

Material cost $=$$\$1060$ i.e. $P=$$\$1060$ and total manufacturing cost $=$$\$2870$ i.e. $B=$$\$2870$.

Putting these value in standard proportion,

  $\begin{array}{l}\frac{P}{B}=\frac{R}{100}\\ \Rightarrow \frac{1060}{2870}=\frac{R}{100}\text{ {Put }B=2870\text{ and }P=1060\text{}}\\ \text{Applying cross multiplication,}\\ \Rightarrow 2870R=1060\times 100\\ \Rightarrow R=\frac{1060\times 100}{2870}\\ \Rightarrow R=36.93379\\ \Rightarrow R=37\text{ {Rounding off to nearest whole number}}\end{array}$

Hence, the material cost percentage is $37\%$.

Again,

Overhead cost $=$$\$880$ i.e. $P=$$\$880$ and total manufacturing cost $=$$\$2870$ i.e. $B=$$\$2870$

Putting these value in standard proportion,

  $\begin{array}{l}\frac{P}{B}=\frac{R}{100}\\ \Rightarrow \frac{880}{2870}=\frac{R}{100}\text{ {Put }B=2870\text{ and }P=880\text{}}\\ \text{Applying cross multiplication,}\\ \Rightarrow 2870R=880\times 100\\ \Rightarrow R=\frac{880\times 100}{2870}\\ \Rightarrow R=30.6620\\ \Rightarrow R=31\text{ {Rounding off to nearest whole number}}\end{array}$

Hence, the Overhead cost percentage is $31\%$.

Job 3:

Labor cost $=$$\$2490$ i.e. $P=$$\$2490$ and total manufacturing cost $=$$\$5960$ i.e. $B=$$\$5960$.

Putting these value in standard proportion,

  $\begin{array}{l}\frac{P}{B}=\frac{R}{100}\\ \Rightarrow \frac{2490}{5960}=\frac{R}{100}\text{ {Put }B=5960\text{ and }P=2490\text{}}\\ \text{Applying cross multiplication,}\\ \Rightarrow 5960R=2490\times 100\\ \Rightarrow R=\frac{2490\times 100}{5960}\\ \Rightarrow R=41.7785\\ \Rightarrow R=42\text{ {Rounding off to nearest whole number}}\end{array}$

Hence, the labor cost percentage is $42\%$.

Similarly,

Material cost $=$$\$1870$ i.e. $P=$$\$1870$ and total manufacturing cost $=$$\$5960$ i.e. $B=$$\$5960$.

Putting these value in standard proportion,

  $\begin{array}{l}\frac{P}{B}=\frac{R}{100}\\ \Rightarrow \frac{1870}{5960}=\frac{R}{100}\text{ {Put }B=5960\text{ and }P=1870\text{}}\\ \text{Applying cross multiplication,}\\ \Rightarrow 5960R=1870\times 100\\ \Rightarrow R=\frac{1870\times 100}{5960}\\ \Rightarrow R=31.3758\\ \Rightarrow R=31\text{ {Rounding off to nearest whole number}}\end{array}$

Hence, the material cost percentage is $31\%$.

Again, Overhead cost $=$$\$1600$ i.e. $P=$$\$1600$ and total manufacturing cost $=$$\$5960$ i.e. $B=$$\$5960$.

Putting these value in standard proportion,

  $\begin{array}{l}\frac{P}{B}=\frac{R}{100}\\ \Rightarrow \frac{1600}{5960}=\frac{R}{100}\text{ {Put }B=5960\text{ and }P=1600\text{}}\\ \text{Applying cross multiplication,}\\ \Rightarrow 5960R=1600\times 100\\ \Rightarrow R=\frac{1600\times 100}{5960}\\ \Rightarrow R=26.845637\\ \Rightarrow R=27\text{ {Rounding off to nearest whole number}}\end{array}$

Hence, the overhead cost percentage is $27\%$.

Thus,

Job 1:

Labor cost percentage is $47\%$.

Material cost percentage is $22\%$.

Overhead cost percentage is $31\%$.

Job 2:

Labor cost percentage is $32\%$.

Material cost percentage is $37\%$.

Overhead cost percentage is $31\%$.

Job 3:

Labor cost percentage is $42\%$.

Material cost percentage is $31\%$.

Overhead cost percentage is $27\%$.