
a.
To Describe: The motion of the particle for
a.
Answer to Problem 37E
In the beginning, the particle was moving in a positive direction until
Explanation of Solution
Given:
The position
And
Using the power rule, the derivative of
This derivative will represent velocity:
Find the velocity when it equal to
As the particle will have zero velocity at maximum or minimum, this will tell us the time when the particle reached its maximum/minimum.
Use the quadratic formula:
Therefore, until approximately
Once the particle's velocity was
From that point on, the particle again changed direction and moved in a positive direction.
b.
To Describe: The time, in which the particle speeds up and slows down.
b.
Answer to Problem 37E
At the intervals
At the intervals
Explanation of Solution
Given:
The position
Given the equation:
When velocity and acceleration have the same sign (both positive or both negative), a particle is speeding up, while a particle is slowing down when the signs are opposite (one is positive and the other is negative).
From part a) The velocity is positive when
Find the second derivative of
Set the above equation equal to
Test the value between 0 and
So, Take
Test the value greater than
So, take
Hence, the acceleration is positive when
At the interval,
At the interval,
At the interval,
Both acceleration and velocity are positive for
So,
At the intervals
At the intervals
c.
To Find: The time the particle changing its direction.
c.
Answer to Problem 37E
The particle changing its direction at
Explanation of Solution
Given:
The position
The equation:
When the particle velocity is
As mentioned in part
d.
To Find: The time at which the particle is at rest.
d.
Answer to Problem 37E
At
Explanation of Solution
Given:
The position
The equation:
When the particle velocity is
From part
So, at
e.
To Describe: The velocity and the speed of the particle.
e.
Answer to Problem 37E
Velocity:
Initially, the velocity was positive, but it stopped increasing, and then it became negative, and then it increased again, and then it became positive again then continue to increase.
Speed:
During the first part of the equation, the speed drops to zero at
Explanation of Solution
Given:
The position
The equation:
State the velocity and the speed of the particle:
It's calculates from part
Hence at the time at
There is a positive velocity at first since,
At
Thereafter, it will increase to infinity again.
Due to the initial decrease in velocity, the speed will also decrease until
It then increases until
Diagrammatic representation is as follows:
The graph of
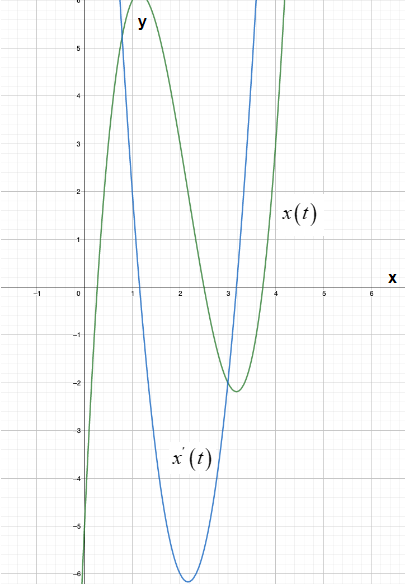
e.
To Describe: The time in which the particle at the point
e.
Answer to Problem 37E
The time in which the particle at the point
Explanation of Solution
Given:
The position
Given the equation:
Find the time, the particle is at
Position of the particle at time
So, set
Subtract
Find the value of
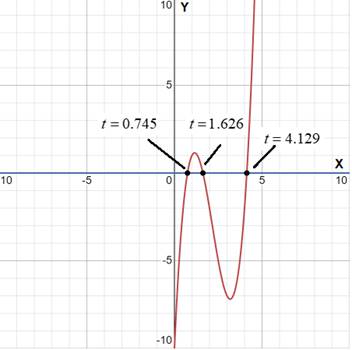
Thus, the values of
Chapter 2 Solutions
Advanced Placement Calculus Graphical Numerical Algebraic Sixth Edition High School Binding Copyright 2020
- 1. A solution to the differential equation y′′ + 4y′ + 13y = 0 isA. y(t) = e^2t cos 3t B. y(t) = te^2t cos 3t C. y(t) = e^−2t sin 3t D. None of thesearrow_forward2. The appropriate guess for the particular solution to the differential equationy′′ + 3y′ + 2y = 2x + 3e^−x isA. A + Bx + Ce^−x B. A + Bx + Cxe^−x C. Ax + Bx^2 + Ce−^x D. Ax + Bx^2 + Cxe^−xarrow_forward23. Network Analysis The figure shows the flow of traffic (in vehicles per hour) through a network of streets. 200 100- -100 200 (a) Solve this system for i = 1, 2, 3, 4. (b) Find the traffic flow when x = 0. (c) Find the traffic flow when x = 100. (d) Find the traffic flow when x, = 2x₂.arrow_forward
- 2\int_{-3/2}^{3/2} \sqrt{4u^2+2} duarrow_forward2. Consider the following: Prove that x, x2, and 1/x are the solutions to the homogeneous equation corresponding to x³y"" + x²y" + 2xy' + 2y = 2x4. b. use variation of parameters to find a particular solution and complete the general solution to the differential equation. I am interested in process. You may use a computer for integration, finding determinants and doing Kramer's.arrow_forward3. A spring is stretched 6 in. by a mass that weighs 8 lb. The mass is attached to a dashpot mechanism that has a damping constant of 0.25 lb-sec./ft. and is acted on by an external force of 4 cos 2t lb. a. Set-up the differential equation and initial value problem for the system. b. Write the function in phase-amplitude form. C. Determine the transient solution to the system. Show your work. d. Determine the steady state of this system. Show your work. e. Is the system underdamped, overdamped or critically damped? Explain what this means for the system.arrow_forward
- 4. Suppose that you have a circuit with a resistance of 20, inductance of 14 H and a capacitance of 11 F. An EMF with equation of E(t) = 6 cos 4t supplies a continuous charge 60 to the circuit. Suppose that the q(0)= 8 V and the q'(0)=7. Use this information to answer the following questions a. Find the function that models the charge of this circuit. b. Is the circuit underdamped, overdamped or critically damped?arrow_forward1. Solve the initial value problem: y" -11y' + 30y = x³e6x y(0) 11, y'(0) = 36 =arrow_forwardWhat is the particular solution to the differential equation y′′ + y = 1/cos t ?arrow_forward
- Which of the following is the general solution to y′′ + 4y = e^2t + 12 sin(2t) ?A. y(t) = c1 cos(2t) + c2 sin(2t) + 1/8 e^2t − 3t cos(2t)B. y(t) = c1e^2t + c2e^−2t + 1/4 te^2t − 3t cos(2t)C. y(t) = c1 + c2e^−4t + 1/12 te^2t − 3t cos(2t)D. y(t) = c1 cos(2t) + c2 sin(2t) + 1/8 e^2t + 3 sin(2t)E. None of the above. Please include all steps! Thank you!arrow_forwardShow that i cote +1 = cosec 20 tan 20+1 = sec² O २ cos² + sin 20 = 1 using pythagon's theoremarrow_forwardFind the general solution to the differential equationarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





