
a.
To calculate: The instantaneous velocity.
a.
Answer to Problem 22E
The instantaneous velocity is
Explanation of Solution
Given information:
The function is
Concept used:
The formula used is
Calculation:
The function is
Differentiate the function with respect to time
Conclusion: The instantaneous velocity of the particle is.
b.
To calculate: The acceleration of the particle.
b.
Answer to Problem 22E
The acceleration of the particle is
Explanation of Solution
Given information:
The function is
Concept used:
The formula used is
Calculation:
The function is
Differentiate the function with respect to time
Differentiate the function again with respect to time
Conclusion: The acceleration of the particle is
c.
To calculate: The time at which the particle is at rest.
c.
Answer to Problem 22E
The times when particle is at rest are
Explanation of Solution
Given information:
The function is
Concept used:
The particle will be in rest when the velocity of the particle becomes zero,
Calculation:
The function is
Differentiate the function with respect to time
Equate the velocity to zero.
Solve further.
Conclusion: The particle will be in rest when
d.
To calculate: The time when particle changes its direction.
d.
Explanation of Solution
Given information:
The function is
Calculation:
The function is
The graph of the function is shown below.
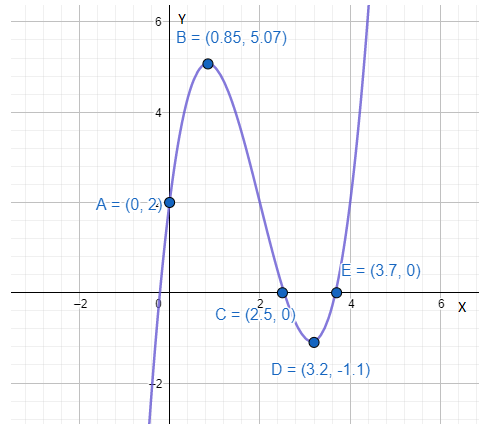
The motion of the particle can be divided into six phases
(a) The particle starts when
(b) The particle changes direction and continues its motion until at
(c) The particle stops at
(d) The particle changes direction and continues its motion until at
(e) The particle stops at
(f) Then it stops and continues its motion.
Chapter 2 Solutions
Advanced Placement Calculus Graphical Numerical Algebraic Sixth Edition High School Binding Copyright 2020
- Question 1 (Implicit differentiation). Use implicit differentiation to find Əz/Əx and Əz/ǝy. (a) x²+2y²+3z² 1 (b) ez = xyz (c) x2. y²+ z² − 2z = 4 (d) yz+xln(y) = z²arrow_forward4. The general solution of the differential equation y′′ + 2y′ + 5y = 0 isA. c1 + c2x B. c1 cos 2x + c2 sin 2x C. c1e^x cos 2x + c2e^x sin 2xD. c1e^−x cos 2x + c2e^−x sin 2x E. None of these.arrow_forward3. The general solution of the differential equation y′′ + 2y′ + y = 0 isA. c1e^−x + c2e^−x B. c1e^−x + c2e^x C. c1e^−x + c2xe^−xD. c1 cos x + c2 sin x E. c1e^−xarrow_forward
- 1. A solution to the differential equation y′′ + 4y′ + 13y = 0 isA. y(t) = e^2t cos 3t B. y(t) = te^2t cos 3t C. y(t) = e^−2t sin 3t D. None of thesearrow_forward2. The appropriate guess for the particular solution to the differential equationy′′ + 3y′ + 2y = 2x + 3e^−x isA. A + Bx + Ce^−x B. A + Bx + Cxe^−x C. Ax + Bx^2 + Ce−^x D. Ax + Bx^2 + Cxe^−xarrow_forward23. Network Analysis The figure shows the flow of traffic (in vehicles per hour) through a network of streets. 200 100- -100 200 (a) Solve this system for i = 1, 2, 3, 4. (b) Find the traffic flow when x = 0. (c) Find the traffic flow when x = 100. (d) Find the traffic flow when x, = 2x₂.arrow_forward
- 2\int_{-3/2}^{3/2} \sqrt{4u^2+2} duarrow_forward2. Consider the following: Prove that x, x2, and 1/x are the solutions to the homogeneous equation corresponding to x³y"" + x²y" + 2xy' + 2y = 2x4. b. use variation of parameters to find a particular solution and complete the general solution to the differential equation. I am interested in process. You may use a computer for integration, finding determinants and doing Kramer's.arrow_forward3. A spring is stretched 6 in. by a mass that weighs 8 lb. The mass is attached to a dashpot mechanism that has a damping constant of 0.25 lb-sec./ft. and is acted on by an external force of 4 cos 2t lb. a. Set-up the differential equation and initial value problem for the system. b. Write the function in phase-amplitude form. C. Determine the transient solution to the system. Show your work. d. Determine the steady state of this system. Show your work. e. Is the system underdamped, overdamped or critically damped? Explain what this means for the system.arrow_forward
- 4. Suppose that you have a circuit with a resistance of 20, inductance of 14 H and a capacitance of 11 F. An EMF with equation of E(t) = 6 cos 4t supplies a continuous charge 60 to the circuit. Suppose that the q(0)= 8 V and the q'(0)=7. Use this information to answer the following questions a. Find the function that models the charge of this circuit. b. Is the circuit underdamped, overdamped or critically damped?arrow_forward1. Solve the initial value problem: y" -11y' + 30y = x³e6x y(0) 11, y'(0) = 36 =arrow_forwardWhat is the particular solution to the differential equation y′′ + y = 1/cos t ?arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





