Advanced Placement Calculus Graphical Numerical Algebraic Sixth Edition High School Binding Copyright 2020
6th Edition
ISBN: 9781418300203
Author: Prentice Hall
Publisher: Prentice Hall
expand_more
expand_more
format_list_bulleted
Question
Chapter 2.1, Problem 30E
(a.)
To determine
To sketch: a graph of elevation
(a.)
Expert Solution
Answer to Problem 30E
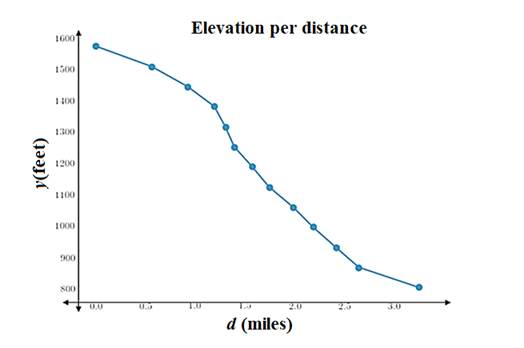
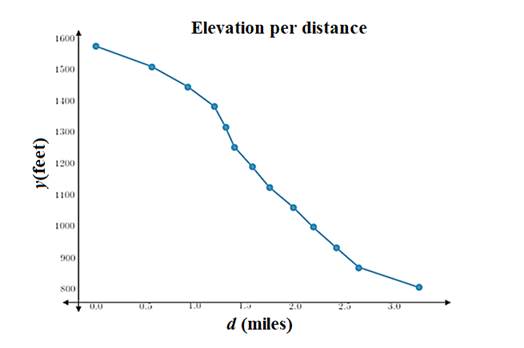
The required graph is shown.
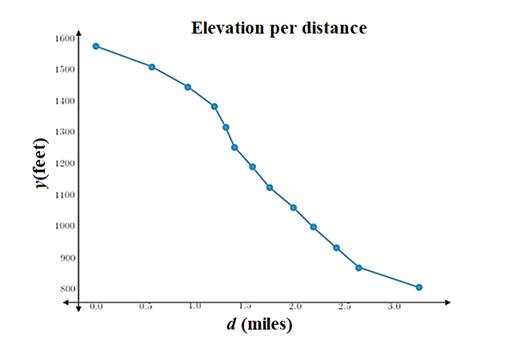
Explanation of Solution
Given:
| Elevation Along Bear Creek | |
| Distance Downriver | River Elevation |
| 0.00 | 1577 |
| 0.56 | 1512 |
| 0.92 | 1448 |
| 1.19 | 1384 |
| 1.30 | 1319 |
| 1.39 | 1255 |
| 1.57 | 1191 |
| 1.74 | 1126 |
| 1.98 | 1062 |
| 2.18 | 998 |
| 2.41 | 933 |
| 2.64 | 869 |
| 3.24 | 805 |
Calculation:
Plot the points on graph and join them
(b.)
To determine
To obtain: an approximate graph of the derivative.
(b.)
Expert Solution
Answer to Problem 30E
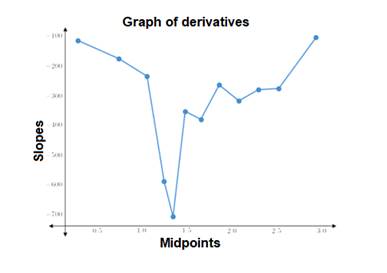
The graph of the derivative is shown.
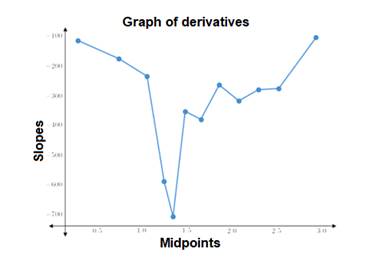
Explanation of Solution
Given:
| Elevation Along Bear Creek | |
| Distance Downriver | River Elevation |
| 0.00 | 1577 |
| 0.56 | 1512 |
| 0.92 | 1448 |
| 1.19 | 1384 |
| 1.30 | 1319 |
| 1.39 | 1255 |
| 1.57 | 1191 |
| 1.74 | 1126 |
| 1.98 | 1062 |
| 2.18 | 998 |
| 2.41 | 933 |
| 2.64 | 869 |
| 3.24 | 805 |
Concept used:
The derivative of a function is represented by slope of graph.
Calculation:
Create a table with mid point of each interval and their respective slopes.
| Elevation Along Bear Creek | |
| Distance Downriver | River Elevation |
Now plot the above points on the graph and join them.
(c.)
To determine
The units of measure would be appropriate for a gradient in this problem.
(c.)
Expert Solution
Answer to Problem 30E
The unit of gradient is feet per mile.
Explanation of Solution
Given:
| Elevation Along Bear Creek | |
| Distance Downriver (miles) | River Elevation (feet) |
| 0.00 | 1577 |
| 0.56 | 1512 |
| 0.92 | 1448 |
| 1.19 | 1384 |
| 1.30 | 1319 |
| 1.39 | 1255 |
| 1.57 | 1191 |
| 1.74 | 1126 |
| 1.98 | 1062 |
| 2.18 | 998 |
| 2.41 | 933 |
| 2.64 | 869 |
| 3.24 | 805 |
Concept used:
The average change in elevation over a given distance is called a gradient.
Conclusion:
Here, the elevation is given in feet and the distance down the river is given in miles.
Thus, the units of the gradient will be feet per mile.
(d.)
To determine
The units of measure would be appropriate for derivative.
(d.)
Expert Solution
Answer to Problem 30E
The units of the gradient will be feet per mile.
Explanation of Solution
Given:
| Elevation Along Bear Creek | |
| Distance Downriver (miles) | River Elevation (feet) |
| 0.00 | 1577 |
| 0.56 | 1512 |
| 0.92 | 1448 |
| 1.19 | 1384 |
| 1.30 | 1319 |
| 1.39 | 1255 |
| 1.57 | 1191 |
| 1.74 | 1126 |
| 1.98 | 1062 |
| 2.18 | 998 |
| 2.41 | 933 |
| 2.64 | 869 |
| 3.24 | 805 |
Concept used:
Derivative is given by the slope.
Here, the average change in elevation over a given distance is slope.
Conclusion:
Here, the elevation is given in feet and the distance down the river is given in miles.
Thus, the units of the gradient will be feet per mile.
(e)
To determine
To identify: The most dangerous section of the river by analyzing the graph in (a).
(e)
Expert Solution
Answer to Problem 30E
The most dangerous section of the river is from 1.2 to 1.5 miles.
Explanation of Solution
Given:
| Elevation Along Bear Creek | |
| Distance Downriver (miles) | River Elevation (feet) |
| 0.00 | 1577 |
| 0.56 | 1512 |
| 0.92 | 1448 |
| 1.19 | 1384 |
| 1.30 | 1319 |
| 1.39 | 1255 |
| 1.57 | 1191 |
| 1.74 | 1126 |
| 1.98 | 1062 |
| 2.18 | 998 |
| 2.41 | 933 |
| 2.64 | 869 |
| 3.24 | 805 |
Conclusion:
In the graph, the steepest part which is from 1.2 to 1.5 miles.
Chapter 2 Solutions
Advanced Placement Calculus Graphical Numerical Algebraic Sixth Edition High School Binding Copyright 2020
Ch. 2.1 - Prob. 1QRCh. 2.1 - Prob. 2QRCh. 2.1 - Prob. 3QRCh. 2.1 - Prob. 4QRCh. 2.1 - Prob. 5QRCh. 2.1 - Prob. 6QRCh. 2.1 - Prob. 7QRCh. 2.1 - Prob. 8QRCh. 2.1 - Prob. 9QRCh. 2.1 - Prob. 10QR
Ch. 2.1 - Prob. 1ECh. 2.1 - Prob. 2ECh. 2.1 - Prob. 3ECh. 2.1 - Prob. 4ECh. 2.1 - Prob. 5ECh. 2.1 - Prob. 6ECh. 2.1 - Prob. 7ECh. 2.1 - Prob. 8ECh. 2.1 - Prob. 9ECh. 2.1 - Prob. 10ECh. 2.1 - Prob. 11ECh. 2.1 - Prob. 12ECh. 2.1 - Prob. 13ECh. 2.1 - Prob. 14ECh. 2.1 - Prob. 15ECh. 2.1 - Prob. 16ECh. 2.1 - Prob. 17ECh. 2.1 - Prob. 18ECh. 2.1 - Prob. 19ECh. 2.1 - Prob. 20ECh. 2.1 - Prob. 21ECh. 2.1 - Prob. 22ECh. 2.1 - Prob. 23ECh. 2.1 - Prob. 24ECh. 2.1 - Prob. 25ECh. 2.1 - Prob. 26ECh. 2.1 - Prob. 27ECh. 2.1 - Prob. 28ECh. 2.1 - Prob. 29ECh. 2.1 - Prob. 30ECh. 2.1 - Prob. 31ECh. 2.1 - Prob. 32ECh. 2.1 - Prob. 33ECh. 2.1 - Prob. 34ECh. 2.1 - Prob. 35ECh. 2.1 - Prob. 36ECh. 2.1 - Prob. 37ECh. 2.1 - Prob. 38ECh. 2.1 - Prob. 39ECh. 2.1 - Prob. 40ECh. 2.1 - Prob. 41ECh. 2.1 - Prob. 42ECh. 2.1 - Prob. 43ECh. 2.1 - Prob. 44ECh. 2.1 - Prob. 45ECh. 2.1 - Prob. 46ECh. 2.2 - Prob. 1QRCh. 2.2 - Prob. 2QRCh. 2.2 - Prob. 3QRCh. 2.2 - Prob. 4QRCh. 2.2 - Prob. 5QRCh. 2.2 - Prob. 6QRCh. 2.2 - Prob. 7QRCh. 2.2 - Prob. 8QRCh. 2.2 - Prob. 9QRCh. 2.2 - Prob. 10QRCh. 2.2 - Prob. 1ECh. 2.2 - Prob. 2ECh. 2.2 - Prob. 3ECh. 2.2 - Prob. 4ECh. 2.2 - Prob. 5ECh. 2.2 - Prob. 6ECh. 2.2 - Prob. 7ECh. 2.2 - Prob. 8ECh. 2.2 - Prob. 9ECh. 2.2 - Prob. 10ECh. 2.2 - Prob. 11ECh. 2.2 - Prob. 12ECh. 2.2 - Prob. 13ECh. 2.2 - Prob. 14ECh. 2.2 - Prob. 15ECh. 2.2 - Prob. 16ECh. 2.2 - Prob. 17ECh. 2.2 - Prob. 18ECh. 2.2 - Prob. 19ECh. 2.2 - Prob. 20ECh. 2.2 - Prob. 21ECh. 2.2 - Prob. 22ECh. 2.2 - Prob. 23ECh. 2.2 - Prob. 24ECh. 2.2 - Prob. 25ECh. 2.2 - Prob. 26ECh. 2.2 - Prob. 27ECh. 2.2 - Prob. 28ECh. 2.2 - Prob. 29ECh. 2.2 - Prob. 30ECh. 2.2 - Prob. 31ECh. 2.2 - Prob. 32ECh. 2.2 - Prob. 33ECh. 2.2 - Prob. 34ECh. 2.2 - Prob. 35ECh. 2.2 - Prob. 36ECh. 2.2 - Prob. 37ECh. 2.2 - Prob. 38ECh. 2.2 - Prob. 39ECh. 2.2 - Prob. 40ECh. 2.2 - Prob. 41ECh. 2.2 - Prob. 42ECh. 2.2 - Prob. 43ECh. 2.2 - Prob. 44ECh. 2.2 - Prob. 45ECh. 2.2 - Prob. 46ECh. 2.2 - Prob. 47ECh. 2.2 - Prob. 48ECh. 2.3 - Prob. 1QRCh. 2.3 - Prob. 2QRCh. 2.3 - Prob. 3QRCh. 2.3 - Prob. 4QRCh. 2.3 - Prob. 5QRCh. 2.3 - Prob. 6QRCh. 2.3 - Prob. 7QRCh. 2.3 - Prob. 8QRCh. 2.3 - Prob. 9QRCh. 2.3 - Prob. 10QRCh. 2.3 - Prob. 1ECh. 2.3 - Prob. 2ECh. 2.3 - Prob. 3ECh. 2.3 - Prob. 4ECh. 2.3 - Prob. 5ECh. 2.3 - Prob. 6ECh. 2.3 - Prob. 7ECh. 2.3 - Prob. 8ECh. 2.3 - Prob. 9ECh. 2.3 - Prob. 10ECh. 2.3 - Prob. 11ECh. 2.3 - Prob. 12ECh. 2.3 - Prob. 13ECh. 2.3 - Prob. 14ECh. 2.3 - Prob. 15ECh. 2.3 - Prob. 16ECh. 2.3 - Prob. 17ECh. 2.3 - Prob. 18ECh. 2.3 - Prob. 19ECh. 2.3 - Prob. 20ECh. 2.3 - Prob. 21ECh. 2.3 - Prob. 22ECh. 2.3 - Prob. 23ECh. 2.3 - Prob. 24ECh. 2.3 - Prob. 25ECh. 2.3 - Prob. 26ECh. 2.3 - Prob. 27ECh. 2.3 - Prob. 28ECh. 2.3 - Prob. 29ECh. 2.3 - Prob. 30ECh. 2.3 - Prob. 31ECh. 2.3 - Prob. 32ECh. 2.3 - Prob. 33ECh. 2.3 - Prob. 34ECh. 2.3 - Prob. 35ECh. 2.3 - Prob. 36ECh. 2.3 - Prob. 37ECh. 2.3 - Prob. 38ECh. 2.3 - Prob. 39ECh. 2.3 - Prob. 40ECh. 2.3 - Prob. 41ECh. 2.3 - Prob. 42ECh. 2.3 - Prob. 43ECh. 2.3 - Prob. 44ECh. 2.3 - Prob. 45ECh. 2.3 - Prob. 46ECh. 2.3 - Prob. 47ECh. 2.3 - Prob. 48ECh. 2.3 - Prob. 49ECh. 2.3 - Prob. 50ECh. 2.3 - Prob. 51ECh. 2.3 - Prob. 52ECh. 2.3 - Prob. 53ECh. 2.3 - Prob. 54ECh. 2.3 - Prob. 55ECh. 2.3 - Prob. 56ECh. 2.3 - Prob. 57ECh. 2.3 - Prob. 58ECh. 2.3 - Prob. 59ECh. 2.3 - Prob. 1QQCh. 2.3 - Prob. 2QQCh. 2.3 - Prob. 3QQCh. 2.3 - Prob. 4QQCh. 2.4 - Prob. 1QRCh. 2.4 - Prob. 2QRCh. 2.4 - Prob. 3QRCh. 2.4 - Prob. 4QRCh. 2.4 - Prob. 5QRCh. 2.4 - Prob. 6QRCh. 2.4 - Prob. 7QRCh. 2.4 - Prob. 8QRCh. 2.4 - Prob. 9QRCh. 2.4 - Prob. 10QRCh. 2.4 - Prob. 1ECh. 2.4 - Prob. 2ECh. 2.4 - Prob. 3ECh. 2.4 - Prob. 4ECh. 2.4 - Prob. 5ECh. 2.4 - Prob. 6ECh. 2.4 - Prob. 7ECh. 2.4 - Prob. 8ECh. 2.4 - Prob. 9ECh. 2.4 - Prob. 10ECh. 2.4 - Prob. 11ECh. 2.4 - Prob. 12ECh. 2.4 - Prob. 13ECh. 2.4 - Prob. 14ECh. 2.4 - Prob. 15ECh. 2.4 - Prob. 16ECh. 2.4 - Prob. 17ECh. 2.4 - Prob. 18ECh. 2.4 - Prob. 19ECh. 2.4 - Prob. 20ECh. 2.4 - Prob. 21ECh. 2.4 - Prob. 22ECh. 2.4 - Prob. 23ECh. 2.4 - Prob. 24ECh. 2.4 - Prob. 25ECh. 2.4 - Prob. 26ECh. 2.4 - Prob. 27ECh. 2.4 - Prob. 28ECh. 2.4 - Prob. 29ECh. 2.4 - Prob. 30ECh. 2.4 - Prob. 31ECh. 2.4 - Prob. 32ECh. 2.4 - Prob. 33ECh. 2.4 - Prob. 34ECh. 2.4 - Prob. 35ECh. 2.4 - Prob. 36ECh. 2.4 - Prob. 37ECh. 2.4 - Prob. 38ECh. 2.4 - Prob. 39ECh. 2.4 - Prob. 40ECh. 2.4 - Prob. 41ECh. 2.4 - Prob. 42ECh. 2.4 - Prob. 43ECh. 2.4 - Prob. 44ECh. 2.4 - Prob. 45ECh. 2.4 - Prob. 46ECh. 2.4 - Prob. 47ECh. 2.4 - Prob. 48ECh. 2.4 - Prob. 49ECh. 2.4 - Prob. 50ECh. 2.5 - Prob. 1QRCh. 2.5 - Prob. 2QRCh. 2.5 - Prob. 3QRCh. 2.5 - Prob. 4QRCh. 2.5 - Prob. 5QRCh. 2.5 - Prob. 6QRCh. 2.5 - Prob. 7QRCh. 2.5 - Prob. 8QRCh. 2.5 - Prob. 9QRCh. 2.5 - Prob. 10QRCh. 2.5 - Prob. 1ECh. 2.5 - Prob. 2ECh. 2.5 - Prob. 3ECh. 2.5 - Prob. 4ECh. 2.5 - Prob. 5ECh. 2.5 - Prob. 6ECh. 2.5 - Prob. 7ECh. 2.5 - Prob. 8ECh. 2.5 - Prob. 9ECh. 2.5 - Prob. 10ECh. 2.5 - Prob. 11ECh. 2.5 - Prob. 12ECh. 2.5 - Prob. 13ECh. 2.5 - Prob. 14ECh. 2.5 - Prob. 15ECh. 2.5 - Prob. 16ECh. 2.5 - Prob. 17ECh. 2.5 - Prob. 18ECh. 2.5 - Prob. 19ECh. 2.5 - Prob. 20ECh. 2.5 - Prob. 21ECh. 2.5 - Prob. 22ECh. 2.5 - Prob. 23ECh. 2.5 - Prob. 24ECh. 2.5 - Prob. 25ECh. 2.5 - Prob. 26ECh. 2.5 - Prob. 27ECh. 2.5 - Prob. 28ECh. 2.5 - Prob. 29ECh. 2.5 - Prob. 30ECh. 2.5 - Prob. 31ECh. 2.5 - Prob. 32ECh. 2.5 - Prob. 33ECh. 2.5 - Prob. 34ECh. 2.5 - Prob. 35ECh. 2.5 - Prob. 36ECh. 2.5 - Prob. 37ECh. 2.5 - Prob. 38ECh. 2.5 - Prob. 39ECh. 2.5 - Prob. 40ECh. 2.5 - Prob. 41ECh. 2.5 - Prob. 42ECh. 2.5 - Prob. 43ECh. 2.5 - Prob. 44ECh. 2.5 - Prob. 45ECh. 2.5 - Prob. 46ECh. 2.5 - Prob. 47ECh. 2.5 - Prob. 48ECh. 2.5 - Prob. 49ECh. 2.5 - Prob. 50ECh. 2.5 - Prob. 51ECh. 2.5 - Prob. 52ECh. 2.5 - Prob. 1QQCh. 2.5 - Prob. 2QQCh. 2.5 - Prob. 3QQCh. 2.5 - Prob. 4QQCh. 2 - Prob. 1RWDTCh. 2 - Prob. 2RWDTCh. 2 - Prob. 3RWDTCh. 2 - Prob. 4RWDTCh. 2 - Prob. 5RWDTCh. 2 - Prob. 6RWDTCh. 2 - Prob. 7RWDTCh. 2 - Prob. 8RWDTCh. 2 - Prob. 9RWDTCh. 2 - Prob. 10RWDTCh. 2 - Prob. 1RECh. 2 - Prob. 2RECh. 2 - Prob. 3RECh. 2 - Prob. 4RECh. 2 - Prob. 5RECh. 2 - Prob. 6RECh. 2 - Prob. 7RECh. 2 - Prob. 8RECh. 2 - Prob. 9RECh. 2 - Prob. 10RECh. 2 - Prob. 11RECh. 2 - Prob. 12RECh. 2 - Prob. 13RECh. 2 - Prob. 14RECh. 2 - Prob. 15RECh. 2 - Prob. 16RECh. 2 - Prob. 17RECh. 2 - Prob. 18RECh. 2 - Prob. 19RECh. 2 - Prob. 20RECh. 2 - Prob. 21RECh. 2 - Prob. 22RECh. 2 - Prob. 23RECh. 2 - Prob. 24RECh. 2 - Prob. 25RECh. 2 - Prob. 26RECh. 2 - Prob. 27RECh. 2 - Prob. 28RECh. 2 - Prob. 29RECh. 2 - Prob. 30RECh. 2 - Prob. 31RECh. 2 - Prob. 32RECh. 2 - Prob. 33RECh. 2 - Prob. 34RECh. 2 - Prob. 35RECh. 2 - Prob. 36RECh. 2 - Prob. 37RECh. 2 - Prob. 38RECh. 2 - Prob. 39RECh. 2 - Prob. 40RECh. 2 - Prob. 41RECh. 2 - Prob. 42RECh. 2 - Prob. 43RECh. 2 - Prob. 44RECh. 2 - Prob. 45RECh. 2 - Prob. 46RECh. 2 - Prob. 47RECh. 2 - Prob. 48RECh. 2 - Prob. 49RECh. 2 - Prob. 50RECh. 2 - Prob. 51RECh. 2 - Prob. 52RECh. 2 - Prob. 53RECh. 2 - Prob. 54RECh. 2 - Prob. 55RECh. 2 - Prob. 56RECh. 2 - Prob. 57RECh. 2 - Prob. 58RECh. 2 - Prob. 59RECh. 2 - Prob. 60RECh. 2 - Prob. 61RECh. 2 - Prob. 62RECh. 2 - Prob. 63RECh. 2 - Prob. 64RECh. 2 - Prob. 65RECh. 2 - Prob. 66RECh. 2 - Prob. 67RECh. 2 - Prob. 68RECh. 2 - Prob. 69RECh. 2 - Prob. 70RECh. 2 - Prob. 71RECh. 2 - Prob. 72RECh. 2 - Prob. 73RECh. 2 - Prob. 74RECh. 2 - Prob. 75RECh. 2 - Prob. 76RECh. 2 - Prob. 77RECh. 2 - Prob. 78RECh. 2 - Prob. 79RECh. 2 - Prob. 80RECh. 2 - Prob. 81EPCh. 2 - Prob. 82EPCh. 2 - Prob. 83EP
Knowledge Booster
Similar questions
- Do the Laplace Transformation and give the answer in Partial Fractions. Also do the Inverted Laplace Transformation and explain step-by-step.arrow_forward12. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.508.XP. ASK YOUR TEA Make a substitution to express the integrand as a rational function and then evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) x + 16 dx X Need Help? Read It SUBMIT ANSWER 13. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.512.XP. ASK YOUR TEA Make a substitution to express the integrand as a rational function and then evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) dx 8)(2x + 1) Need Help? Read It SUBMIT ANSWER 14. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.518.XP. Find the area of the region under the given curve from 1 to 5. y = x² +7 6x - x² Need Help? Read It ASK YOUR TEAarrow_forwardDETAILS MY NOTES SESSCALCET2 6.3.012. 6. [-/1 Points] Evaluate the integral. x-4 dx x² - 5x + 6 Need Help? Read It SUBMIT ANSWER 7. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.019. Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) x²+1 (x-6)(x-5)² dx Need Help? Read It SUBMIT ANSWER 8. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.021. Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) ✓ x² 4 +4 dxarrow_forward
- DETAILS MY NOTES SESSCALCET2 6.3.017. 1. [-/1 Points] Evaluate the integral. - - dy y(y + 2)(y-3) Need Help? Read It Watch It SUBMIT ANSWER 2. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.027. Evaluate the integral. (Use C for the constant of integration.) X + 16 x²+10x29 dx Need Help? Read It Watch It SUBMIT ANSWERarrow_forwardDo the Laplace Transformation for this equation in Partial Fractions.arrow_forwardUse undetermined coefficients to find the particular solution to y"-2y-4y=3t+6 Yp(t) =arrow_forward
- Car A starts from rest at t = 0 and travels along a straight road with a constant acceleration of 6 ft/s^2 until it reaches a speed of 60ft/s. Afterwards it maintains the speed. Also, when t = 0, car B located 6000 ft down the road is traveling towards A at a constant speed of 80 ft/s. Determine the distance traveled by Car A when they pass each other.Write the solution using pen and draw the graph if needed.arrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forward
- 4. Use method of separation of variable to solve the following wave equation მłu J²u subject to u(0,t) =0, for t> 0, u(л,t) = 0, for t> 0, = t> 0, at² ax²' u(x, 0) = 0, 0.01 x, ut(x, 0) = Π 0.01 (π-x), 0arrow_forwardSolve the following heat equation by method of separation variables: ди = at subject to u(0,t) =0, for -16024 ძx2 • t>0, 0 0, ux (4,t) = 0, for t> 0, u(x, 0) = (x-3, \-1, 0 < x ≤2 2≤ x ≤ 4.arrow_forwardex 5. important aspects. Graph f(x)=lnx. Be sure to make your graph big enough to easily read (use the space given.) Label all 6 33arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning