Physics for Scientists and Engineers with Modern Physics
10th Edition
ISBN: 9781337553292
Author: Raymond A. Serway, John W. Jewett
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 23, Problem 1P
A negatively charged rod of finite length carries charge with a uniform charge per unit length. Sketch the electric field lines in a plane containing the rod.
Expert Solution & Answer
To determine
To draw: The electric field lines in a plane containing the rod.
Answer to Problem 1P
The diagram of electric field lines in a plane containing the rod is
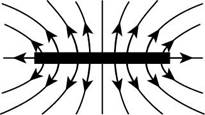
Figure (1)
Explanation of Solution
Introduction:
Field lines represent a uniform electric field penetrating a plane of the area perpendicular to the field. The electric field is a vector field around a charged particle. It represents the force that other charged particles would feel if placed near the particle creating the electric field.
If the charge is positive, field lines points radially away from the rod; if the charge is negative, field lines points radially towards the rod. As the charge is negative, the field lines points radially towards the rod.
The diagram below shows the electric field lines in a plane containing the rod
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
Consider a charge configuration comprising two point sources, one carrying a positive charge and the other a negative charge. The magnitude of the negative charge is three times as large as the positive charge. Construct a careful sketch of the electric field around the configuration.
A charged metal sphere of radius Rs and a charged, flat metal disk of radius Rp are connected by a long conducting wire.
The sphere has a charge Qs (assume it is uniformly distributed on its surface).
What is Qp, the charge on the disk (assume it is uniformly distributed on its surface)?
Give your answer in nC to at least three digits to avoid being counted off due to rounding.
Rs = 0.40 m, Rp = 0.33 m, Qs = 29.3 nC
Sphere
Qs, Rs
2D Disk
QD, RD
A uniformly charged rod of length L = 1.2 m lies along the x-axis with its right end at the origin. The rod has a total charge of Q = 6.8 μC. A point P is located on the x-axis a distance a = 2.4 m to the right of the origin.Integrate the electric field contributions from each slice over the length of the rod to write an equation for the net electric field E at point P.
Chapter 23 Solutions
Physics for Scientists and Engineers with Modern Physics
Ch. 23.2 - Suppose a point charge is located at the center of...Ch. 23.3 - If the net flux through a gaussian surface is...Ch. 23 - A negatively charged rod of finite length carries...Ch. 23 - A positively charged disk has a uniform charge per...Ch. 23 - A uniformly charged ring of radius 10.0 cm has a...Ch. 23 - The electric field along the axis of a uniformly...Ch. 23 - Example 23.3 derives the exact expression for the...Ch. 23 - A uniformly charged rod of length L and total...Ch. 23 - A continuous line of charge lies along the x axis,...Ch. 23 - A thin rod of length and uniform charge per unit...
Ch. 23 - (a) Consider a uniformly charged, thin-walled,...Ch. 23 - A vertical electric field of magnitude 2.00 104...Ch. 23 - A flat surface of area 3.20 m2 is rotated in a...Ch. 23 - A nonuniform electric field is given by the...Ch. 23 - An uncharged, nonconducting, hollow sphere of...Ch. 23 - Find the net electric flux through the spherical...Ch. 23 - Four closed surfaces, S1 through S4 together with...Ch. 23 - A charge of 170 C is at the center of a cube of...Ch. 23 - (a) Find the net electric flux through the cube...Ch. 23 - A particle with charge of 12.0 C is placed at the...Ch. 23 - A particle with charge Q = 5.00 C is located at...Ch. 23 - Prob. 20PCh. 23 - Prob. 21PCh. 23 - Find the net electric flux through (a) the closed...Ch. 23 - Figure P23.23 represents the top view of a cubic...Ch. 23 - Determine the magnitude of the electric field at...Ch. 23 - Prob. 25PCh. 23 - Prob. 26PCh. 23 - A large, flat, horizontal sheet of charge has a...Ch. 23 - A nonconducting wall carries charge with a uniform...Ch. 23 - A uniformly charged, straight filament 7.00 m in...Ch. 23 - You are working on a laboratory device that...Ch. 23 - Consider a long, cylindrical charge distribution...Ch. 23 - Assume the magnitude of the electric field on each...Ch. 23 - A solid sphere of radius 40.0 cm has a total...Ch. 23 - A cylindrical shell of radius 7.00 cm and length...Ch. 23 - You are working for the summer at a research...Ch. 23 - You are working for the summer at a research...Ch. 23 - Find the electric flux through the plane surface...Ch. 23 - Prob. 38APCh. 23 - Prob. 39APCh. 23 - Show that the maximum magnitude Emax of the...Ch. 23 - A line of positive charge is formed into a...Ch. 23 - Prob. 42APCh. 23 - A sphere of radius R = 1.00 m surrounds a particle...Ch. 23 - A sphere of radius R surrounds a particle with...Ch. 23 - A slab of insulating material has a nonuniform...Ch. 23 - A sphere of radius 2a is made of a nonconducting...Ch. 23 - Prob. 47CPCh. 23 - Prob. 48CPCh. 23 - Review. A slab of insulating material (infinite in...Ch. 23 - Identical thin rods of length 2a carry equal...Ch. 23 - A solid insulating sphere of radius R has a...
Additional Science Textbook Solutions
Find more solutions based on key concepts
1. Rub your hands together vigorously. What happens? Discuss the energy transfers and transformations that take...
College Physics: A Strategic Approach (4th Edition)
Scientific Method.
Glencoe Physics: Principles and Problems, Student Edition
Monochromatic light from a distant point source is incident on two slits. The resulting graph of intensity vers...
Tutorials in Introductory Physics
Check Your Understanding If the line spacing of a diffraction grating d is not precisely known, we can use a li...
University Physics Volume 3
Is Earths inner core solid and the outer core liquid because the inner core is cooler than the outer core? Expl...
Conceptual Integrated Science
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Consider a thin, spherical shell of radius 14.0 cm with a total charge of 32.0 C distributed uniformly on its surface. Find the electric field (a) 10.0 cm and (b) 20.0 cm from the center of the charge distribution.arrow_forwardThe electric field at a point on the perpendicular bisector of a charged rod was calculated as the first example of a continuous charge distribution, resulting in Equation 24.15:E=kQy12+y2j a. Find an expression for the electric field when the rod is infinitely long. b. An infinitely long rod with uniform linear charge density also contains an infinite amount of charge. Explain why this still produces an electric field near the rod that is finite.arrow_forwardA metal sphere of radius 10 cm carries a charge of +2 μC uniformly distributed over its surface. What is the magnitude of the electric field due to this sphere at a point 5 cm outside the sphere’s surface?arrow_forward
- A positively charged line with linear charge density λ is pictured along the x-axis with length L. Starting with the differential form of Coulomb’s Law () derive an equation for the electric field at point P at (x=a, y=0) k, a, L, and λ.arrow_forwardWhat is the magnitude and direction of the electric field at 0.25 m from a -5.6 x10-6 C point charge? A proton is released from rest in a uniform horizontal electric field. It travels 3.25 m for 5 us. Find the acceleration of the proton and the magnitude of the electric field. A solid insulating sphere of radius 0.07 m carries a total charge of 25µC. Concentric with this sphere is a conducting spherical shell of inner radius 0.12 m and outer radius of 0.18 m and carrying a total charge of -54 µC. Find (a) the charge distribution for the insulating sphere and the conducting spherical shell, and the magnitude of the electric field at the following distances from the center of the two spheres and shell: (b) 0.05 m, (c) 0.10 m, (d) 0.15 m, and (e) 0.25 m.arrow_forwardA very thin spherical shell of radius a has a total charge of Q distributed uniformly over its surface . Find the electric field at points inside and outside the shell.arrow_forward
- The figure below shows three circular arcs centered on the origin of a coordinate system. On each arc, the uniformly distributed charge is given in terms of Q = 6.00 μC. The radii are given in terms of R = 12.0 cm. (a) What is the magnitude of the net electric field at the origin due to the arcs? ______N/C(b) What is the direction of the field (relative to the positive x direction)?_______ ° counterclockwise from the +x-axis (please include units in your explanations so that I can follow easier)arrow_forwardA point charge Q of -9.86 C and a large flat plate with surface charge density 2.15 C/m2 together create an electric field 5.03 m from the plate. Point P is a distance b = 9.25 m from at point P. Charge Q and point P are each a distance a = charge Q. Find the magnitude of the force exerted by the electric field on a particle with charge 4.54 nC placed at point P in the figure. Answer in units of N. plate (side view)arrow_forwardA thin rod of length L=6.7 m carries a uniform charge q=6.1 μC along its length. Take Coulomb's constant as k=9 x 109 N m2 / C2. Determine the magnitude of the electric field at point A. Express your answer using 1 decimal place without entering the units.arrow_forward
- A uniformly charged rod of length L lies along the x-axis with its right end at the origin. The rod has a total charge of Q. A point P is located on the x-axis a distance a to the right of the origin. Write an equation for the electric field dE at point P due to the thin slice of the rod dx. Give the answer is terms of the variables Q, L, x, a, dx, and coulombs constant k. Integrate the electric field contributions from each slice over the length of the rod to write an equation for the net electric field E at point P. Calculate the magnitude of the electric field E in kilonewtons per coulomb (kN/C) at point P due to the charged rod if L = 2.2m, Q = 8.5 μC and a = 1.1m.arrow_forwardConsider the semicircular ring of charge shown in the figure. The total charge of the ring is 2.5 μC and the radius of the ring is 0.45 m. a) What is the magnitude of the electric field, in newtons per coulomb, at point P, in the center of the semicircle?arrow_forwardSuppose there are two uniformly charged non-conducting spheres, one with a charge +Q, the other of charge -Q, each with radius R. The centres of these spheres are separated by a distance z = 3R. Draw a diagram indicating this, and show the positions where the electric field is equal to zero.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Electric Fields: Crash Course Physics #26; Author: CrashCourse;https://www.youtube.com/watch?v=mdulzEfQXDE;License: Standard YouTube License, CC-BY