Chapter 2.2, Problem 90E

To determine

To find: The sketch for the graph of the function, and approximate the root feature to approximate the real zeroes of the function.

Answer to Problem 90E

Thesketch for the graph is shown in Figure 11 and thezero at $x=0$ is of multiplicity $2$ and the other zero is at $x=\pm 2\sqrt{2}$ is of multiplicity 1.

Explanation of Solution

Given:

The given polynomial function is $f\left(x\right)=\frac{1}{4}{x}^4-2x^2$ .

Calculation:

The graph for $f\left(x\right)=\frac{1}{4}{x}^4-2x^2$ has to be graphed using the graphical utility function.

The first step is to on the calculator and press Y= button to access the Y= editor.

The required display is shown in Figure 1

  

Figure 1

The second step is to set the range by pressing the Window, it is to be noted that there should be the negative sign with the window at the start of the expression comes from minus sign of the bracket that is to the left of the ENTER button.

The required display is shown in Figure 2

  

Figure 2

The third step is to press graph.

The required display for the graph is shown in Figure 3

  

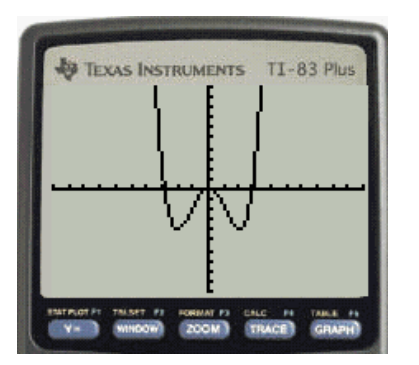
Figure 3

The fourth step is to Press TRACE to determine the x intercepts if the graph.

The required display for the graph is shown in Figure 4

  

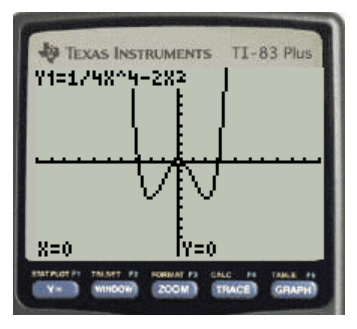
Figure 4

The fifth step is to Press the yellow coloured key to the find the graph functions and then select ZERO in the second line followed by ENTER press.

The required display for the graph is shown in Figure 5

  

Figure 5

The step six is that graph is displayed with the left bound at the bottom left coroner press the arrow key or the enter value to select the x value for the left bound of the interval then press enter.

The required display for the graph is shown in Figure 5

  

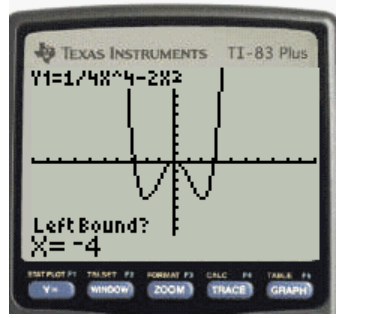
Figure 6

The step seven is that If the graph is displayed with the right bound in the bottom left then press the arrow key to select the value of the right bound of the interval and then press enter.

The required display for the graph is shown in Figure 7

  

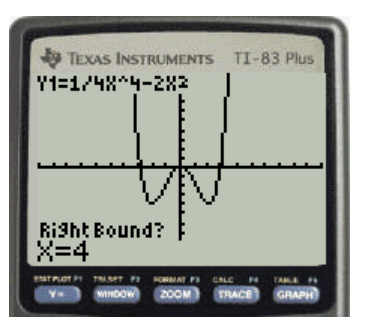
Figure 7

The step eight is that If the graph is displayed with the Guess at the bottom left corner than press the arrow key or the enter value to select the point near the zero of the function, that is between the bounds and then press enter.

The required display for the graph is shown in Figure 8

  

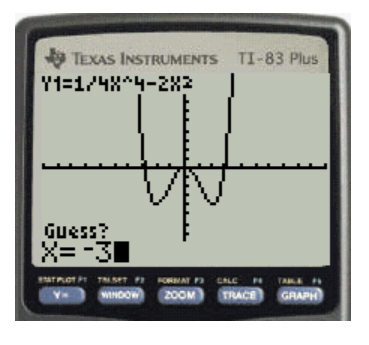
Figure 8

The step nine is that the x axis intercept nearest to the value of the guess is displayed with the coordinate. Therefore the x intercept is at $x=-2.828$ .

The required display is shown below.

  

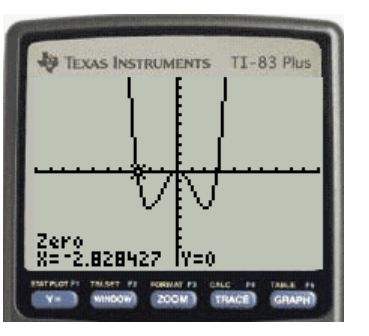
Figure 9

The step ten is to repeat from step five to eight and with the guess for the other value of the x axis intercept and the another x intercept is $x=0$ .

The required display is shown below.

  

Figure 10

The step eleven is to repeat from step five to eight and with the guess for the other value of the x axis intercept and another x intercept is $x=2.828$ .

The required Figure is shown in Figure 11

  

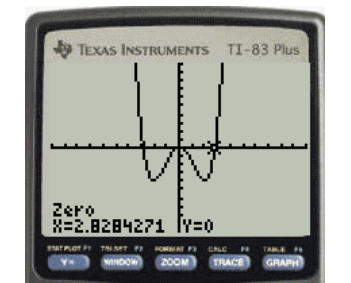
Figure 1

The graph touches the x axis at $x=0$ and it intersects the x axis at $x=-2.82,2.82$ . The value of zero at $x=0$ is of even multiplicity and zero at $x=-2.82,2.82$ is of odd multiplicity.

Then, the multiplicity of zero is,

  $\begin{array}{l}\frac{1}{4}{x}^4-2x^3=0\\ x=0,\pm 2\sqrt{2}\end{array}$