
Concept explainers
a.
The magnitude and the direction of the electric field at
The electric field
Given:
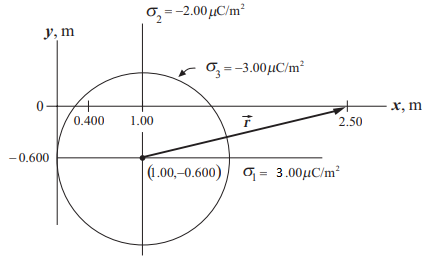
The charges are placed as shown in the figure. The first plane at
The surface charge densities are
Formula Used:
Electric field
E is the electric field.
The resultant electric field at point is
Calculations:
The resultant electric field at point is
Electric field at point 1 due to sphere.
As the point is inside the sphere the electric field is zero.
Electric field at point 1 due to plane 1
Substituting values
The electric field at point 1 due to plane 2.
Substituting in the equation
The resultant electric field at point is
Substituting
The magnitude of the electric field is
Direction:
Conclusion:
The electric field
b.
The magnitude and the direction of the electric field at
The electric field
Given:
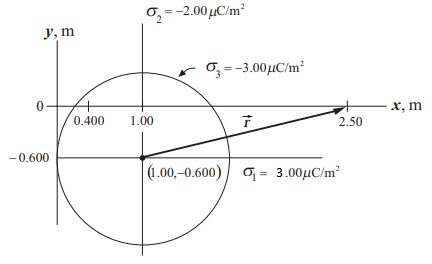
The charges are placed as shown in the figure. The first plane at
The surface charge densities are
Formula Used:
Electric field
E is the electric field.
The resultant electric field at point is
Calculations:
The resultant electric field at point is
Electric field at point 1 due to sphere.
Where
Electric field at point 1 due to plane 1
Substituting values in the formula
The electric field at point 1 due to plane 2.
Substituting in the equation
The resultant electric field at point is
Substituting
The magnitude of the electric field is
Direction:
Conclusion:
The electric field
a.
Answer to Problem 77P
The electric field
Explanation of Solution
Given:

The charges are placed as shown in the figure. The first plane at
The surface charge densities are
Formula Used:
Electric field
E is the electric field.
The resultant electric field at point is
Calculations:
The resultant electric field at point is
Electric field at point 1 due to sphere.
As the point is inside the sphere the electric field is zero.
Electric field at point 1 due to plane 1
Substituting values
The electric field at point 1 due to plane 2.
Substituting in the equation
The resultant electric field at point is
Substituting
The magnitude of the electric field is
Direction:
Conclusion:
The electric field
b.
The magnitude and the direction of the electric field at
The electric field
Given:

The charges are placed as shown in the figure. The first plane at
The surface charge densities are
Formula Used:
Electric field
E is the electric field.
The resultant electric field at point is
Calculations:
The resultant electric field at point is
Electric field at point 1 due to sphere.
Where
Electric field at point 1 due to plane 1
Substituting values in the formula
The electric field at point 1 due to plane 2.
Substituting in the equation
The resultant electric field at point is
Substituting
The magnitude of the electric field is
Direction:
Conclusion:
The electric field
b.
Answer to Problem 77P
The electric field
Explanation of Solution
Given:

The charges are placed as shown in the figure. The first plane at
The surface charge densities are
Formula Used:
Electric field
E is the electric field.
The resultant electric field at point is
Calculations:
The resultant electric field at point is
Electric field at point 1 due to sphere.
Where
Electric field at point 1 due to plane 1
Substituting values in the formula
The electric field at point 1 due to plane 2.
Substituting in the equation
The resultant electric field at point is
Substituting
The magnitude of the electric field is
Direction:
Conclusion:
The electric field
Want to see more full solutions like this?
Chapter 22 Solutions
Physics for Scientists and Engineers
- Diamond has an index of refraction of about 2.4. Suppose you cut a diamond so it has a flat surface, and shine a laser pointer beam so that it makes a 27 degree angle with respect to the normal line to that surface. What angle will the laser beam make with respect to the normal after it passes through the air-diamond boundary and is inside the diamond? Give your answer as the number of degrees.arrow_forwardFind current of each line of D,E, and F. Where V1 is 9V, V2 is 7V, R1 is 989 , R2 is 2160, R3 is 4630 , R4 is 5530, R5 is 6720, and E is 16V. Please explain all steps. Thank youarrow_forwardYou are tasked with designing a parallel-plate capacitor using two square metal plates, eachwith an area of 0.5 m², separated by a 0.1 mm thick layer of air. However, to increase the capacitance,you decide to insert a dielectric material with a dielectric constant κ = 3.0 between the plates. Describewhat happens (and why) to the E field between the plates when the dielectric is added in place of theair.arrow_forward
- Calculate the work required to assemble a uniform charge Q on a thin spherical shell of radiusR. Start with no charge and add infinitesimal charges dq until the total charge reaches Q, assuming thecharge is always evenly distributed over the shell’s surface. Show all steps.arrow_forwardRod AB is fixed to a smooth collar D, which slides freely along the vertical guide shown in (Figure 1). Point C is located just to the left of the concentrated load P = 70 lb. Suppose that w= 17 lb/ft. Follow the sign convention. Part A Figure 3 ft -1.5 ft √30° 1 of 1 Determine the normal force at point C. Express your answer in pounds to three significant figures. ΜΕ ΑΣΦ Η vec Nc= Submit Request Answer Part B Determine the shear force at point C. Express your answer in pounds to three significant figures. VC= ΜΕ ΑΣΦΗ vec Submit Request Answer Part C Determine the moment at point C. Express your answer in pound-feet to three significant figures. Mc= Ο ΑΣΦ Η vec Submit Request Answer Provide Feedback ? ? lb lb ? lb-ftarrow_forwardConsider a uniformly charged ring of radius R with total charge Q, centered at the origin inthe xy-plane. Find the electric field (as a vector) at a point on the z-axis at a distance z above thecenter of the ring. Assume the charge density is constant along the ring.arrow_forward
- 3) If the slider block C is moving at 3m/s, determine the angular velocity of BC and the crank AB at the instant shown. (Use equation Vs Vc wx fuc, then use equation Vs VA + Ve/athen write it in terms of w and the appropriate r equate the two and solve) 0.5 m B 1 m 60° A 45° vc = 3 m/sarrow_forward3) If the slider block C is moving at 3m/s, determine the angular velocity of BC and the crank AB at the instant shown. (Use equation Vs Vc wxf, then use equation V, VA + Va/Athen write it in terms of w and the appropriate r equate the two and solve) f-3marrow_forwardPls help ASAParrow_forward
- Pls help ASAParrow_forward14. A boy is out walking his dog. From his house, he walks 30 m North, then 23 m East, then 120 cm South, then 95 m West, and finally 10 m East. Draw a diagram showing the path that the boy walked, his total displacement, and then determine the magnitude and direction of his total displacement.arrow_forwardPls help ASAParrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





