
Concept explainers
(a)
The electric field between the two parallel metal plates.
(a)
Explanation of Solution
Given:
Area of the two plates is
Separation between the plates is
The amount of charge that is transfer from left plate to the right is
Formula used:
Draw a diagram to show the surface charge density of the two metal parallel plates 1 and 2.
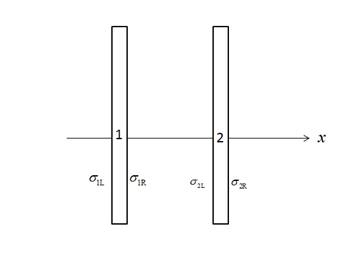
Write the expression of electric field due to a plane surface.
Here,
Write the expression for the surface charge density due to the plane 1.
Here,
Write the expression for the surface charge density due to the plane 2.
Here,
Calculation:
The electric field at a distance
Here,
Substitute
Charge of the plates is equal but opposite sue to the transfer of charges from one plate to another.
Substitute
Substitute
Here,
Substitute
Conclusion:
Thus, the electric field is
(b)
The electric field between the two parallel metal plates.
(b)
Explanation of Solution
Given:
Area of the two plates is
Separation between the plates is
The amount of charge that is transfer from left plate to the right is
Formula used:
Write the expression of electric field due to a plane surface.
Here,
Write the expression for the surface charge density due to the plane 1.
Here,
Write the expression for the surface charge density due to the plane 2.
Here,
Calculation:
The electric field at a distance
Here,
Substitute
Charge of the plates is equal but opposite sue to the transfer of charges from one plate to another.
Substitute
Substitute
Here,
Substitute
Conclusion:
Thus, the electric field is
(c)
The electric field to the left of the left plate.
(c)
Explanation of Solution
Given:
Area of the two plates is
Separation between the plates is
The amount of charge that is transfer from left plate to the right is
Formula used:
Write the expression of electric field due to a plane surface.
Here,
Write the expression for the surface charge density due to the plane 1.
Here,
Write the expression for the surface charge density due to the plane 2.
Here,
Calculation:
The electric field to the left from the plate on left.
Here,
Substitute
Charge of the plates is equal but opposite sue to the transfer of charges from one plate to another.
Substitute
Conclusion:
Thus, the electric field is
(d)
The electric field to the right of the right plate.
(d)
Explanation of Solution
Given:
Area of the two plates is
Separation between the plates is
The amount of charge that is transfer from left plate to the right is
Formula used:
Write the expression of electric field due to a plane surface.
Here,
Write the expression for the surface charge density due to the plane 1.
Here,
Write the expression for the surface charge density due to the plane 2.
Here,
Calculation:
The electric field to the right from the plate on right.
Here,
Substitute
Charge of the plates is equal but opposite sue to the transfer of charges from one plate to another.
Substitute
Conclusion:
Thus, the electric field is
Want to see more full solutions like this?
Chapter 22 Solutions
Physics for Scientists and Engineers
- Three slits, each separated from its neighbor by d = 0.06 mm, are illuminated by a coherent light source of wavelength 550 nm. The slits are extremely narrow. A screen is located L = 2.5 m from the slits. The intensity on the centerline is 0.05 W. Consider a location on the screen x = 1.72 cm from the centerline. a) Draw the phasors, according to the phasor model for the addition of harmonic waves, appropriate for this location. b) From the phasor diagram, calculate the intensity of light at this location.arrow_forwardA Jamin interferometer is a device for measuring or for comparing the indices of refraction of gases. A beam of monochromatic light is split into two parts, each of which is directed along the axis of a separate cylindrical tube before being recombined into a single beam that is viewed through a telescope. Suppose we are given the following, • Length of each tube is L = 0.4 m. • λ= 598 nm. Both tubes are initially evacuated, and constructive interference is observed in the center of the field of view. As air is slowly let into one of the tubes, the central field of view changes dark and back to bright a total of 198 times. (a) What is the index of refraction for air? (b) If the fringes can be counted to ±0.25 fringe, where one fringe is equivalent to one complete cycle of intensity variation at the center of the field of view, to what accuracy can the index of refraction of air be determined by this experiment?arrow_forward1. An arrangement of three charges is shown below where q₁ = 1.6 × 10-19 C, q2 = -1.6×10-19 C, and q3 3.2 x 10-19 C. 2 cm Y 93 92 91 X 3 cm (a) Calculate the magnitude and direction of the net force on q₁. (b) Sketch the direction of the forces on qiarrow_forward
- (Figure 1)In each case let w be the weight of the suspended crate full of priceless art objects. The strut is uniform and also has weight w Find the direction of the force exerted on the strut by the pivot in the arrangement (a). Express your answer in degrees. Find the tension Tb in the cable in the arrangement (b). Express your answer in terms of w. Find the magnitude of the force exerted on the strut by the pivot in the arrangement (b). Express your answer in terms of w.arrow_forward(Figure 1)In each case let ww be the weight of the suspended crate full of priceless art objects. The strut is uniform and also has weight w. Find the direction of the force exerted on the strut by the pivot in the arrangement (b). Express your answer in degrees.arrow_forwardA 70.0 cm, uniform, 40.0 N shelf is supported horizontally by two vertical wires attached to the sloping ceiling (Figure 1). A very small 20.0 N tool is placed on the shelf midway between the points where the wires are attached to it. Find the tension in the left-hand wire. Express your answer with the appropriate units.arrow_forward
- Find the total bind Mev. binding energy for 13 Carbon, 6C (atomic mass = 13.0033554)arrow_forwardWhat is the 27 energy absorbed in this endothermic Auclear reaction 2] Al + 'n → 27 Mg + ! H? (The atom mass of "Al is 26.981539u. and that of 11 Mg is 26.984341u) MeVarrow_forwardWhat is the energy released in this nuclear reaction 1 F + "', H-1 O+ He? 19 19 16 (The atomic mass of 1F is 18.998403 u, and that of 20 is 15.9949154) MeV.arrow_forward
- What is the energy released in this B+ nuclear reaction خالد 2½ Al w/ Mg + ie? (The atomic mass of 11 Al is 23.9999394 and that > of 12 Mg is 23.985041 u) MeV.arrow_forwardWhat is the energy released / absorbed in this nuclear reaction 14 N+ & He → » O + ! N? (The atomic mass of 14 N is 14.003074u. 17N+ and that of 10 is 16.9991324). MeVarrow_forwardCan someone help me answer this question thanks.arrow_forward

 Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





