
At point A in a Carnot cycle, 2.34 mol of a monatomic ideal gas has a pressure of 1 4000 kPa, a volume of 10.0 L, and a temperature of 720 K. The gas expands isothermally to point B and then expands adiabatically to point C, where its volume is 24.0 L. An isothermal compression brings it to point D, where its volume is 15.0 L. An adiabatic process returns the gas to point A. (a) Determine all the unknown pressures, volumes, and temperatures as you f ill in the following table:
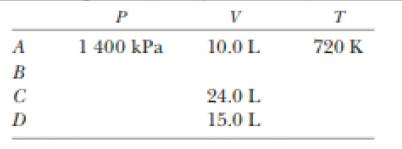
(b) Find the energy added by heat, the work done by the engine, and the change in internal energy for each of the steps A → B, B → C, C → D, and D → A (c) Calculate the efficiency Wnet/|Qk|. (d) Show that the efficiency is equal to 1 - TC/TA, the Carnot efficiency.
(a)
The unknown pressures, volumes and the temperature in the table.
Answer to Problem 22.32P
The values of unknown pressures, volumes and the temperature in the table are,
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Explanation of Solution
Given: The number of moles of a mono atomic ideal gas is
Write the equation of adiabatic process
Here,
The value of
Substitute
Thus, the pressure of the gas at point
Write the ideal gas equation.
Here,
The value of gas constant is
Substitute
Thus, the temperature of the gas at point
In isothermal process, the temperature is constant.
For isothermal process
The temperature of the gas at point
Thus, the temperature of the gas at point
Write the ideal gas equation.
Here,
Substitute
Thus, the pressure of the gas at point
Write the equation of adiabatic process
Here,
Substitute
Thus, the volume of the gas at point
In isothermal process, the temperature is constant.
For isothermal process
The temperature of the gas at point
Thus, the temperature of the gas at point
Write the ideal gas equation.
Here,
Substitute
Thus, the pressure of the gas at point
Form a table and show the unknown value of pressures, volumes and temperatures.
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Conclusion:
Therefore, the values of unknown pressures, volumes and the temperature in the table are,
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b)
The energy added by heat, work done by the engine and the change in internal energy for each of the steps
Answer to Problem 22.32P
The values of energy added by heat, work done by the engine and the change in internal energy for each of the steps in the table are,
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Explanation of Solution
Given: The number of moles of a mono atomic ideal gas is
The process
Write the equation of change in temperature for process
Here,
Substitute
Thus, the change in internal energy for process
Write the equation of work done by the engine for process
Substitute
Thus, the work done by the engine for process
Write the equation of isothermal process
Substitute
Thus, the energy added by heat for process
Write the equation of change in temperature for process
Here,
The value of
Substitute
Substitute
Thus, the change in internal energy for process
The process
Thus, the energy added by heat for process
Write the equation of change in internal energy for process
Substitute
Thus, the work done by the engine for process
The process
Write the equation of change in temperature for process
Substitute
Thus, the change in internal energy for process
Write the equation of work done by the engine for process
Substitute
Thus, the work done by the engine for process
Write the equation of isothermal process
Substitute
Thus, the energy added by heat for process
Write the equation of change in temperature for process
Substitute
Substitute
Thus, the change in internal energy for process
The process
Thus, the energy added by heat for process
Write the equation of change in internal energy for process
Substitute
Thus, the work done by the engine for process
Form a table and show the value of energy added by heat, work done by the engine and the change in internal energy.
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Conclusion:
Therefore, the values of energy added by heat, work done by the engine and the change in internal energy for each of the steps in the table are,
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(c)
The value of efficiency
Answer to Problem 22.32P
The value of efficiency
Explanation of Solution
Given: The number of moles of a mono atomic ideal gas is
Calculate the net work done from the table is,
Write the equation for efficiency.
Here,
Substitute
The value of efficiency
Conclusion:
Therefore, the value of efficiency
(d)
To show: The efficiency is equal to the Carnot efficiency
Answer to Problem 22.32P
The efficiency is equal to the Carnot efficiency
Explanation of Solution
Given: The number of moles of a mono atomic ideal gas is
Write the equation for Carnot efficiency.
Here,
The value of
Substitute
Thus, the Carnot efficiency is
Write the equation for efficiency.
Substitute
The value of efficiency is
Conclusion:
Therefore, the efficiency is equal to the Carnot efficiency
Want to see more full solutions like this?
Chapter 22 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- Of the following, which is not a statement of the second law of thermodynamics? (a) No heat engine operating in a cycle can absorb energy from a reservoir and use it entirely to do work, (b) No real engine operating between two energy reservoirs can be more efficient than a Carnot engine operating between the same two reservoirs, (c) When a system undergoes a change in state, the change in the internal energy of the system is the sum of the energy transferred to the system by heat and the work done on the system, (d) The entropy of the Universe increases in all natural processes, (e) Energy will not spontaneously transfer by heat from a cold object to a hot object.arrow_forwardThe compression ratio of an Otto cycle as shown in Figure 21.12 is VA/VB = 8.00. At the beginning A of the compression process, 500 cm3 of gas is at 100 kPa and 20.0C. At the beginning of the adiabatic expansion, the temperature is TC = 750C. Model the working fluid as an ideal gas with = 1.40. (a) Fill in this table to follow the states of the gas: (b) Fill in this table to follow the processes: (c) Identify the energy input |Qh|, (d) the energy exhaust |Qc|, and (e) the net output work Weng. (f) Calculate the efficiency. (g) Find the number of crankshaft revolutions per minute required for a one-cylinder engine to have an output power of 1.00 kW = 1.34 hp. Note: The thermodynamic cycle involves four piston strokes.arrow_forwardA Carnot engine employs 1.5 mol of nitrogen gas as a working substance, which is considered as an ideal diatomic gas with =7.5 at the working temperatures of the engine. The Carnot cycle goes in the cycle ABCDA with AB being an isothermal expansion. The volume at points A and C of the cycle are 5.0103 m3 and 0.15 L, respectively. The engine operates between two thermal baths of temperature 500 K 300 K. (a) Find the values of volume at B and D. (b) How much heat is absorbed by the gas in the AB isothermal expansion? (c) How much work is done by the gas in the AB isothermal expansion? (d) How much heat is given up by the gas in the CD isothermal expansion? (e) How much work is done by the gas in the CD isothermal compression? (f) How much work is done by the gas in the BC adiabatic expansion? (g) How much work is done by the gas in the DA adiabatic compression? (h) Find the value of efficiency of the engine based on the net and heat input. Compare this value to the efficiency of a Carnot engine based on the temperatures of the baths.arrow_forward
- A 2.00-mol sample of a diatomic ideal gas expands slowly and adiabatically from a pressure of 5.00 atm and a volume of 12.0 L to a final volume of 30.0 L. (a) What is the final pressure of the gas? (b) What are the initial and final temperatures? Find (c) Q, (d) Eint, and (e) W for the gas during this process.arrow_forwardThe arrow OA in the PV diagram shown in Figure OQ22.11 represents a reversible adiabatic expansion of an ideal gas. The same sample of gas, starting from the same state O. now undergoes an adiabatic free expansion to the same final volume. What point on the diagram could represent the final state of the gas? (a) the same point A as for the reversible expansion (b) point B (c) point C (d) any of those choices (e) none of those choicesarrow_forwardOne mole of an ideal gas does 3 000 J of work on its surroundings as it expands isothermally to a final pressure of 1.00 atm and volume of 25.0 L. Determine (a) the initial volume and (b) the temperature of the gas.arrow_forward
- Which of the following is true for the entropy change of a system that undergoes a reversible, adiabatic process? (a) S 0 (b) S = 0 (c) S 0arrow_forwardFigure P21.45 shows a cyclic process ABCDA for 1.00 mol of an ideal gas. The gas is initially at Pi = 1.50 105 Pa, Vi = 1.00 103 m3 (point A in Fig. P21.45). a. What is the net work done on the gas during the cycle? b. What is the net amount of energy added by heat to this gas during the cycle? FIGURE P21.45arrow_forwardTrue or False: The entropy change in an adiabatic process must be zero because Q = 0.arrow_forward
- Find the work done in the quasi-static processes shown below. The states are given as (p, V) values for the points in the PV plane: 1 (3 atm, 4 L), 2 (3 atm, 6 L), 3 (5 atm, 4 L), 4 (2 atm, 6 L), 5 (4 atm, 2 L), 6 (5 atm, 5 L) and 7 (2 atm, 5 L).arrow_forwardA sample of a monatomic ideal gas is contained in a cylinder with a piston. Its state is represented by the dot in the PV diagram shown in Figure OQ18.9. Arrows A through E represent isobaric, isothermal, adiabatic, and isovolumetric processes that the sample can undergo. In each process except D, the volume changes by a factor of 2. All five processes are reversible. Rank the processes according to the change in entropy of the gas from the largest positive value to the largest-magnitude negative value. In your rankings, display any cases of equality. Figure OQ18.9arrow_forwardA copper rod of cross-sectional area 5.0 cm2 and length 5.0 m conducts heat from a heat reservoir at 373 K to one at 273 K. What is the time rate of change of the universe's entropy for this process?arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
 Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





