
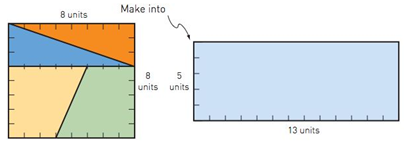
The enlarging area paradox (S). The square shown here has sides equal to 8 (a Fibonacci number) and thus has area equal to
The square can be cut up into four pieces whereby the short sides have lengths 3 and 5, as illustrated. (You will find these pieces in the kit that accompanied your book.) Now use those pieces to construct a rectangle having base 13 and height 5. The area of this rectangle is
So by moving around the four pieces, we increased the area by 1 unit! Using the puzzle pieces from your kit, do the experiment and then explain this impossible feat. Show this puzzle to your friends and record their reactions.
Want to see the full answer?
Check out a sample textbook solution
Chapter 2 Solutions
HEART OF MATHEMATICS
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
Basic Business Statistics, Student Value Edition
Precalculus: Mathematics for Calculus (Standalone Book)
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
Elementary Statistics
University Calculus: Early Transcendentals (4th Edition)
- Show that there is no triangle for which a=4 feet, b=14 feet, and A=60.arrow_forwardWrite three of the properties of triangles from this section and then explain each in your own words.arrow_forwardAn artist wants to make a small monument in the shape of a square base topped by a right triangle, as shown below. The square base will be adjacent to one leg of the triangle. The other leg of the triangle will measure 2 feet and the hypotenuse will be 5 feet. (a) Use the Pythagorean Theorem to find the length of a side of the square base. Round your answer to the nearest tenth of a foot. (b) Find the exact area of the face of the square base.arrow_forward
- A hole is cut in a rectangular metal plate as shown in Figure 4-8. To find the area of a rectangle, multiply the length by the width. Determine the area of the plate after the hole has been removed. All dimensions are in inches. The area will be in square inches.arrow_forwardA landscaper wants to put a square reflecting pool next to a triangular deck, as shown below. The triangular deck is a right triangle, with legs of length 9 feet and 11 feet, and the pool will be adjacent to the hypotenuse. (a) Use the Pythagorean Theorem to find the length of a side of the pool. Round your answer to the nearest tenth of a foot. (b) Find the exact area of the pool.arrow_forwardThe imaginary number i has the property that i2 = ___________________ .arrow_forward
 Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage





