Chapter 2.1, Problem 77E

(a)

To determine

To explain:The reason to restrict the interval $0<\theta <\frac{\pi }{2}$ to show that the right-hand limit of the function is 1.

Explanation of Solution

Given information:The function is $\underset{\theta \to 0}{\lim }\frac{\left(\sin \theta \right)}{\theta }=1$ and the interval is $0<\theta <\frac{\pi }{2}$ .

For the right hand limit of given function check the points close to $\theta =0$ from the right side. All the points to the right side of the 0 are all positive.

The restrict interval to $0<\theta <\frac{\pi }{2}$ is correct to find the right-hand limit because the right hand limit for the given function depends on the positive values of $\theta$ closer to 0.

(b)

To determine

To show:The area of $\Delta OAP$ is $\frac{1}{2}\sin \theta$ , the area of sector OAP is $\frac{\theta }{2}$ and area of $\Delta OAT$ is $\frac{1}{2}\tan \theta$ .

Explanation of Solution

Given information:The figure is given below:

  

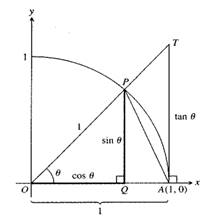
Proof:

The formula for the area of triangle is given by,

  $\text{Area}=\frac{1}{2}\times \text{base}\times \text{height}$

In $\Delta OAP$ , base OA is 1 and height AT is $\tan \theta$ . So,

  $\begin{array}{c}\text{Area of }\Delta OAT=\frac{1}{2}\times \text{1}\times \text{tan}\theta \\ \text{=}\frac{\tan \theta }{2}\end{array}$

In $\Delta OAT$ , base OA is 1 and height is $\sin \theta$ . So,

  $\begin{array}{c}\text{Area of }\Delta OAP=\frac{1}{2}\times \text{1}\times \text{sin}\theta \\ \text{=}\frac{1}{2}\sin \theta \end{array}$

The formula for the area of a sector with radius r is given by,

  $\text{Area of sector}=\frac{\theta }{360°}\times \pi r^2$

The radius of the sector is 1 with central angle $\theta$ . So, the area of sector OAP is:

  $\begin{array}{c}\text{Area of sector }OAP=\frac{\theta }{2\pi }\times \pi {\left(1\right)}^2\\ =\frac{\theta }{2}\end{array}$

Hence, it is proved that area of $\Delta OAP$ is $\frac{1}{2}\sin \theta$ , the area of sector OAP is $\frac{\theta }{2}$ and area of $\Delta OAT$ is $\frac{1}{2}\tan \theta$ .

(c)

To determine

To show:The inequality $\frac{1}{2}\sin \theta <\frac{1}{2}\theta <\frac{1}{2}\tan \theta$ , for the interval $0<\theta <\frac{\pi }{2}$ .

Explanation of Solution

Given information:The figure is given below:

  

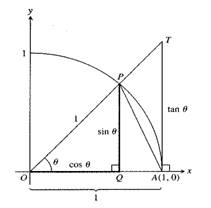
Proof:

From part (b), it is proved that that area of $\Delta OAP$ is $\frac{1}{2}\sin \theta$ , the area of sector OAP is $\frac{\theta }{2}$ and area of $\Delta OAT$ is $\frac{1}{2}\tan \theta$ .

To prove the given inequality, compare the areas of $\Delta OAP$ , $\Delta OAT$ and sector OAP . From the figure it can observed that $\Delta OAP$ is contained in the sector OAP . So,

  $\frac{1}{2}\sin \theta <\frac{1}{2}\theta \mathrm{...}\left(1\right)$

Also, the area of sector OAP contains under the region of $\Delta OAP$ . So,

  $\frac{1}{2}\theta <\frac{1}{2}\tan \theta \mathrm{...}\left(2\right)$

Now, compare inequality (1) and (2).

  $\frac{1}{2}\sin \theta <\frac{1}{2}\theta <\frac{1}{2}\tan \theta$

Hence, theinequality $\frac{1}{2}\sin \theta <\frac{1}{2}\theta <\frac{1}{2}\tan \theta$ is proved, for the interval $0<\theta <\frac{\pi }{2}$ .

(d)

To determine

To show:The inequality $\frac{1}{2}\sin \theta <\frac{1}{2}\theta <\frac{1}{2}\tan \theta$ can be written as $1<\frac{\theta }{\sin \theta }<\frac{1}{\cos \theta }$ for the interval $0<\theta <\frac{\pi }{2}$ .

Explanation of Solution

Proof:

From part (c), for the interval $0<\theta <\frac{\pi }{2}$ the inequality $\frac{1}{2}\sin \theta <\frac{1}{2}\theta <\frac{1}{2}\tan \theta$ is proved.

Multiply the inequality by 2.

  $\begin{array}{c}2\times \frac{1}{2}\sin \theta <2\times \frac{1}{2}\theta <\frac{1}{2}2\times \tan \theta \\ \sin \theta <\theta <\tan \theta \end{array}$

Divide the inequality by $\sin \theta$ .

  $\begin{array}{c}\frac{\sin \theta }{\sin \theta }<\frac{\theta }{\sin \theta }<\frac{\tan \theta }{\sin \theta }\\ 1<\frac{\theta }{\sin \theta }<\frac{\sin \theta }{\cos \theta }\times \frac{1}{\sin \theta }\\ 1<\frac{\theta }{\sin \theta }<\frac{1}{\cos \theta }\end{array}$

Hence, theinequality proved in part (c) can be written as $1<\frac{\theta }{\sin \theta }<\frac{1}{\cos \theta }$ , for the interval $0<\theta <\frac{\pi }{2}$ .

(e)

To determine

To show:The inequality $1<\frac{\theta }{\sin \theta }<\frac{1}{\cos \theta }$ can be written as $\cos \theta <\frac{\sin \theta }{\theta }<1$ for the interval $0<\theta <\frac{\pi }{2}$ .

Explanation of Solution

Proof:

From part (d), for the interval $0<\theta <\frac{\pi }{2}$ the inequality $1<\frac{\theta }{\sin \theta }<\frac{1}{\cos \theta }$ is proved.

Use the inverse property of inequality and take the inverse of each term to rewrite the inequality.

  $\begin{array}{c}1>\frac{\sin \theta }{\theta }>\cos \theta \\ \cos \theta <\frac{\sin \theta }{\theta }<1\end{array}$

Hence, theinequality proved in part (d) can be written as $\cos \theta <\frac{\sin \theta }{\theta }<1$ for the interval $0<\theta <\frac{\pi }{2}$ .

(f)

To determine

To show:The result $\underset{\theta \to 0^{+}}{\lim }\frac{\sin \theta }{\theta }=1$ by Sandwich theorem.

Explanation of Solution

Proof:

Sandwich theorem: If a function $f\left(x\right)$ lies between two functions such that $g\left(x\right)\le f\left(x\right)\le h\left(x\right)$ for $x=c$ and both functions have the same limit L , then

  $\underset{x\to c}{\lim }f\left(x\right)=L$

From part (e), the condition for Sandwich theorem the inequality can be written as:

  $\cos \theta \le \frac{\sin \theta }{\theta }\le 1$

The limit of the function $\cos \theta$ at $\theta =0^{+}$ is:

  $\begin{array}{c}\underset{\theta \to 0^{+}}{\lim }\cos \theta =\cos 0\\ =1\end{array}$

The limit of the function 1 at $\theta =0^{+}$ is:

  $\underset{\theta \to 0^{+}}{\lim }1=1$

Now, by Sandwich theorem $\underset{\theta \to 0^{+}}{\lim }\frac{\sin \theta }{\theta }=1$ is also true.

Hence, theresult $\underset{\theta \to 0^{+}}{\lim }\frac{\sin \theta }{\theta }=1$ is proved by Sandwich theorem.

(g)

To determine

To show:The function $\frac{\sin \theta }{\theta }$ is an even function.

Explanation of Solution

Given information: The function is $f\left(\theta \right)=\frac{\sin \theta }{\theta }$ .

Proof:

Even function: If $f\left(x\right)=f\left(-x\right)$ , then the function is said to be an even function.

Substitute $-\theta$ for $\theta$ in the given function.

  $\begin{array}{c}f\left(-\theta \right)=\frac{\sin \left(-\theta \right)}{\left(-\theta \right)}\\ =\frac{-\sin \theta }{-\theta }\\ =\frac{\sin \theta }{\theta }\\ =f\left(\theta \right)\end{array}$

Hence, it is proved that $\frac{\sin \theta }{\theta }$ is an even function.

(g)

To determine

To show:The result $\underset{\theta \to 0^{-}}{\lim }\frac{\sin \theta }{\theta }=1$ by using that $\frac{\sin \theta }{\theta }$ is an even function.

Explanation of Solution

Given information: The function is $f\left(\theta \right)=\frac{\sin \theta }{\theta }$ .

Proof:

It is known that if a function is even function, then its graph is symmetric about the y -axis.

In part (f), it is already proved that the right-hand limit of the function at 0 is 1. From part (g), it is proved that that $\frac{\sin \theta }{\theta }$ is an even function. So, left hand limit is equal to the right hand limit.

The left hand limit is:

  $\underset{\theta \to 0^{-}}{\lim }\frac{\sin \theta }{\theta }=1$

Hence, the result $\underset{\theta \to 0^{-}}{\lim }\frac{\sin \theta }{\theta }=1$ is proved.

(h)

To determine

To show:The result $\underset{\theta \to 0}{\lim }\frac{\sin \theta }{\theta }=1$ .

Explanation of Solution

Given information: The function is $f\left(\theta \right)=\frac{\sin \theta }{\theta }$ .

Proof:

If the left hand limit and right hand limit of a function is equal, then the limit at that point is the same as RHL or LHL.

In above parts it is already proved that at $\theta =0$ , the right hand limit $\underset{\theta \to 0^{+}}{\lim }\frac{\sin \theta }{\theta }=1$ is equal to the left hand limit $\underset{\theta \to 0^{-}}{\lim }\frac{\sin \theta }{\theta }=1$ . So,

  $\underset{\theta \to 0}{\lim }\frac{\sin \theta }{\theta }=1$

Hence, the result $\underset{\theta \to 0}{\lim }\frac{\sin \theta }{\theta }=1$ is proved.