AP CALCULUS TEST PREP-WORKBOOK
6th Edition
ISBN: 9781418300258
Author: Demana
Publisher: SAVVAS L
expand_more
expand_more
format_list_bulleted
Question
Chapter 2.1, Problem 30E
(a.)
To determine
To sketch: a graph of elevation
(a.)
Expert Solution
Answer to Problem 30E
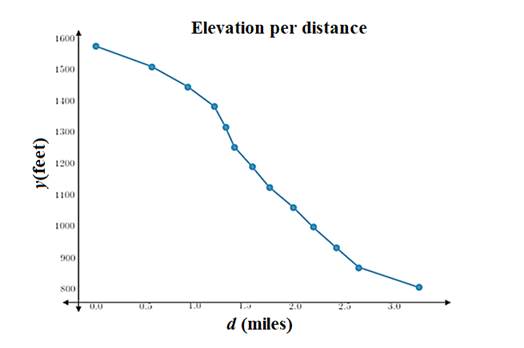
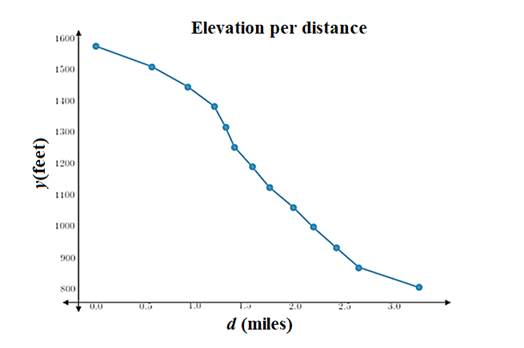
The required graph is shown.
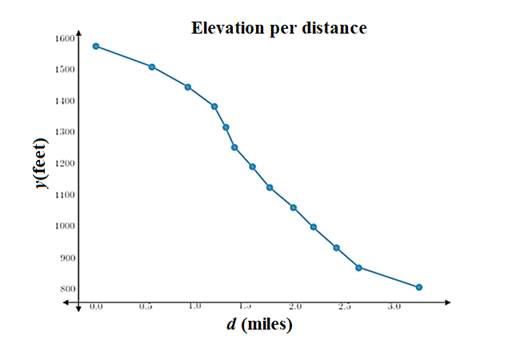
Explanation of Solution
Given:
| Elevation Along Bear Creek | |
| Distance Downriver | River Elevation |
| 0.00 | 1577 |
| 0.56 | 1512 |
| 0.92 | 1448 |
| 1.19 | 1384 |
| 1.30 | 1319 |
| 1.39 | 1255 |
| 1.57 | 1191 |
| 1.74 | 1126 |
| 1.98 | 1062 |
| 2.18 | 998 |
| 2.41 | 933 |
| 2.64 | 869 |
| 3.24 | 805 |
Calculation:
Plot the points on graph and join them
(b.)
To determine
To obtain: an approximate graph of the derivative.
(b.)
Expert Solution
Answer to Problem 30E
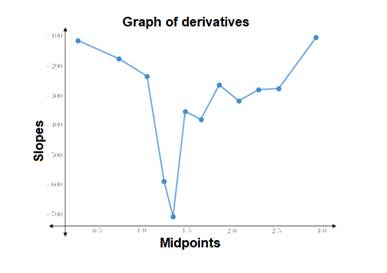
The graph of the derivative is shown.
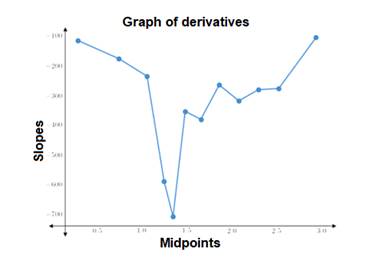
Explanation of Solution
Given:
| Elevation Along Bear Creek | |
| Distance Downriver | River Elevation |
| 0.00 | 1577 |
| 0.56 | 1512 |
| 0.92 | 1448 |
| 1.19 | 1384 |
| 1.30 | 1319 |
| 1.39 | 1255 |
| 1.57 | 1191 |
| 1.74 | 1126 |
| 1.98 | 1062 |
| 2.18 | 998 |
| 2.41 | 933 |
| 2.64 | 869 |
| 3.24 | 805 |
Concept used:
The derivative of a function is represented by slope of graph.
Calculation:
Create a table with mid point of each interval and their respective slopes.
| Elevation Along Bear Creek | |
| Distance Downriver | River Elevation |
Now plot the above points on the graph and join them.
(c.)
To determine
The units of measure would be appropriate for a gradient in this problem.
(c.)
Expert Solution
Answer to Problem 30E
The unit of gradient is feet per mile.
Explanation of Solution
Given:
| Elevation Along Bear Creek | |
| Distance Downriver (miles) | River Elevation (feet) |
| 0.00 | 1577 |
| 0.56 | 1512 |
| 0.92 | 1448 |
| 1.19 | 1384 |
| 1.30 | 1319 |
| 1.39 | 1255 |
| 1.57 | 1191 |
| 1.74 | 1126 |
| 1.98 | 1062 |
| 2.18 | 998 |
| 2.41 | 933 |
| 2.64 | 869 |
| 3.24 | 805 |
Concept used:
The average change in elevation over a given distance is called a gradient.
Conclusion:
Here, the elevation is given in feet and the distance down the river is given in miles.
Thus, the units of the gradient will be feet per mile.
(d.)
To determine
The units of measure would be appropriate for derivative.
(d.)
Expert Solution
Answer to Problem 30E
The units of the gradient will be feet per mile.
Explanation of Solution
Given:
| Elevation Along Bear Creek | |
| Distance Downriver (miles) | River Elevation (feet) |
| 0.00 | 1577 |
| 0.56 | 1512 |
| 0.92 | 1448 |
| 1.19 | 1384 |
| 1.30 | 1319 |
| 1.39 | 1255 |
| 1.57 | 1191 |
| 1.74 | 1126 |
| 1.98 | 1062 |
| 2.18 | 998 |
| 2.41 | 933 |
| 2.64 | 869 |
| 3.24 | 805 |
Concept used:
Derivative is given by the slope.
Here, the average change in elevation over a given distance is slope.
Conclusion:
Here, the elevation is given in feet and the distance down the river is given in miles.
Thus, the units of the gradient will be feet per mile.
(e)
To determine
To identify: The most dangerous section of the river by analyzing the graph in (a).
(e)
Expert Solution
Answer to Problem 30E
The most dangerous section of the river is from 1.2 to 1.5 miles.
Explanation of Solution
Given:
| Elevation Along Bear Creek | |
| Distance Downriver (miles) | River Elevation (feet) |
| 0.00 | 1577 |
| 0.56 | 1512 |
| 0.92 | 1448 |
| 1.19 | 1384 |
| 1.30 | 1319 |
| 1.39 | 1255 |
| 1.57 | 1191 |
| 1.74 | 1126 |
| 1.98 | 1062 |
| 2.18 | 998 |
| 2.41 | 933 |
| 2.64 | 869 |
| 3.24 | 805 |
Conclusion:
In the graph, the steepest part which is from 1.2 to 1.5 miles.
Chapter 2 Solutions
AP CALCULUS TEST PREP-WORKBOOK
Ch. 2.1 - Prob. 1QRCh. 2.1 - Prob. 2QRCh. 2.1 - Prob. 3QRCh. 2.1 - Prob. 4QRCh. 2.1 - Prob. 5QRCh. 2.1 - Prob. 6QRCh. 2.1 - Prob. 7QRCh. 2.1 - Prob. 8QRCh. 2.1 - Prob. 9QRCh. 2.1 - Prob. 10QR
Ch. 2.1 - Prob. 1ECh. 2.1 - Prob. 2ECh. 2.1 - Prob. 3ECh. 2.1 - Prob. 4ECh. 2.1 - Prob. 5ECh. 2.1 - Prob. 6ECh. 2.1 - Prob. 7ECh. 2.1 - Prob. 8ECh. 2.1 - Prob. 9ECh. 2.1 - Prob. 10ECh. 2.1 - Prob. 11ECh. 2.1 - Prob. 12ECh. 2.1 - Prob. 13ECh. 2.1 - Prob. 14ECh. 2.1 - Prob. 15ECh. 2.1 - Prob. 16ECh. 2.1 - Prob. 17ECh. 2.1 - Prob. 18ECh. 2.1 - Prob. 19ECh. 2.1 - Prob. 20ECh. 2.1 - Prob. 21ECh. 2.1 - Prob. 22ECh. 2.1 - Prob. 23ECh. 2.1 - Prob. 24ECh. 2.1 - Prob. 25ECh. 2.1 - Prob. 26ECh. 2.1 - Prob. 27ECh. 2.1 - Prob. 28ECh. 2.1 - Prob. 29ECh. 2.1 - Prob. 30ECh. 2.1 - Prob. 31ECh. 2.1 - Prob. 32ECh. 2.1 - Prob. 33ECh. 2.1 - Prob. 34ECh. 2.1 - Prob. 35ECh. 2.1 - Prob. 36ECh. 2.1 - Prob. 37ECh. 2.1 - Prob. 38ECh. 2.1 - Prob. 39ECh. 2.1 - Prob. 40ECh. 2.1 - Prob. 41ECh. 2.1 - Prob. 42ECh. 2.1 - Prob. 43ECh. 2.1 - Prob. 44ECh. 2.1 - Prob. 45ECh. 2.1 - Prob. 46ECh. 2.2 - Prob. 1QRCh. 2.2 - Prob. 2QRCh. 2.2 - Prob. 3QRCh. 2.2 - Prob. 4QRCh. 2.2 - Prob. 5QRCh. 2.2 - Prob. 6QRCh. 2.2 - Prob. 7QRCh. 2.2 - Prob. 8QRCh. 2.2 - Prob. 9QRCh. 2.2 - Prob. 10QRCh. 2.2 - Prob. 1ECh. 2.2 - Prob. 2ECh. 2.2 - Prob. 3ECh. 2.2 - Prob. 4ECh. 2.2 - Prob. 5ECh. 2.2 - Prob. 6ECh. 2.2 - Prob. 7ECh. 2.2 - Prob. 8ECh. 2.2 - Prob. 9ECh. 2.2 - Prob. 10ECh. 2.2 - Prob. 11ECh. 2.2 - Prob. 12ECh. 2.2 - Prob. 13ECh. 2.2 - Prob. 14ECh. 2.2 - Prob. 15ECh. 2.2 - Prob. 16ECh. 2.2 - Prob. 17ECh. 2.2 - Prob. 18ECh. 2.2 - Prob. 19ECh. 2.2 - Prob. 20ECh. 2.2 - Prob. 21ECh. 2.2 - Prob. 22ECh. 2.2 - Prob. 23ECh. 2.2 - Prob. 24ECh. 2.2 - Prob. 25ECh. 2.2 - Prob. 26ECh. 2.2 - Prob. 27ECh. 2.2 - Prob. 28ECh. 2.2 - Prob. 29ECh. 2.2 - Prob. 30ECh. 2.2 - Prob. 31ECh. 2.2 - Prob. 32ECh. 2.2 - Prob. 33ECh. 2.2 - Prob. 34ECh. 2.2 - Prob. 35ECh. 2.2 - Prob. 36ECh. 2.2 - Prob. 37ECh. 2.2 - Prob. 38ECh. 2.2 - Prob. 39ECh. 2.2 - Prob. 40ECh. 2.2 - Prob. 41ECh. 2.2 - Prob. 42ECh. 2.2 - Prob. 43ECh. 2.2 - Prob. 44ECh. 2.2 - Prob. 45ECh. 2.2 - Prob. 46ECh. 2.2 - Prob. 47ECh. 2.2 - Prob. 48ECh. 2.3 - Prob. 1QRCh. 2.3 - Prob. 2QRCh. 2.3 - Prob. 3QRCh. 2.3 - Prob. 4QRCh. 2.3 - Prob. 5QRCh. 2.3 - Prob. 6QRCh. 2.3 - Prob. 7QRCh. 2.3 - Prob. 8QRCh. 2.3 - Prob. 9QRCh. 2.3 - Prob. 10QRCh. 2.3 - Prob. 1ECh. 2.3 - Prob. 2ECh. 2.3 - Prob. 3ECh. 2.3 - Prob. 4ECh. 2.3 - Prob. 5ECh. 2.3 - Prob. 6ECh. 2.3 - Prob. 7ECh. 2.3 - Prob. 8ECh. 2.3 - Prob. 9ECh. 2.3 - Prob. 10ECh. 2.3 - Prob. 11ECh. 2.3 - Prob. 12ECh. 2.3 - Prob. 13ECh. 2.3 - Prob. 14ECh. 2.3 - Prob. 15ECh. 2.3 - Prob. 16ECh. 2.3 - Prob. 17ECh. 2.3 - Prob. 18ECh. 2.3 - Prob. 19ECh. 2.3 - Prob. 20ECh. 2.3 - Prob. 21ECh. 2.3 - Prob. 22ECh. 2.3 - Prob. 23ECh. 2.3 - Prob. 24ECh. 2.3 - Prob. 25ECh. 2.3 - Prob. 26ECh. 2.3 - Prob. 27ECh. 2.3 - Prob. 28ECh. 2.3 - Prob. 29ECh. 2.3 - Prob. 30ECh. 2.3 - Prob. 31ECh. 2.3 - Prob. 32ECh. 2.3 - Prob. 33ECh. 2.3 - Prob. 34ECh. 2.3 - Prob. 35ECh. 2.3 - Prob. 36ECh. 2.3 - Prob. 37ECh. 2.3 - Prob. 38ECh. 2.3 - Prob. 39ECh. 2.3 - Prob. 40ECh. 2.3 - Prob. 41ECh. 2.3 - Prob. 42ECh. 2.3 - Prob. 43ECh. 2.3 - Prob. 44ECh. 2.3 - Prob. 45ECh. 2.3 - Prob. 46ECh. 2.3 - Prob. 47ECh. 2.3 - Prob. 48ECh. 2.3 - Prob. 49ECh. 2.3 - Prob. 50ECh. 2.3 - Prob. 51ECh. 2.3 - Prob. 52ECh. 2.3 - Prob. 53ECh. 2.3 - Prob. 54ECh. 2.3 - Prob. 55ECh. 2.3 - Prob. 56ECh. 2.3 - Prob. 57ECh. 2.3 - Prob. 58ECh. 2.3 - Prob. 59ECh. 2.3 - Prob. 1QQCh. 2.3 - Prob. 2QQCh. 2.3 - Prob. 3QQCh. 2.3 - Prob. 4QQCh. 2.4 - Prob. 1QRCh. 2.4 - Prob. 2QRCh. 2.4 - Prob. 3QRCh. 2.4 - Prob. 4QRCh. 2.4 - Prob. 5QRCh. 2.4 - Prob. 6QRCh. 2.4 - Prob. 7QRCh. 2.4 - Prob. 8QRCh. 2.4 - Prob. 9QRCh. 2.4 - Prob. 10QRCh. 2.4 - Prob. 1ECh. 2.4 - Prob. 2ECh. 2.4 - Prob. 3ECh. 2.4 - Prob. 4ECh. 2.4 - Prob. 5ECh. 2.4 - Prob. 6ECh. 2.4 - Prob. 7ECh. 2.4 - Prob. 8ECh. 2.4 - Prob. 9ECh. 2.4 - Prob. 10ECh. 2.4 - Prob. 11ECh. 2.4 - Prob. 12ECh. 2.4 - Prob. 13ECh. 2.4 - Prob. 14ECh. 2.4 - Prob. 15ECh. 2.4 - Prob. 16ECh. 2.4 - Prob. 17ECh. 2.4 - Prob. 18ECh. 2.4 - Prob. 19ECh. 2.4 - Prob. 20ECh. 2.4 - Prob. 21ECh. 2.4 - Prob. 22ECh. 2.4 - Prob. 23ECh. 2.4 - Prob. 24ECh. 2.4 - Prob. 25ECh. 2.4 - Prob. 26ECh. 2.4 - Prob. 27ECh. 2.4 - Prob. 28ECh. 2.4 - Prob. 29ECh. 2.4 - Prob. 30ECh. 2.4 - Prob. 31ECh. 2.4 - Prob. 32ECh. 2.4 - Prob. 33ECh. 2.4 - Prob. 34ECh. 2.4 - Prob. 35ECh. 2.4 - Prob. 36ECh. 2.4 - Prob. 37ECh. 2.4 - Prob. 38ECh. 2.4 - Prob. 39ECh. 2.4 - Prob. 40ECh. 2.4 - Prob. 41ECh. 2.4 - Prob. 42ECh. 2.4 - Prob. 43ECh. 2.4 - Prob. 44ECh. 2.4 - Prob. 45ECh. 2.4 - Prob. 46ECh. 2.4 - Prob. 47ECh. 2.4 - Prob. 48ECh. 2.4 - Prob. 49ECh. 2.4 - Prob. 50ECh. 2.5 - Prob. 1QRCh. 2.5 - Prob. 2QRCh. 2.5 - Prob. 3QRCh. 2.5 - Prob. 4QRCh. 2.5 - Prob. 5QRCh. 2.5 - Prob. 6QRCh. 2.5 - Prob. 7QRCh. 2.5 - Prob. 8QRCh. 2.5 - Prob. 9QRCh. 2.5 - Prob. 10QRCh. 2.5 - Prob. 1ECh. 2.5 - Prob. 2ECh. 2.5 - Prob. 3ECh. 2.5 - Prob. 4ECh. 2.5 - Prob. 5ECh. 2.5 - Prob. 6ECh. 2.5 - Prob. 7ECh. 2.5 - Prob. 8ECh. 2.5 - Prob. 9ECh. 2.5 - Prob. 10ECh. 2.5 - Prob. 11ECh. 2.5 - Prob. 12ECh. 2.5 - Prob. 13ECh. 2.5 - Prob. 14ECh. 2.5 - Prob. 15ECh. 2.5 - Prob. 16ECh. 2.5 - Prob. 17ECh. 2.5 - Prob. 18ECh. 2.5 - Prob. 19ECh. 2.5 - Prob. 20ECh. 2.5 - Prob. 21ECh. 2.5 - Prob. 22ECh. 2.5 - Prob. 23ECh. 2.5 - Prob. 24ECh. 2.5 - Prob. 25ECh. 2.5 - Prob. 26ECh. 2.5 - Prob. 27ECh. 2.5 - Prob. 28ECh. 2.5 - Prob. 29ECh. 2.5 - Prob. 30ECh. 2.5 - Prob. 31ECh. 2.5 - Prob. 32ECh. 2.5 - Prob. 33ECh. 2.5 - Prob. 34ECh. 2.5 - Prob. 35ECh. 2.5 - Prob. 36ECh. 2.5 - Prob. 37ECh. 2.5 - Prob. 38ECh. 2.5 - Prob. 39ECh. 2.5 - Prob. 40ECh. 2.5 - Prob. 41ECh. 2.5 - Prob. 42ECh. 2.5 - Prob. 43ECh. 2.5 - Prob. 44ECh. 2.5 - Prob. 45ECh. 2.5 - Prob. 46ECh. 2.5 - Prob. 47ECh. 2.5 - Prob. 48ECh. 2.5 - Prob. 49ECh. 2.5 - Prob. 50ECh. 2.5 - Prob. 51ECh. 2.5 - Prob. 52ECh. 2.5 - Prob. 1QQCh. 2.5 - Prob. 2QQCh. 2.5 - Prob. 3QQCh. 2.5 - Prob. 4QQCh. 2 - Prob. 1RWDTCh. 2 - Prob. 2RWDTCh. 2 - Prob. 3RWDTCh. 2 - Prob. 4RWDTCh. 2 - Prob. 5RWDTCh. 2 - Prob. 6RWDTCh. 2 - Prob. 7RWDTCh. 2 - Prob. 8RWDTCh. 2 - Prob. 9RWDTCh. 2 - Prob. 10RWDTCh. 2 - Prob. 1RECh. 2 - Prob. 2RECh. 2 - Prob. 3RECh. 2 - Prob. 4RECh. 2 - Prob. 5RECh. 2 - Prob. 6RECh. 2 - Prob. 7RECh. 2 - Prob. 8RECh. 2 - Prob. 9RECh. 2 - Prob. 10RECh. 2 - Prob. 11RECh. 2 - Prob. 12RECh. 2 - Prob. 13RECh. 2 - Prob. 14RECh. 2 - Prob. 15RECh. 2 - Prob. 16RECh. 2 - Prob. 17RECh. 2 - Prob. 18RECh. 2 - Prob. 19RECh. 2 - Prob. 20RECh. 2 - Prob. 21RECh. 2 - Prob. 22RECh. 2 - Prob. 23RECh. 2 - Prob. 24RECh. 2 - Prob. 25RECh. 2 - Prob. 26RECh. 2 - Prob. 27RECh. 2 - Prob. 28RECh. 2 - Prob. 29RECh. 2 - Prob. 30RECh. 2 - Prob. 31RECh. 2 - Prob. 32RECh. 2 - Prob. 33RECh. 2 - Prob. 34RECh. 2 - Prob. 35RECh. 2 - Prob. 36RECh. 2 - Prob. 37RECh. 2 - Prob. 38RECh. 2 - Prob. 39RECh. 2 - Prob. 40RECh. 2 - Prob. 41RECh. 2 - Prob. 42RECh. 2 - Prob. 43RECh. 2 - Prob. 44RECh. 2 - Prob. 45RECh. 2 - Prob. 46RECh. 2 - Prob. 47RECh. 2 - Prob. 48RECh. 2 - Prob. 49RECh. 2 - Prob. 50RECh. 2 - Prob. 51RECh. 2 - Prob. 52RECh. 2 - Prob. 53RECh. 2 - Prob. 54RECh. 2 - Prob. 55RECh. 2 - Prob. 56RECh. 2 - Prob. 57RECh. 2 - Prob. 58RECh. 2 - Prob. 59RECh. 2 - Prob. 60RECh. 2 - Prob. 61RECh. 2 - Prob. 62RECh. 2 - Prob. 63RECh. 2 - Prob. 64RECh. 2 - Prob. 65RECh. 2 - Prob. 66RECh. 2 - Prob. 67RECh. 2 - Prob. 68RECh. 2 - Prob. 69RECh. 2 - Prob. 70RECh. 2 - Prob. 71RECh. 2 - Prob. 72RECh. 2 - Prob. 73RECh. 2 - Prob. 74RECh. 2 - Prob. 75RECh. 2 - Prob. 76RECh. 2 - Prob. 77RECh. 2 - Prob. 78RECh. 2 - Prob. 79RECh. 2 - Prob. 80RECh. 2 - Prob. 81EPCh. 2 - Prob. 82EPCh. 2 - Prob. 83EP
Knowledge Booster
Similar questions
- The graph of f(x) is given below. Select each true statement about the continuity of f(x) at x = 1. Select all that apply: ☐ f(x) is not continuous at x = 1 because it is not defined at x = 1. ☐ f(x) is not continuous at x = 1 because lim f(x) does not exist. x+1 ☐ f(x) is not continuous at x = 1 because lim f(x) ‡ f(1). x+→1 ☐ f(x) is continuous at x = 1.arrow_forwarda is done please show barrow_forwardA homeware company has been approached to manufacture a cake tin in the shape of a "ghost" from the Pac-Man video game to celebrate the 45th Anniversary of the games launch. The base of the cake tin has a characteristic dimension / and is illustrated in Figure 1 below, you should assume the top and bottom of the shape can be represented by semi-circles. The vertical sides of the cake tin have a height of h. As the company's resident mathematician, you need to find the values of r and h that minimise the internal surface area of the cake tin given that the volume of the tin is Vfixed- 2r Figure 1 - Plan view of the "ghost" cake tin base. (a) Show that the Volume (V) of the cake tin as a function of r and his 2(+1)²h V = 2arrow_forward
- 15. Please solve this and show each and every step please. PLEASE no chatgpt can I have a real person solve it please!! I am stuck. I am doing pratice problems and I do not even know where to start with this. The question is Please compute the indicated functional value.arrow_forwardUse a graph of f to estimate lim f(x) or to show that the limit does not exist. Evaluate f(x) near x = a to support your conjecture. Complete parts (a) and (b). x-a f(x)= 1 - cos (4x-4) 3(x-1)² ; a = 1 a. Use a graphing utility to graph f. Select the correct graph below.. A. W → ✓ Each graph is displayed in a [- 1,3] by [0,5] window. B. in ✓ ○ C. und ☑ Use the graphing utility to estimate lim f(x). Select the correct choice below and, if necessary, fill in the answer box to complete your choice. x-1 ○ A. The limit appears to be approximately ☐ . (Round to the nearest tenth as needed.) B. The limit does not exist. b. Evaluate f(x) for values of x near 1 to support your conjecture. X 0.9 0.99 0.999 1.001 1.01 1.1 f(x) ○ D. + ☑ (Round to six decimal places as needed.) Does the table from the previous step support your conjecture? A. No, it does not. The function f(x) approaches a different value in the table of values than in the graph, after the approached values are rounded to the…arrow_forwardx²-19x+90 Let f(x) = . Complete parts (a) through (c) below. x-a a. For what values of a, if any, does lim f(x) equal a finite number? Select the correct choice below and, if necessary, fill in the answer box to complete your choice. x→a+ ○ A. a= (Type an integer or a simplified fraction. Use a comma to separate answers as needed.) B. There are no values of a for which the limit equals a finite number. b. For what values of a, if any, does lim f(x) = ∞o? Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. x→a+ A. (Type integers or simplified fractions) C. There are no values of a that satisfy lim f(x) = ∞. + x-a c. For what values of a, if any, does lim f(x) = -∞0? Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. x→a+ A. Either a (Type integers or simplified fractions) B.arrow_forwardSketch a possible graph of a function f, together with vertical asymptotes, that satisfies all of the following conditions. f(2)=0 f(4) is undefined lim f(x)=1 X-6 lim f(x) = -∞ x-0+ lim f(x) = ∞ lim f(x) = ∞ x-4 _8arrow_forwardDetermine the following limit. lim 35w² +8w+4 w→∞ √49w+w³ 3 Select the correct choice below, and, if necessary, fill in the answer box to complete your choice. ○ A. lim W→∞ 35w² +8w+4 49w+w3 (Simplify your answer.) B. The limit does not exist and is neither ∞ nor - ∞.arrow_forwardCalculate the limit lim X-a x-a 5 using the following factorization formula where n is a positive integer and x-➡a a is a real number. x-a = (x-a) (x1+x-2a+x lim x-a X - a x-a 5 = n- + xa an-2 + an−1)arrow_forwardThe function s(t) represents the position of an object at time t moving along a line. Suppose s(1) = 116 and s(5)=228. Find the average velocity of the object over the interval of time [1,5]. The average velocity over the interval [1,5] is Vav = (Simplify your answer.)arrow_forwardFor the position function s(t) = - 16t² + 105t, complete the following table with the appropriate average velocities. Then make a conjecture about the value of the instantaneous velocity at t = 1. Time Interval Average Velocity [1,2] Complete the following table. Time Interval Average Velocity [1, 1.5] [1, 1.1] [1, 1.01] [1, 1.001] [1,2] [1, 1.5] [1, 1.1] [1, 1.01] [1, 1.001] ப (Type exact answers. Type integers or decimals.) The value of the instantaneous velocity at t = 1 is (Round to the nearest integer as needed.)arrow_forwardFind the following limit or state that it does not exist. Assume b is a fixed real number. (x-b) 40 - 3x + 3b lim x-b x-b ... Select the correct choice below and, if necessary, fill in the answer box to complete your choice. (x-b) 40 -3x+3b A. lim x-b x-b B. The limit does not exist. (Type an exact answer.)arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_iosRecommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage LearningThomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSONCalculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSONCalculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. FreemanCalculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning