
a
To compute: The payoff and the profit for investments when the call option’s exercise price X=$145 assuming that the stock price on the expiration date is $150.
Introduction:
Options: Options are the instruments used in financial transactions. These are derived based on the value of the underlying assets. Normally, the purpose of an option is to provide the buyer an opportunity to buy or sell the underlying asset depending upon the type of contract they possess. There are two types of options- Call option and put option.
a
Answer to Problem 5PS
The call buyer will incur loss of -$0.18 when the exercise price is $145.
Explanation of Solution
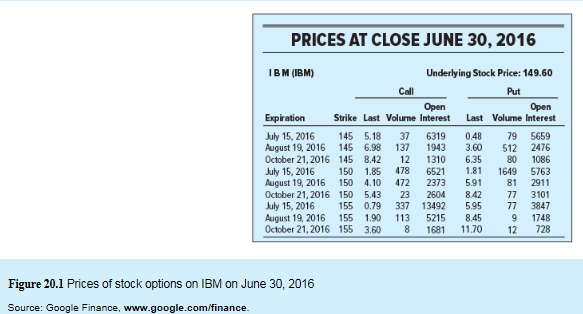
The information given to us is as follows:
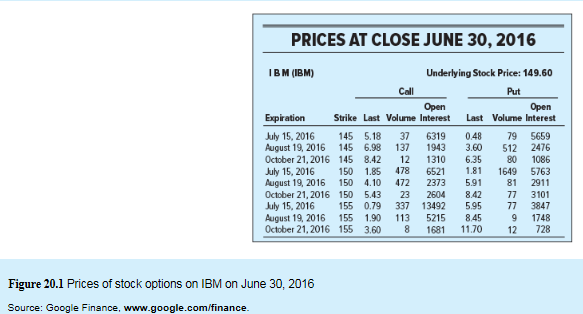
Let us calculate the payoff when Call option X is $145 and stock price on expiry date is $150.
| Calculation of payoff in case of call option | ||
| Position | Stock price > X | Stock price is less than or equal to X |
| Payoff to call holder | Stock price -X | 0 |
| Payoff to call writer | -(Stock price -X) | 0 |
Stock price at expiration is $150.
Exercise or Strike price X=$145.
So, let us now substitute the values in the above table. We get
| Calculation of payoff in case of call option | ||
| Position | Stock price > X | Stock price is less than or equal to X |
| Payoff to call holder | 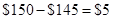 | 0 |
| Payoff to call writer | 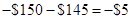 | 0 |
By the above calculation, it is observed that the call writer is prepared to bear the risk in return of option premium as there is loss if stock price increases.
Calculation of profit for investment:
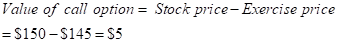
But as per the information given to us, the price of the call option is $5.18 at a strike price $145 on June 2016.
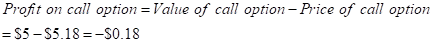
Therefore, the call buyer will incur loss of -$0.18.
b.
To compute: The payoff and the profit for investments when the put option’s exercise price X=$145 assuming that the stock price on the expiration date is $150.
Introduction:
Payoff: In financial terminology, payoff refers to the
b.
Answer to Problem 5PS
The loss incurred by the put buyer will be -$0.48 when the exercise price is $145.
Explanation of Solution
The information given to us is as follows:
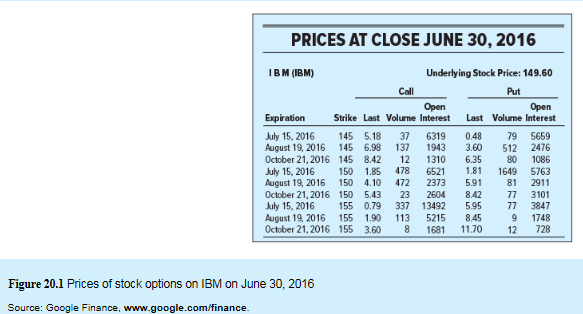
Let us calculate the payoff when Put option X is $145 and stock price on expiry date is $150.
| Calculation of payoff in case of a put option | ||
| Position | If Stock price is less than X | If Stock price is greater or equal to X |
| Payoff to Put holder | X-Stock price | 0 |
| Payoff to Put writer | -(X-Stock price) | 0 |
Stock price at expiration is $150.
Exercise or Strike price X=$145.
So, let us now substitute the values in the above table. We get
| Calculation of payoff in case of a put option | ||
| Position | If Stock price is less than X | If Stock price is greater or equal to X |
| Payoff to Put holder | $0 | 0 |
| Payoff to Put writer | $0 | 0 |
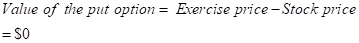
But, we are informed that the put option is $0.48 at a strike price of $145 on June2016.
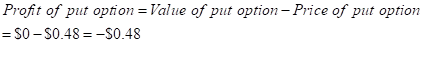
Therefore, the loss incurred by the buyer on put option will be -$0.48.
c
To compute: The payoff and the profit for investments when the call option’s exercise price X=$150 assuming that the stock price on the expiration date is $150.
Introduction:
Profit on investment: Investments are supposed to be considered as a monetary asset. Investments are done with an expectation to earn good income in future or to sell this asset at a higher price. If the purchase price of the asset is less than the sale price of the asset, it can be termed as profit on investment else it is loss on investment.
c
Answer to Problem 5PS
The call buyer will incur loss of -$1.85 when the exercise price is $150.
Explanation of Solution
The information given to us is as follows:
Let us calculate the payoff when Call option X is $150 and stock price on expiry date is $150.
| Calculation of payoff in case of call option: | ||
| Position | Stock price > X | Stock price is less than or equal to X |
| Payoff to call holder | Stock price -X | 0 |
| Payoff to call writer | -(Stock price -X) | 0 |
Stock price at expiration is $150.
Exercise or Strike price X=$150.
So, let us now substitute the values in the above table. We get
| Calculation of payoff in case of call option | ||
| Position | Stock price > X | Stock price is less than or equal to X |
| Payoff to call holder | 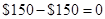 | 0 |
| Payoff to call writer | 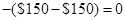 | 0 |
By the above calculation, it is observed that the call writer is prepared to bear the risk in return of option premium as there is loss if stock price increases.
Calculation of profit for investment:

But as per the information given to us, the price of the call option is $1.85 at a strike price $150 on June 2016.
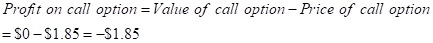
Therefore, the call buyer will incur loss of -$1.85.
d.
To compute: The payoff and the profit for investments when the put option’s exercise price X=$150 assuming that the stock price on the expiration date is $150.
Introduction:
Options: Options are the instruments used in financial transactions. These are derived based on the value of the underlying assets. Normally, the purpose of an option is to provide the buyer an opportunity to buy or sell the underlying asset depending upon the type of contract they possess. There are two types of options- Call option and put option.
d.
Answer to Problem 5PS
The incurred by the put buyer will be -$1.81 when the exercise price is $150.
Explanation of Solution
The information given to us is as follows:
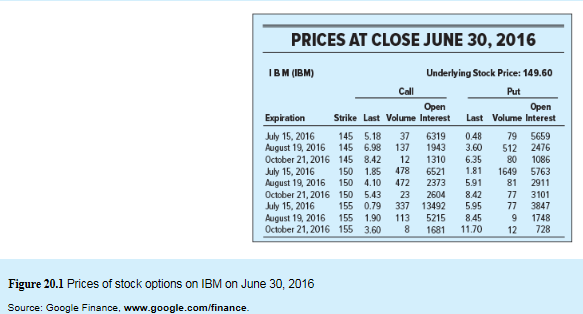
Let us calculate the payoff when Put option X is $150 and stock price on expiry date is $150.
| Calculation of payoff in case of a put option | ||
| Position | If Stock price is less than X | If Stock price is greater or equal to X |
| Payoff to Put holder | X-Stock price | 0 |
| Payoff to Put writer | -(X-Stock price) | 0 |
Stock price at expiration is $150.
Exercise or Strike price X=$150.
So, let us now substitute the values in the above table. We get
| Calculation of payoff in case of a put option | ||
| Position | If Stock price is less than X | If Stock price is greater or equal to X |
| Payoff to Put holder | $0 | 0 |
| Payoff to Put writer | $0 | 0 |
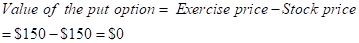
But, we are informed that the put option is $1.81 at a strike price of $150 on June 2016.
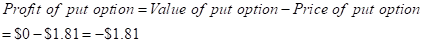
Therefore, the loss incurred by the buyer on put option will be -$1.81.
e.
To compute: The payoff and the profit for investments when the call option’s exercise price X=$155 assuming that the stock price on the expiration date is $150.
Introduction:
Payoff: In financial terminology, payoff refers to the return on an investment.
e.
Answer to Problem 5PS
The loss incurred by the call buyer will be -$0.79 when the exercise price is $155.
Explanation of Solution
The information given to us is as follows:
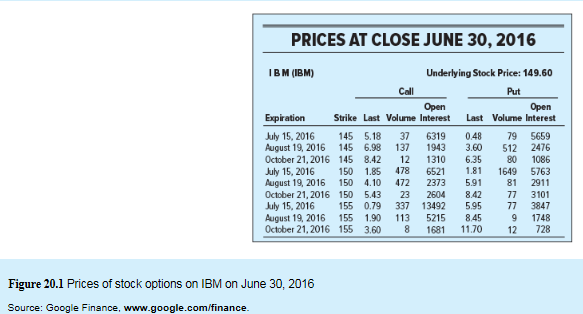
Let us calculate the payoff when Call option X is $155 and stock price on expiry date is $150.
| Calculation of payoff in case of call option | ||
| Position | Stock price > X | Stock price is less than or equal to X |
| Payoff to call holder | Stock price -X | 0 |
| Payoff to call writer | -(Stock price -X) | 0 |
Stock price at expiration is $150.
Exercise or Strike price X=$155.
So, let us now substitute the values in the above table. We get
| Calculation of payoff in case of call option | ||
| Position | Stock price > X | Stock price is less than or equal to X |
| Payoff to call holder | 0 | 0 |
| Payoff to call writer | 0 | 0 |
By the above calculation, it is observed that the call writer is prepared to bear the risk in return of option premium as there is loss if stock price increases.
Calculation of profit for investment
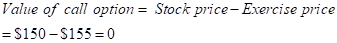
But as per the information given to us, the price of the call option is $0.79 at a strike price $155 on June 2016.
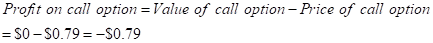
Therefore, the call buyer will incur loss of -$0.79.
f.
To compute: The payoff and the profit for investments when the put option’s exercise price X=$155 assuming that the stock price on the expiration date is $150.
Introduction:
Loss on investment: Investments are supposed to be considered as a monetary asset. Investments are done with an expectation to earn good income in future or to sell this asset at a higher price. If the purchase price of the asset is less than the sale price of the asset, it can be termed as profit on investment else it is loss on investment.
f.
Answer to Problem 5PS
The loss incurred by the put buyer will be $-0.95 when the exercise price is $155.
Explanation of Solution
The information given to us is as follows:

Let us calculate the payoff when Put option X is $155 and stock price on expiry date is $150.
| Calculation of payoff in case of a put option | ||
| Position | If Stock price is less than X | If Stock price is greater or equal to X |
| Payoff to Put holder | X-Stock price | 0 |
| Payoff to Put writer | -(X-Stock price) | 0 |
Stock price at expiration is $150.
Exercise or Strike price X=$155.
So, let us now substitute the values in the above table. We get
| Calculation of payoff in case of a put option | ||
| Position | If Stock price is less than X | If Stock price is greater or equal to X |
| Payoff to Put holder | 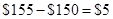 | 0 |
| Payoff to Put writer | 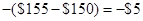 | 0 |
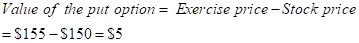
But, we are informed that the put option is $5.95 at a strike price of $155 on June 2016.
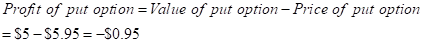
Therefore, the loss incurred by the buyer on put option will be -0.95.
Want to see more full solutions like this?
Chapter 20 Solutions
EBK INVESTMENTS
- Forest Enterprises, Incorporated, has been considering the purchase of a new manufacturing facility for $290,000. The facility is to be fully depreciated on a straight-line basis over seven years. It is expected to have no resale value after the seven years. Operating revenues from the facility are expected to be $125,000, in nominal terms, at the end of the first year. The revenues are expected to increase at the inflation rate of 2 percent. Production costs at the end of the first year will be $50,000, in nominal terms, and they are expected to increase at 3 percent per year. The real discount rate is 5 percent. The corporate tax rate is 25 percent. Calculate the NPV of the project. Note: Do not round intermediate calculations and round your answer to 2 decimal places, e.g., 32.16. NPVarrow_forwardHelp with questionsarrow_forwardPlease help with questionsarrow_forward
- Create financial forecasting years 2022, 2023, and 2024 using this balance sheet.arrow_forwardBeta Company Ltd issued 10% perpetual debt of Rs. 1,00,000. The company's tax rate is 50%. Determine the cost of capital (before tax as well as after tax) assuming the debt is issued at 10 percent premium. helparrow_forwardFinance subject qn solve.arrow_forward
 Essentials Of InvestmentsFinanceISBN:9781260013924Author:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.Publisher:Mcgraw-hill Education,
Essentials Of InvestmentsFinanceISBN:9781260013924Author:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.Publisher:Mcgraw-hill Education,

 Foundations Of FinanceFinanceISBN:9780134897264Author:KEOWN, Arthur J., Martin, John D., PETTY, J. WilliamPublisher:Pearson,
Foundations Of FinanceFinanceISBN:9780134897264Author:KEOWN, Arthur J., Martin, John D., PETTY, J. WilliamPublisher:Pearson, Fundamentals of Financial Management (MindTap Cou...FinanceISBN:9781337395250Author:Eugene F. Brigham, Joel F. HoustonPublisher:Cengage Learning
Fundamentals of Financial Management (MindTap Cou...FinanceISBN:9781337395250Author:Eugene F. Brigham, Joel F. HoustonPublisher:Cengage Learning Corporate Finance (The Mcgraw-hill/Irwin Series i...FinanceISBN:9780077861759Author:Stephen A. Ross Franco Modigliani Professor of Financial Economics Professor, Randolph W Westerfield Robert R. Dockson Deans Chair in Bus. Admin., Jeffrey Jaffe, Bradford D Jordan ProfessorPublisher:McGraw-Hill Education
Corporate Finance (The Mcgraw-hill/Irwin Series i...FinanceISBN:9780077861759Author:Stephen A. Ross Franco Modigliani Professor of Financial Economics Professor, Randolph W Westerfield Robert R. Dockson Deans Chair in Bus. Admin., Jeffrey Jaffe, Bradford D Jordan ProfessorPublisher:McGraw-Hill Education





