
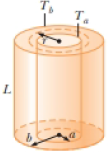
(a) The inside of a hollow cylinder is maintained at a temperature Ta, and the outside is at a lower temperature, Tb (Fig. P19.45). The wall of the cylinder has a thermal conductivity k. Ignoring end effects, show that the rate of energy
Suggestions: The temperature gradient is dT/dr. A radial energy current passes through a concentric cylinder of area 2πrL. (b) The passenger section of a jet airliner is in the shape of a cylindrical tube with a length of 35.0 m and an inner radius of 2.50 m. Its walls are lined with an insulating material 6.00 cm in thickness and having a thermal conductivity of 4.00 × 10−5 cal/s · cm · °C. A heater must maintain the interior temperature at 25.0°C while the outside temperature is −35.0°C. What power must be supplied to the heater?
Figure P19.45
Trending nowThis is a popular solution!

Chapter 20 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- An aluminum rod 0.500 m in length and with a cross sectional area of 2.50 cm2 is inserted into a thermally insulated vessel containing liquid helium at 4.20 K. The rod is initially at 3(H) K. (a) If one-halt of the rod is inserted into the helium, how many liters of helium boil off by the time the inserted half cools to 4.20 K? Assume the upper half does not yet cool, (b) If the circular surface of the upper end of the rod is maintained at 300 K. what is the approximate boil-off rate of liquid helium in liters per second after the lower half has reached 4.20 K? (Aluminum has thermal conductivity of 3 100 YV/m K at 4.20 K; ignore its temperature variation. The density of liquid helium is 125 kg/m3.)arrow_forwardHow many moles are there in (a) 0.0500 g of N2 gas (M = 28.0 g/mol)? (b) 10.0 g of CO2 gas (M = 44.0 g/mol)? (c) How many molecules are present in each case?arrow_forwardConsider an object with any one of the shapes displayed in Table 10.2. What is the percentage increase in the moment of inertia of the object when it is warmed from 0C to 100C if it is composed of (a) copper or (b) aluminum? Assume the average linear expansion coefficients shown in Table 16.1 do not vary between 0C and 100C. (c) Why are the answers for parts (a) and (b) the same for all the shapes?arrow_forward
- When builders were constructing a sidewalk they forgot to include an expansion joint between two of the segments, L = 2.1 m at To = 20° C. Assume the opposite ends of each segment are fixed and the linear expansion coefficient is α = 11 × 10-6 °C-1. a.) As the day heats to Tb the segments press against each other and begin to raise the junction a distance h forming a triangle. What is the height (in meters) at Tb=110° F? b.) What should the gap have been, in units of meters, to prevent them from touching?arrow_forwardIn a 60 mm diameter cylindrical nuclear reactor fuel rod ė ü, 1 = 3.929 × 107 W / m3 uniformly distributed There is heat generation and the temperature distribution in continuous regime is given by the equation T = a + br2. Here, A = 650 ° C and b = -3.274 x 105 ° C in T (° C) and r (m) units. The properties of the rod k = 30 W / m. K, p = 1100 kg / m3 and cp = 800 J/ kg · K: (a) What is the heat conduction (W 7 m) from the unit length of the rod at r = 0 (axis) and r = mm (surface)? (b) Reactor power level suddenly ė lf ü is increased to 2 = 108 W / m3, at r = 0 andr= be What is the change (@T / at) with time? 30 mm the temperature willarrow_forwardA walrus transfers energy by conduction through its blubber at the rate of 150 W when immersed in −1.00ºC water. The walrus’s internal core temperature is 37.0ºC , and it has a surface area of 2.00 m2 . What is the average thickness of its blubber, which has the conductivity of fatty tissues without blood?arrow_forward
- An isolated bar is kept at zero temperature at its ends. If it's given initially temperature, f(x) = 100°C, a2y equation u (x, t) is equal to: a2y so the bar temperature ax2 %3D u (0, t) u (L, t) [sin#x•e) , sin x -400 -400 (sinx-e ) + TC .x. (25x² sinx e sin x-e ) The Answer Is the Answer is O Isinx e e sin 400 None of all 3. 25m sin x earrow_forwardYou drop a 7 mole piece of zinc, which has been heated to 423 K into 0.101 kg of water at 300 K You can use equipartition for the zinc. Assume that the system (water+zinc) is completely isolated from the environment. The specific heat capacity of water is 4.186 J/g K. What is the change in temperature of the water? (a) 16.9 K (b) 175. K (c) 36.0 K (d) 50.8 K (e) 6.85 K ✔100% Did the entropy of the zinc increase, decrease or stay the same? (a) Increase (b) Decrease) (0) Stay the samearrow_forwardb) The heat capacity of solid lead oxide [PbO (s)] is given by Cp.m JK- mol = 44.35 – 1.47 × 10-32 Calculate the change in molar enthalpy (AHm) (in unit J mol*) of PbO (s) if it is cooled from 500 K to 300 K at constant pressure (P). Quantity Cp,m denotes molar heat capacity at constant pressure.arrow_forward
- I.C 02/A/ Use the Crank-Nicolson method to solve for the temperature distribution of a long thin rod with a length of 10 cm and the following values: k = 0.49 cal/(s cm °C), Ax = 2 cm, and At = st 0.1 s. Initially the temperature of the rod is 0°C and the boundary conditions are fixed for all times at 7(0, t) = 100°C and 7(10, t) = 50°C. Note that the rod is aluminum with C = 0.2174 cal/g °C) and p = 2.7 g/cm³. List the tridiagonal system of equations and determined the temperature up to 0.1 s.arrow_forwardAn insulated thermos contains of 200 cm3 of hot water at 90°C . A cube of copper at 10°C with density 8.9 g/cm3 is dropped into the water and reaches thermal equilibrium eventually. The mass of the copper is 100 g. The specific heat, and coefficient of linear expansion of copper are 0.39 Jg^-1°C^-1? and 17 × 10-6 C-1, respectively. The density and specific heat of water are 1.00 g/cm3 and 4.18 Jg^-1°C^-1 , respectively. (a) Determine the temperature of the copper after thermal equilibrium. (b) Calculate the heat absorbed by the copper. (c) Estimate the volume changed of the copper. (d) Estimate the density changed of the copper. Is the density increasing or decreasing compared to the density at 10°?? (e) Explain briefly how a thermos keeps your water warm.arrow_forwardRailroad tracks are made from segments L = 65 m long at T = 20° C. When the tracks are laid, the engineers leave gaps of width l between adjacent segments to allow for thermal expansion. The coefficient of linear expansion is α = 12 × 10-6 °C-1 and engineers design the tracks to withstand temperatures of Tc = 39.5 degrees. A) Enter an expression, in terms of given variables, for the minimum gap distance l the engineers must leave for a track rated at temperature Tc. l= B)What is the minimum gap distance in meters? C) Suppose the engineers forgot to add the gaps at the beginning of 15 segments. How much longer, in meters, would the track be at Tc?arrow_forward
 Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning





