Mastering Physics with Pearson eText -- Standalone Access Card -- for University Physics with Modern Physics (14th Edition)
14th Edition
ISBN: 9780133978216
Author: Hugh D. Young, Roger A. Freedman
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 20, Problem 20.39P
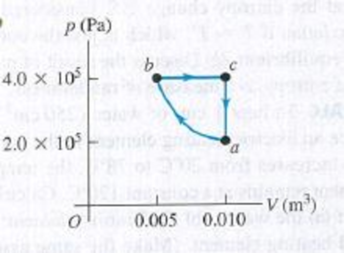
CALC You build a heal engine that takes 1.00 mol of an ideal diatomic gas through the cycle shown in Fig. P20.39. (a) Show that process ab is an isothermal compression. (b) During which process(es) of the cycle is heat absorbed by the gas? During which process(es) is heat rejected? How do you know? Calculate (c) the temperature at points a, b, and c; (d) the net heat exchanged with the surroundings and net work done by the engine in one cycle; (e) the thermal efficiency of the engine.
Figure P20.39
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 20 Solutions
Mastering Physics with Pearson eText -- Standalone Access Card -- for University Physics with Modern Physics (14th Edition)
Ch. 20.1 - Your left and right hands are normally at the same...Ch. 20.2 - Rank the following heat engines in order from...Ch. 20.3 - For an Otto-cycle engine with cylinders of a fixed...Ch. 20.4 - Can you cool your house by leaving the...Ch. 20.5 - Would a 100%-efficient engine (Fig. 20.11a)...Ch. 20.6 - An inventor looking for financial support comes to...Ch. 20.7 - Suppose 2.00 kg of water at 50C spontaneously...Ch. 20.8 - A quantity of N molecules of an ideal gas...Ch. 20 - A pot is half-filled with water, and a lid is...Ch. 20 - Prob. 20.2DQ
Ch. 20 - Prob. 20.3DQCh. 20 - Prob. 20.4DQCh. 20 - Why must a room air conditioner be placed in a...Ch. 20 - Prob. 20.6DQCh. 20 - Prob. 20.7DQCh. 20 - An electric motor has its shaft coupled to that of...Ch. 20 - When a wet cloth is hung up in a hot wind in the...Ch. 20 - Compare the pV-diagram for the Otto cycle in Fig....Ch. 20 - The efficiency of heat engines is high when the...Ch. 20 - What would be the efficiency of a Carnot engine...Ch. 20 - Real heat engines, like the gasoline engine in a...Ch. 20 - Does a refrigerator full of food consume more...Ch. 20 - In Example 20.4, a Carnot refrigerator requires a...Ch. 20 - How can the thermal conduction of heat from a hot...Ch. 20 - Explain why each of the following processes is an...Ch. 20 - The free expansion of an ideal gas is an adiabatic...Ch. 20 - Are the earth and sun in thermal equilibrium? Are...Ch. 20 - Prob. 20.20DQCh. 20 - Prob. 20.21DQCh. 20 - Prob. 20.22DQCh. 20 - BIO A growing plant creates a highly complex and...Ch. 20 - A diesel engine performs 2200 J of mechanical work...Ch. 20 - An aircraft engine takes in 9000 J of heat and...Ch. 20 - A Gasoline Engine. A gasoline engine takes in 1.61...Ch. 20 - A gasoline engine has a power output of 180 kW...Ch. 20 - The pV-diagram in Fig. E20.5 shows a cycle of heat...Ch. 20 - (a) Calculate the theoretical efficiency for an...Ch. 20 - The Otto-cycle engine in a Mercedes-Benz SL1 a...Ch. 20 - Section 20.4 Refrigerators 20.8The coefficient of...Ch. 20 - A refrigerator has a coefficient of performance of...Ch. 20 - A freezer has a coefficient of performance of...Ch. 20 - A refrigerator has a coefficient of performance of...Ch. 20 - A Carnot engine is operated between two heat...Ch. 20 - A Carnot engine whose high-temperature reservoir...Ch. 20 - An ice-making machine operates in a Carnot cycle....Ch. 20 - A Carnot engine has an efficiency of 66% and...Ch. 20 - A certain brand of freezer is advertised to use...Ch. 20 - A Carnot refrigerator is operated between two heat...Ch. 20 - A Carnot heat engine uses a hot reservoir...Ch. 20 - You design an engine that takes in 1.50 104 J of...Ch. 20 - A 4.50-kg block of ice at 0.00C falls into the...Ch. 20 - A sophomore with nothing better to do adds heat to...Ch. 20 - CALC You decide to take a nice hot bath but...Ch. 20 - A 15.0-kg block of ice at 0.0C melts to liquid...Ch. 20 - CALC You make tea with 0.250 kg of 85.0C water and...Ch. 20 - Three moles of an ideal gas undergo a reversible...Ch. 20 - What is the change in entropy of 0.130 kg of...Ch. 20 - (a) Calculate the change in entropy when 1.00 kg...Ch. 20 - Entropy Change Due to Driving. Premium gasoline...Ch. 20 - CALC Two moles of an ideal gas occupy a volume V....Ch. 20 - A box is separated by a partition into two parts...Ch. 20 - CALC A lonely party balloon with a volume of 2.40...Ch. 20 - You are designing a Carnot engine that has 2 mol...Ch. 20 - CP An ideal Carnot engine operates between 500C...Ch. 20 - Prob. 20.34PCh. 20 - CP A certain heat engine operating on a Carnot...Ch. 20 - A heat engine takes 0.350 mol of a diatomic ideal...Ch. 20 - Prob. 20.37PCh. 20 - What is the thermal efficiency of an engine that...Ch. 20 - CALC You build a heal engine that takes 1.00 mol...Ch. 20 - CP As a budding mechanical engineer, you are...Ch. 20 - CALC A heal engine Operates using the cycle shown...Ch. 20 - CP BIO Humun Entropy. A person who has skin of...Ch. 20 - An experimental power plant at the Natural Energy...Ch. 20 - CP BIO A Human Engine. You decide to use your body...Ch. 20 - CALC A cylinder contains oxygen at a pressure of...Ch. 20 - A monatomic ideal gas it taken around the cycle...Ch. 20 - A Carnot engine operates between two heat...Ch. 20 - A typical coal-fired power plant generates 1000 MW...Ch. 20 - Automotive Thermodynamics. A Volkswagen Passat has...Ch. 20 - An air conditioner operates on 800 W of power and...Ch. 20 - The pV-diagram in Fig. P20.51 shows the cycle for...Ch. 20 - BIO Human Entropy. A person with skin of surface...Ch. 20 - CALC An object of mass m1, specific heat c1, and...Ch. 20 - CALC To heat 1 cup of water (250 cm3) to make...Ch. 20 - DATA In your summer job with a venture capital...Ch. 20 - DATA For a refrigerator or air conditioner, the...Ch. 20 - DATA You are conducting experiments to study...Ch. 20 - Consider a Diesel cycle that starts (at point a in...Ch. 20 - POWER FROM THE SEA. Ocean thermal energy...Ch. 20 - POWER FROM THE SEA. Ocean thermal energy...Ch. 20 - POWER FROM THE SEA. Ocean thermal energy...Ch. 20 - POWER FROM THE SEA. Ocean thermal energy...
Additional Science Textbook Solutions
Find more solutions based on key concepts
A plank, fixed to a sled at rest in frame S, is of length L0 and makes an angle of 0 with the xaxis. Later, the...
Modern Physics
Choose the best answer to each of the following. Explain your reasoning. If we see a nova, we know that we are ...
Cosmic Perspective Fundamentals
Choose the best answer to each of the following. Explain your reasoning. The outer layer of most Jovian moons a...
The Cosmic Perspective Fundamentals (2nd Edition)
What effect does condensation on a glass of ice water have on the rate at which the ice melts? Will the condens...
College Physics
3. What is free-fall, and why does it make you weightless? Briefly describe why astronauts are weightless in th...
The Cosmic Perspective
The amount of charge passes through the battery during the start.
Physics (5th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A 1.00-mol sample of an ideal monatomic gas is taken through the cycle shown in Figure P18.63. The process AB is a reversible isothermal expansion. Calculate (a) the net work done by the gas, (b) the energy added to the gas by heat, (c) the energy exhausted from the gas by heat, and (d) the efficiency of the cycle. (e) Explain how the efficiency compares with that of a Carnot engine operating between the same temperature extremes. Figure P18.63arrow_forwardOf the following, which is not a statement of the second law of thermodynamics? (a) No heat engine operating in a cycle can absorb energy from a reservoir and use it entirely to do work, (b) No real engine operating between two energy reservoirs can be more efficient than a Carnot engine operating between the same two reservoirs, (c) When a system undergoes a change in state, the change in the internal energy of the system is the sum of the energy transferred to the system by heat and the work done on the system, (d) The entropy of the Universe increases in all natural processes, (e) Energy will not spontaneously transfer by heat from a cold object to a hot object.arrow_forwardAt point A in a Carnot cycle, 2.34 mol of a monatomic ideal gas has a pressure of 1 4000 kPa, a volume of 10.0 L, and a temperature of 720 K. The gas expands isothermally to point B and then expands adiabatically to point C, where its volume is 24.0 L. An isothermal compression brings it to point D, where its volume is 15.0 L. An adiabatic process returns the gas to point A. (a) Determine all the unknown pressures, volumes, and temperatures as you f ill in the following table: (b) Find the energy added by heat, the work done by the engine, and the change in internal energy for each of the steps A B, B C, C D, and D A (c) Calculate the efficiency Wnet/|Qk|. (d) Show that the efficiency is equal to 1 - TC/TA, the Carnot efficiency.arrow_forward
- A Carnot engine employs 1.5 mol of nitrogen gas as a working substance, which is considered as an ideal diatomic gas with =7.5 at the working temperatures of the engine. The Carnot cycle goes in the cycle ABCDA with AB being an isothermal expansion. The volume at points A and C of the cycle are 5.0103 m3 and 0.15 L, respectively. The engine operates between two thermal baths of temperature 500 K 300 K. (a) Find the values of volume at B and D. (b) How much heat is absorbed by the gas in the AB isothermal expansion? (c) How much work is done by the gas in the AB isothermal expansion? (d) How much heat is given up by the gas in the CD isothermal expansion? (e) How much work is done by the gas in the CD isothermal compression? (f) How much work is done by the gas in the BC adiabatic expansion? (g) How much work is done by the gas in the DA adiabatic compression? (h) Find the value of efficiency of the engine based on the net and heat input. Compare this value to the efficiency of a Carnot engine based on the temperatures of the baths.arrow_forwardA car salesperson claims that a 300-hp engine is a necessary option in a compact car, in place of the conventional 130-hp engine. Suppose you intend to drive the car within speed limits ( 65 mi/h) on flat terrain. How would you counter this sales pitch?arrow_forwardAs shown below, calculate the work done by the gas in the quasi-static processes represented by the paths (a) AB; (b) ADB; (c) ACB; and (d) ADCB. `arrow_forward
- Use a PV diagram such as the one in Figure 22.2 (page 653) to figure out how you could modify an engine to increase the work done.arrow_forwardAn ideal gas with specific heat ratio confined to a cylinder is put through a closed cycle. Initially, the gas is at Pi, Vi, and Ti. First, its pressure is tripled under constant volume. It then expands adiabatically to its original pressure and finally is compressed isobarically to its original volume. (a) Draw a PV diagram of this cycle. (b) Determine the volume at the end of the adiabatic expansion. Find (c) the temperature of the gas at the start of the adiabatic expansion and (d) the temperature at the end of the cycle. (e) What was the net work done on the gas for this cycle?arrow_forward(a) Determine the work done on a gas that expands from i to f as indicated in Figure P19.16. (b) What If? How much work is done on the gas if it is compressed from f to i along the same path? Figure P19.16arrow_forward
- Figure P21.45 shows a cyclic process ABCDA for 1.00 mol of an ideal gas. The gas is initially at Pi = 1.50 105 Pa, Vi = 1.00 103 m3 (point A in Fig. P21.45). a. What is the net work done on the gas during the cycle? b. What is the net amount of energy added by heat to this gas during the cycle? FIGURE P21.45arrow_forward(a) What is the hot reservoir temperature of a Carnot engine that has an eficiency of 42.0% and a cold reservoir temperature of 210C ? (b) What must the hot reservoir temperature be for a real heat engine that achieves 0.700 of the maximum eficiency, but still has an efficiency of 42.0% (and a cold reservoir at 27.0C )? (c) Does your answer imply practical limits to the efficiency of car gasoline engines?arrow_forward(a) How much heat transfer occurs from 20.0 kg of 90.0C water placed in contact with 20.0 kg of 10.0C water, producing a final temperature of 50.0C ? (b) How much work could a Carnot engine do with this heat transfer, assuming it operates between two reservoirs at constant temperatures of 90.0C and 10.0C ? (c) What increase in entropy is produced by mixing 20.0 kg of 90.0C water with 20.0 kg of 10.0C water? (d) Calculate the amount of work made unavailable by this mixing using a low temperature of 10.0C, and compare it with the work done by the Garnet engine. Explicitly show how you follow the steps in the Problem-Solving Strategies for Entropy. (e) Discuss how everyday processes make increasingly more energy unavailable to do work, as implied by this problem.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
The Second Law of Thermodynamics: Heat Flow, Entropy, and Microstates; Author: Professor Dave Explains;https://www.youtube.com/watch?v=MrwW4w2nAMc;License: Standard YouTube License, CC-BY