
House freshmen: Newly elected members of the U.S. House of Representatives are referred to as “freshmen.” The following frequency distribution presents the number of freshmen elected in each of the past 53 elections, from 1912 to 2016.

- How many classes are there?
- What is the class width?
- What are the class limits?
- Construct a frequency histogram.
- Construct a relative frequency distribution.
- Construct a relative frequency histogram.
- In what percentage of elections were loo or more freshmen elected?
- In what percentage of elections were fewer than 60 freshmen elected?
a.
To find:Number of classes.
Answer to Problem 6RE
The number of classes is 8.
Explanation of Solution
Given information:The following frequency distribution presents the numberof freshmen elected in each of the past 53 elections from 1912 to 2016.
| Number of Freshmen | Frequency |
| 20-39 | 2 |
| 40-59 | 15 |
| 60-79 | 10 |
| 80-99 | 14 |
| 100-119 | 7 |
| 120-139 | 3 |
| 140-159 | 1 |
| 160-179 | 1 |
Calculation:
The classes from the given table are 20-39, 40-59, 60-79, 80-99, 100-119, 120-139, 140-159 and 160-179.
There are eight classes are there.
Hence, the number of classes is 8.
b.
To find: The class width.
Answer to Problem 6RE
The class width is 19.
Explanation of Solution
Given information: The following frequency distribution presents the number of freshmen elected in each of the past 53 elections from 1912 to 2016.
| Number of Freshmen | Frequency |
| 20-39 | 2 |
| 40-59 | 15 |
| 60-79 | 10 |
| 80-99 | 14 |
| 100-119 | 7 |
| 120-139 | 3 |
| 140-159 | 1 |
| 160-179 | 1 |
Formula used:
Calculation:
From the given table, the largest value is 179 and the smallest value is 20.
The number of classes is 8.
Then the class width is given by
Hence, the class width is 19.
c.
To find: The class limits.
Answer to Problem 6RE
The lower class limits are 20, 40, 60, 80, 100, 120, 140 and 160.
The upper class limits are 39, 59, 79, 99, 119, 139, 159 and 179.
Explanation of Solution
Given information: The following frequency distribution presents the number of freshmen elected in each of the past 53 elections from 1912 to 2016.
| Number of Freshmen | Frequency |
| 20-39 | 2 |
| 40-59 | 15 |
| 60-79 | 10 |
| 80-99 | 14 |
| 100-119 | 7 |
| 120-139 | 3 |
| 140-159 | 1 |
| 160-179 | 1 |
Definition used:
The lower class limits of a class are the smallest value that can appear in that class.
The upper class limits of a class are the largest value that can appear in that class.
Calculation:
From the given table we can say that
The lower class limits are 20, 40, 60, 80, 100, 120, 140 and 160.
The upper class limits are 39,59, 79, 99, 119, 139, 159 and 179.
d.
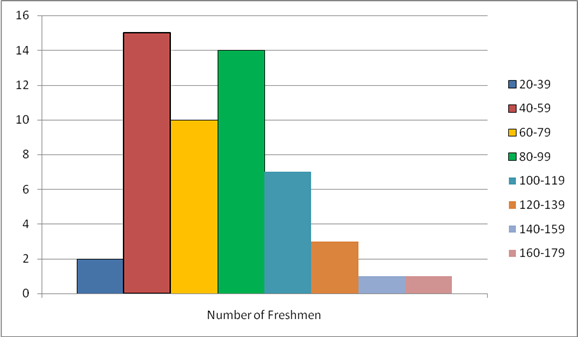
To construct: A frequency histogram.
Explanation of Solution
Given information: The following frequency distribution presents the number of freshmen elected in each of the past 53 elections from 1912 to 2016.
| Number of Freshmen | Frequency |
| 20-39 | 2 |
| 40-59 | 15 |
| 60-79 | 10 |
| 80-99 | 14 |
| 100-119 | 7 |
| 120-139 | 3 |
| 140-159 | 1 |
| 160-179 | 1 |
Definition used:
Histogram based on frequency is called frequency histogram.
Solution:
From the given table, the frequency histogram is given by
e.
To construct: The relative frequency distribution.
Explanation of Solution
Given information: The following frequency distribution presents the number of freshmen elected in each of the past 53 elections from 1912 to 2016.
| Number of Freshmen | Frequency |
| 20-39 | 2 |
| 40-59 | 15 |
| 60-79 | 10 |
| 80-99 | 14 |
| 100-119 | 7 |
| 120-139 | 3 |
| 140-159 | 1 |
| 160-179 | 1 |
Formula used:
Calculation:
From the given table,
The sum of all frequency is
The table of relative frequency is given by
| Number of Freshmen | Frequency | Relative Frequency |
| 20-39 | 2 | |
| 40-59 | 15 | |
| 60-79 | 10 | |
| 80-99 | 14 | |
| 100-119 | 7 | |
| 120-139 | 3 | |
| 140-159 | 1 | |
| 160-179 | 1 |
f.
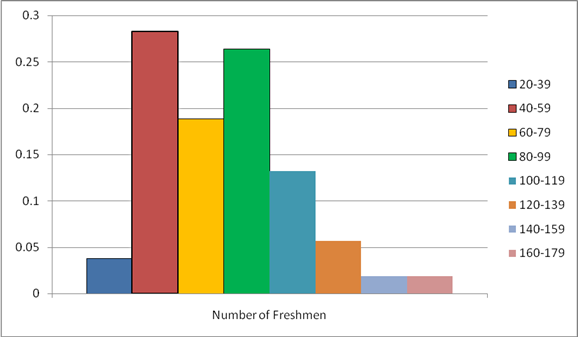
To construct: A relative frequency histogram.
Explanation of Solution
Given information: The following frequency distribution presents the number of freshmen elected in each of the past 53 elections from 1912 to 2016.
| Number of Freshmen | Frequency |
| 20-39 | 2 |
| 40-59 | 15 |
| 60-79 | 10 |
| 80-99 | 14 |
| 100-119 | 7 |
| 120-139 | 3 |
| 140-159 | 1 |
| 160-179 | 1 |
Definition used:
Histogram based on relative frequency is called relative frequency histogram.
Solution:
| Number of Freshmen | Frequency | Relative Frequency |
| 20-39 | 2 | |
| 40-59 | 15 | |
| 60-79 | 10 | |
| 80-99 | 14 | |
| 100-119 | 7 | |
| 120-139 | 3 | |
| 140-159 | 1 | |
| 160-179 | 1 |
From the above table, the relative frequency histogram is given by
g.
To find: The percentage of elections was 100 or more freshmen elected.
Answer to Problem 6RE
The percentage of elections was 100 or more freshmen elected is
Explanation of Solution
Given information: The following frequency distribution presents the number of freshmen elected in each of the past 53 elections from 1912 to 2016.
| Number of Freshmen | Frequency |
| 20-39 | 2 |
| 40-59 | 15 |
| 60-79 | 10 |
| 80-99 | 14 |
| 100-119 | 7 |
| 120-139 | 3 |
| 140-159 | 1 |
| 160-179 | 1 |
Definition used:
Percentage for a frequency is given by
Calculation:
From the given table we can say that
The frequency for 100 or more freshmen elected is 7, 3, 1 and 1.
The sum of all frequencies of 100 or more freshmen were elected is
The sum of all frequency is 53.
Hence, the percentage is given by
Hence, the percentage of elections was 100 or more freshmen electedis
h.
To find: The percentage of elections was fewer than 60 freshmen elected.
Answer to Problem 6RE
Thepercentage of elections was fewer than 60 freshmen elected is
Explanation of Solution
Given information: The following frequency distribution presents the number of freshmen elected in each of the past 53 elections from 1912 to 2016.
| Number of Freshmen | Frequency |
| 20-39 | 2 |
| 40-59 | 15 |
| 60-79 | 10 |
| 80-99 | 14 |
| 100-119 | 7 |
| 120-139 | 3 |
| 140-159 | 1 |
| 160-179 | 1 |
Definition used:
Percentage for a frequency is given by
Calculation:
From the given table we can say that
The frequency for fewer than 60 freshmen elected is 2 and 15.
The sum of all frequencies of fewer than 60 freshmen were elected is
The sum of all frequency is 53.
Hence, the percentage is given by
Hence, the percentage of elections was fewer than 60 freshmen elected is
Want to see more full solutions like this?
Chapter 2 Solutions
Elementary Statistics
- 2PM Tue Mar 4 7 Dashboard Calendar To Do Notifications Inbox File Details a 25/SP-CIT-105-02 Statics for Technicians Q-7 Determine the resultant of the load system shown. Locate where the resultant intersects grade with respect to point A at the base of the structure. 40 N/m 2 m 1.5 m 50 N 100 N/m Fig.- Problem-7 4 m Gradearrow_forwardNsjsjsjarrow_forwardA smallish urn contains 16 small plastic bunnies - 9 of which are pink and 7 of which are white. 10 bunnies are drawn from the urn at random with replacement, and X is the number of pink bunnies that are drawn. (a) P(X=6)[Select] (b) P(X>7) ≈ [Select]arrow_forward
- A smallish urn contains 25 small plastic bunnies - 7 of which are pink and 18 of which are white. 10 bunnies are drawn from the urn at random with replacement, and X is the number of pink bunnies that are drawn. (a) P(X = 5)=[Select] (b) P(X<6) [Select]arrow_forwardElementary StatisticsBase on the same given data uploaded in module 4, will you conclude that the number of bathroom of houses is a significant factor for house sellprice? I your answer is affirmative, you need to explain how the number of bathroom influences the house price, using a post hoc procedure. (Please treat number of bathrooms as a categorical variable in this analysis)Base on the same given data, conduct an analysis for the variable sellprice to see if sale price is influenced by living area. Summarize your finding including all regular steps (learned in this module) for your method. Also, will you conclude that larger house corresponding to higher price (justify)?Each question need to include a spss or sas output. Instructions: You have to use SAS or SPSS to perform appropriate procedure: ANOVA or Regression based on the project data (provided in the module 4) and research question in the project file. Attach the computer output of all key steps (number) quoted in…arrow_forwardElementary StatsBase on the given data uploaded in module 4, change the variable sale price into two categories: abovethe mean price or not; and change the living area into two categories: above the median living area ornot ( your two group should have close number of houses in each group). Using the resulting variables,will you conclude that larger house corresponding to higher price?Note: Need computer output, Ho and Ha, P and decision. If p is small, you need to explain what type ofdependency (association) we have using an appropriate pair of percentages. Please include how to use the data in SPSS and interpretation of data.arrow_forward
- An environmental research team is studying the daily rainfall (in millimeters) in a region over 100 days. The data is grouped into the following histogram bins: Rainfall Range (mm) Frequency 0-9.9 15 10 19.9 25 20-29.9 30 30-39.9 20 ||40-49.9 10 a) If a random day is selected, what is the probability that the rainfall was at least 20 mm but less than 40 mm? b) Estimate the mean daily rainfall, assuming the rainfall in each bin is uniformly distributed and the midpoint of each bin represents the average rainfall for that range. c) Construct the cumulative frequency distribution and determine the rainfall level below which 75% of the days fall. d) Calculate the estimated variance and standard deviation of the daily rainfall based on the histogram data.arrow_forwardAn electronics company manufactures batches of n circuit boards. Before a batch is approved for shipment, m boards are randomly selected from the batch and tested. The batch is rejected if more than d boards in the sample are found to be faulty. a) A batch actually contains six faulty circuit boards. Find the probability that the batch is rejected when n = 20, m = 5, and d = 1. b) A batch actually contains nine faulty circuit boards. Find the probability that the batch is rejected when n = 30, m = 10, and d = 1.arrow_forwardTwenty-eight applicants interested in working for the Food Stamp program took an examination designed to measure their aptitude for social work. A stem-and-leaf plot of the 28 scores appears below, where the first column is the count per branch, the second column is the stem value, and the remaining digits are the leaves. a) List all the values. Count 1 Stems Leaves 4 6 1 4 6 567 9 3688 026799 9 8 145667788 7 9 1234788 b) Calculate the first quartile (Q1) and the third Quartile (Q3). c) Calculate the interquartile range. d) Construct a boxplot for this data.arrow_forward
- Pam, Rob and Sam get a cake that is one-third chocolate, one-third vanilla, and one-third strawberry as shown below. They wish to fairly divide the cake using the lone chooser method. Pam likes strawberry twice as much as chocolate or vanilla. Rob only likes chocolate. Sam, the chooser, likes vanilla and strawberry twice as much as chocolate. In the first division, Pam cuts the strawberry piece off and lets Rob choose his favorite piece. Based on that, Rob chooses the chocolate and vanilla parts. Note: All cuts made to the cake shown below are vertical.Which is a second division that Rob would make of his share of the cake?arrow_forwardThree players (one divider and two choosers) are going to divide a cake fairly using the lone divider method. The divider cuts the cake into three slices (s1, s2, and s3). If the choosers' declarations are Chooser 1: {s1 , s2} and Chooser 2: {s2 , s3}. Using the lone-divider method, how many different fair divisions of this cake are possible?arrow_forwardTheorem 2.6 (The Minkowski inequality) Let p≥1. Suppose that X and Y are random variables, such that E|X|P <∞ and E|Y P <00. Then X+YpX+Yparrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt


